基于證據推理的有限理性風險型多屬性決策

夏夢頤，王應明

（福州大學經濟與管理學院，福州 350108）

風險型多屬性決策是指擁有多種自然狀態且不同自然狀態下各方案的屬性值各不相同的復雜型決策。當不確定性越來越多時，對各個屬性值的描述也逐漸變得模糊，不僅存在諸如年產值的精確數據，還存在區間數據和語言評價數據，而數據的多樣性加重了風險型決策的難度。直覺模糊數利用隸屬度、非隸屬度和猶豫度，可以較好地規范不同種類的數據并保留數據的不確定性。陳幗鸞等［1］將混合評價信息轉化為直覺模糊數，建立了優化模型并引入VIKOR理論對群決策問題進行評價排序。俞錦濤等［2］綜合直覺模糊集和猶豫模糊集的優點，給出了猶豫直覺模糊集的相關系數計算式，并將其運用到多屬性決策中。樂琦等［3］提出新的直覺模糊集排序函數，將其應用于雙邊匹配的問題。可見，直覺模糊數在處理風險型多屬性決策基礎數據上具有較大優勢。

早期的風險型多屬性決策方法是基于期望效用理論得到相應決策結果，認為決策者是完全理性的。然而，由于環境的復雜性與不確定性，在現實生活中的決策者往往是有限理性的。為此，Tversky等［4］提出了前景理論來描述決策者有限理性，這在一定程度上推動了風險型多屬性決策方法的發展。高建偉等［5］定義新的記分函數并運用前景理論對決策信息進行整合。朱麗等［6］定義了猶豫模糊元和區間猶豫模糊元的比較方法，運用前景理論對方案進行計算排序。糜萬俊等［7］運用方差分析原理構建群決策參考點，給出各類模糊數的價值函數計算方法，并將其應用于風險型多準則群決策。但上述文獻存在兩方面問題：第一，屬性權重固定為決策者的期望值，忽略了屬性值的客觀性，導致決策結果不符合客觀現實；第二，在對前景決策值進行合成時采用簡單加權原則，這在一定程度上容易造成信息丟失，無法高效集結不確定信息。

在決策信息集結方面，證據推理能夠較好地集結不確定信息，克服簡單加權原則存在的缺陷。證據推理由證據理論［8］發展而來，經過 Yang等［9-12］學者的研究逐漸成熟，被廣泛應用于應急決策［13］、軍事［14］、供應鏈［15］等領域。因證據推理方法擁有較強的優越性和包容性，一些學者也將其用于解決風險型多屬性決策問題。靳留乾等［16］利用確定因子結構表示不確定信息，再結合證據推理方法和第3代前景理論，解決不確定性多屬性決策問題。張美璟等［17］運用證據推理集結區間不確定評估信息并結合累計前景理論對不同方案進行決策。因此，將證據推理方法應用到風險型決策中可以有效防止決策過程中的信息流失，使決策結果更加符合客觀實際。

綜上所述，風險型多屬性決策方法在數據處理、權重確定、信息集結等方面仍具有改進空間，本文利用直覺模糊集、前景理論和證據推理等方法，對上述方面進行優化提升。

1 問題描述

2 決策方法

2.1 數據的整理與轉化

考慮決策數據含有精確值、區間值和語言值3種情況，為了避免不同量綱對決策結果產生影響，采用極差變換法先將精確數和區間數進行規范化［18］，規范化后的屬性值記為

定義 1［19］假設一個直覺模糊集 α=該式的含義可表述為非空集合Φ中有元素x屬于α，且其隸屬度為μα（x），非隸屬度為 να（x），猶豫度為 πα（x）=1-μα（x）-να（x），其中 μα∶Φ→ [0，]1，να∶Φ→[0，]1，且必須滿足 0≤μα（x）+να（x）≤1，?x∈Φ。μα（x）和 να（x）組成的有序對（μα（x），να（x））稱為直覺模糊數。

對于Cj∈CR，通過式（3）將ˉxtij轉化為直覺模糊數。由精確數的定義可知不存在猶豫度，即

對于Cj∈CL，可參照十一元語言短語集來確定具體語言評價等級對應的直覺模糊數［20］。十一元語言短語集見表1。

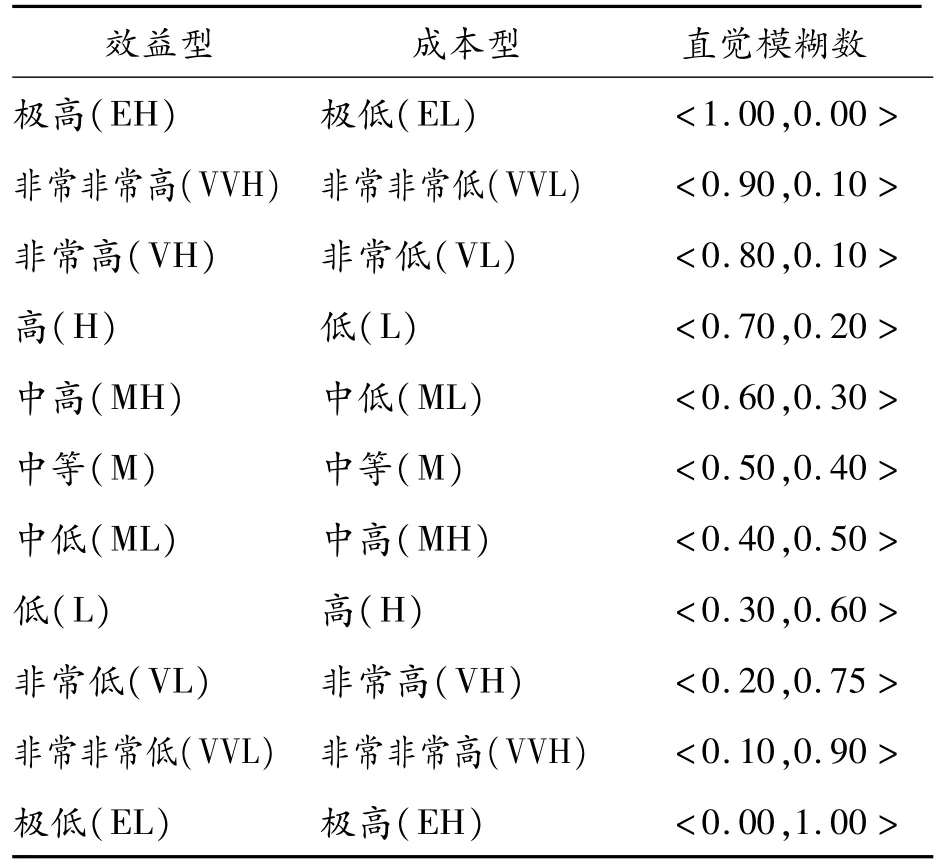
表1 十一元語言短語集

2.2 前景決策矩陣的生成

定義 2［4］Tversky和 Kahneman確定了前景理論的價值函數表達式是一個考慮與參考點距離的冪函數，表達式為

其中：Δx表示x偏離參考點的距離大小，Δx≥0是收益；α表示決策者面臨收益時的敏感性程度；Δx＜0是損失；θ是損失規避系數，表示面對損失時，決策者更加敏感；β表示決策者面臨損失時的敏感性程度。0≤α≤1，0≤β≤1，θ＞1。

Gonzalez等［21］給出了相應的概率權重函數，表達式為

其中：τ是權重函數的曲率，表示對概率差異的敏感性；δ是權重函數的仰角，表示對風險的偏好。

以決策者給出的期望向量為參考點進行前景值計算，記參考點的直覺模糊矩陣為

定義 3［22］設任意直覺模糊數 α=｛〈x，

為直覺模糊數的記分函數。其中HI=HI；

新的記分函數具有明顯優勢，不僅考慮了猶豫度π的作用，完善了Chen等［23］提出的原始記分函數，而且新的記分函數彌補了現有其他記分函數的缺點，引入了決策者的從眾心理，利用模糊交叉熵來確定猶豫度分配。記分函數值越大，表示決策者越滿意。

定義4［24］設有直覺模糊數 α=｛〈x，μα（x），να（x）〉|x∈Φ｝，λ＞0是任意實數，則運算法則如下：

2.3 屬性權重值的優化

張毛銀等［26］引入核概念得到新的直覺模糊熵計算公式，克服了以往各類直覺模糊熵存在的缺陷。計算St狀態下屬性Cj的直覺模糊熵Etj，直覺模糊熵Etj越小，說明數據越可靠。

2.4 前景值的融合

定義 6［8］設 Θ為識別框架，則函數 m∶2Θ→［0，1］滿足：① m（φ）=0；②m為Θ上的基本可信度分配（BPA），簡稱mass函數，A為Θ中的任意子集。其中，使m（A）＞0的A稱為焦元。

定義7［11］證據推理法中，設有n個評價等級構成辨識框架Θ，記為各個屬性是決策問題方案集中的證據，記為ei（i=1，2，…，I）。則證據 ei的評價結果可表示為

其中βn，i表示表示證據ei被評為等級Hn的置信度，，表示決策過程是完全確定的；當，表示決策過程存在不確定性，可表示為

結合證據推理融合公式，將所有屬性進行融合：

可得到St狀態下方案Ai的綜合前景值，為，其中不確定性表示

將融合信息進行整理得到St狀態下方案Ai的前景值

結合給出的狀態t發生的概率Pt，運用式（6）計算出現不同自然狀態St的概率權重值ω（pt），再次利用式（16）～（25）對決策數據進行二次融合，得到方案 Ai的綜合前景值其中

最后，利用式（7），計算出每個方案的記分函數，比較大小并進行排序，篩選出最佳方案。

3 算例分析

2018年，國家針對制造業相關企業頒布了減稅降費政策，持續推進去產能工作，放寬了一般制造業市場準入門檻，拓展了市場投資空間。其中新興產業、高技術類的制造業投資增速較快。在制造業增速發展的大環境下，某投資商擬選擇同一行業的5家制造企業 A1，A2，…，A5中的1家進行投資。主要從4個屬性對企業進行考察：年產值C1（千萬元）、社會收益（千萬元）、環境污染C3=｛EH，VVH，…，EL｝、企業規模 C4（千人）。其中，C1，C2，C4為效益型屬性，C3為成本型屬性，且C1是精確數，C2是直覺模糊數，C3是語言值，C4是區間值。根據以往的產業發展和投資經驗，屬性權重向量 ω=（0.3，0.2，0.3，0.2）且存在 3種市場狀態：好S1、中S2、差S3，發生概率分別是p1=0.3，p2=0.5，p3=0.2。此外，投資公司還給出了不同市場狀態下對不同屬性的期望值r1j=（3.0，［0.36，0.6］，M，［4.5，5.5］），r2j=（2.8，［0.32，0.45］，M，［3.0，3.7］），r3j=（2.5，［0.24，0.25］，M，［2.7，3.5］）。5家制造企業在不同市場狀態下的屬性值如表2所示。

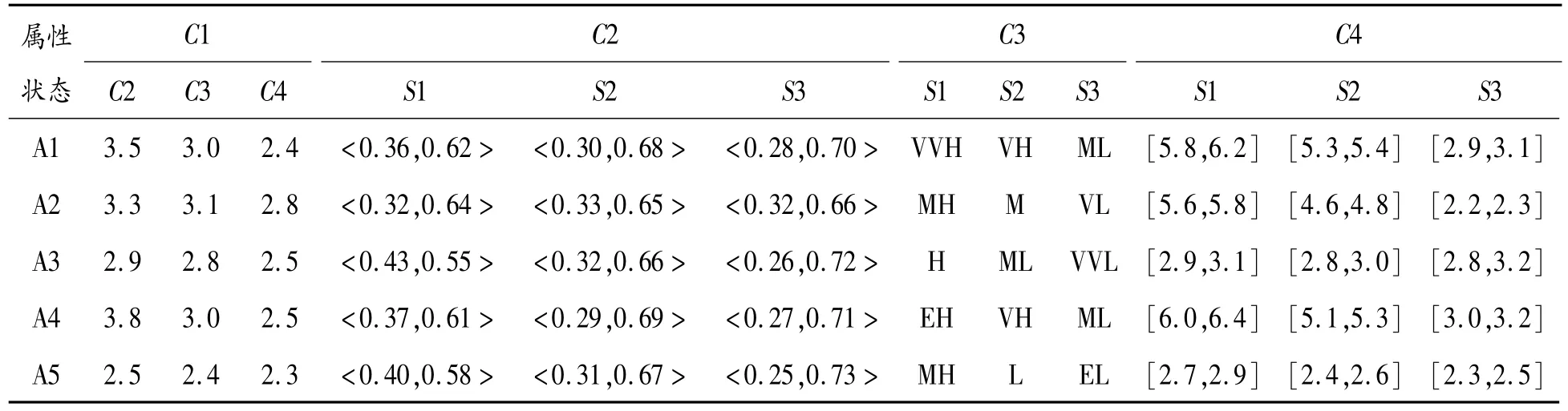
表2 不同市場狀態下5家制造企業的屬性值

步驟1 運用式（1）～（4）以及十一元語言短語集，將各屬性值規范化后轉化成對應的直覺模糊數

步驟2 將決策者給出的期望值作為參考點，運用式（8）（9）以及直覺模糊數的運算法則，求出前景決策矩陣，其中 α=β=0.88，θ=2.25。3種自然狀態下的結果為

步驟4 運用式（15）～（25）的證據推理方法，合成 St狀態下制造企業 Ai的前景值）。

步驟5 通過式（6）計算出不同自然狀態St的概率權重值 ω（pt）=（0.347，0.435，0.295）。參考文獻［6］中建議值δ=0.77，τ=0.44。再次運用式（15）～（25）的證據推理方法，合成綜合前景值

步驟6 運用定義3計算出每個制造企業記分函數為 S（A1）=0.645，S（A2）=0.738，S（A3）=0.666，S（A4）=0.531，S（A5）=0.463。5家制造企業的排序結果為A2＞A3＞A1＞A4＞A5。

根據文獻［5］中提出的方法，得到好、中、差這3種市場狀態下的記分函數S1，S2，S3。

最后，得到每個制造企業的綜合前景值為B（A1）=-0.332，B（A2）=0.108，B（A3）=-0.491，B（A4）=-0.264，B（A5）=-1.159。因此5家制造企業的排序結果為A2＞A4＞A1＞A3＞A5。采用文獻［5］方法與本文中方法的計算結果見表3。

表3 文獻［5］方法與本文中方法計算結果

通過對比發現企業3、4的排序位置發生變化，企業3、4的原始數據對比表明：雖然企業4年產在市場狀態好的情況下明顯高于企業3，但其在另外兩種市場狀態下的年產值與企業3差別不大，且通過對其他屬性數據對比發現，企業4在社會收益方面明顯低于企業3，環境污染高于企業3，所以對于綜合預估排序結果企業4應位于企業3之后。現有方法與本文方法產生差異的主要原因可以歸結為兩點：第一，文獻［5］將直覺模糊數直接轉化為記分函數，無法體現數據的不確定性，導致決策信息在集結過程中出現流失；第二，文獻［5］采用簡單加權原則計算綜合前景值，無法高效集結以直覺模糊數等為原始數據的不確定信息。綜上所述，本文方法考慮更為全面，得到的結果更符合客觀現實。

4 結論

1）借助直覺模糊數的兼容性對各類信息進行統一，保留了原始信息。

2）通過前景理論將決策信息與參考點進行比較計算，將決策者看成“有限理性人”，更加符合實際情況。

3）考慮直覺模糊熵和直覺模糊相似度，整合屬性的客觀性和決策者的主觀性，使屬性權重得到優化。

4）發揮證據推理的優越性，對前景決策信息進行融合，保證決策信息不流失。

5）利用新的記分函數對方案進行排序，評價更為客觀。算例分析驗證了本文方法的可行性，表明其具有實際應用價值。