基于負(fù)半熵 下半方差 近似偏度的投資組合模型及應(yīng)用

歐 攀，王 沁，段靜靜，周文浩

（西南交通大學(xué)數(shù)學(xué)學(xué)院，成都 611756）

在全球經(jīng)濟(jì)一體化的推進(jìn)下，中國(guó)金融市場(chǎng)的波動(dòng)日益加劇，金融風(fēng)險(xiǎn)也隨之不斷增加，因此對(duì)金融市場(chǎng)風(fēng)險(xiǎn)進(jìn)行度量和控制是非常有必要的。1952年Markowitz［1］以投資組合收益率的方差作為風(fēng)險(xiǎn)度量，提出了均值方差投資組合模型（mean variance portfolio model，M-V），開(kāi)創(chuàng)了投資組合量化風(fēng)險(xiǎn)的先例。我國(guó)證券市場(chǎng)歷史較短，存在不成熟性和多變性，如何在一定約束條件下得到最優(yōu)投資決策，進(jìn)一步修正M-V模型，使其應(yīng)用于我國(guó)證券市場(chǎng)，這在理論研究和實(shí)際應(yīng)用中都有重要意義。

均值 方差模型中方差作為風(fēng)險(xiǎn)度量指標(biāo)，既包含收益向下的波動(dòng)，也包含向上的波動(dòng)。而投資者在實(shí)際投資時(shí)，更關(guān)心資產(chǎn)收益低于預(yù)期收益的那部分風(fēng)險(xiǎn)，因此提出了下半方差風(fēng)險(xiǎn)度量方法。J.Bi［2］給出了均值半方差投資組合模型；Rui Pedro Brito［3］提出了下半方差和偏度雙目標(biāo)優(yōu)化的投資組合模型；Yan W［4］考慮在多期情況下建立了多周期下半方差投資組合模型；王延章［5］構(gòu)建了下半方差的債券投資組合模型；李慧敏［6］構(gòu)建了下半方差的地產(chǎn)投資組合模型。半方差模型中下半方差度量風(fēng)險(xiǎn)，只說(shuō)明了收益率的偏離方向，而未反映證券組合的損失具體大小。信息熵也代表一種不確定性，風(fēng)險(xiǎn)的本質(zhì)是回報(bào)的不確定性。近年來(lái)很多學(xué)者考慮用信息熵度量資產(chǎn)風(fēng)險(xiǎn)，Philippatos［7］首先將熵引入投資組合模型，用熵代替方差度量風(fēng)險(xiǎn)。其后，更多學(xué)者用熵作為風(fēng)險(xiǎn)度量方法，其中，王燦杰［8］建立了均值熵偏度模型；YU J R［9］在熵模型的基礎(chǔ)上增加收益預(yù)測(cè)；張鵬［10］構(gòu)建了具有熵約束的組合投資模型；吳文娣［11］建立了具有廣義熵約束的投資組合模型；李?lèi)?ài)忠［12］、Mehmet Aksarayl?［13］、宋燕玲［14］同時(shí)考慮方差和信息熵風(fēng)險(xiǎn)度量指標(biāo)，構(gòu)建了均值方差熵投資組合模型。

綜上所述，國(guó)內(nèi)外學(xué)者分別用方差、下半方差、信息熵度量組合資產(chǎn)風(fēng)險(xiǎn)，修正了均值方差模型，建立了多種投資組合模型。本文結(jié)合投資者更關(guān)注資產(chǎn)收益處于下跌的心理和信息熵的優(yōu)點(diǎn)，構(gòu)建了負(fù)半熵—下半方差 近似偏度投資組合模型，互補(bǔ)了這些方法單獨(dú)度量風(fēng)險(xiǎn)時(shí)存在的一些缺陷，使模型更具有效性和可行性。

1 模型的建立

1.1 M-V投資組合模型

M-V投資組合模型用方差度量風(fēng)險(xiǎn)，期望度量收益，在同時(shí)考慮資產(chǎn)風(fēng)險(xiǎn)和收益中尋找一種平衡。假設(shè)現(xiàn)有n種風(fēng)險(xiǎn)資產(chǎn)，rj表示第j（j=1，…，n）種風(fēng)險(xiǎn)資產(chǎn)的收益率，wj表示第j種風(fēng)險(xiǎn)資產(chǎn)的投資權(quán)重（其中n），則組合資產(chǎn)收益率為rp=w1r1+w2r2+…+wnrn。期望收益率、方差風(fēng)險(xiǎn)分別為：

式（1）～（2）中：投資權(quán)重向量 w=（w1，w2，…，wn）T；資產(chǎn)收益率向量 r=（r1，r2，…，rn）T；協(xié)方差矩陣 Q=（σij）n×n（其中 σij=cov（ri，rj））。

根據(jù)式（1）與式（2）可見(jiàn)，當(dāng)確定了投資權(quán)重向量w，組合資產(chǎn)的收益和風(fēng)險(xiǎn)也就確定了。記e=（1，1，…，1）T，參數(shù) r0為預(yù)設(shè)最小收益率，則M-V投資組合模型如下：

1.2下半方差—近似偏度投資組合模型

資產(chǎn)風(fēng)險(xiǎn)既包含了資產(chǎn)收益高于期望收益的風(fēng)險(xiǎn)，也包含了低于期望收益的風(fēng)險(xiǎn)。而投資者在實(shí)際投資時(shí)，更關(guān)心資產(chǎn)期望收益低于投資者預(yù)期收益水平的風(fēng)險(xiǎn)。這樣一來(lái)，提出了下半方差（lower semi-variance，SV）的概念。如果 SV（rj）=E［（min（rj-Erj，0）2］＜+∞，那么，第 j種風(fēng)險(xiǎn)資產(chǎn)的下半方差定義為：

假設(shè)除節(jié)假日外的n種風(fēng)險(xiǎn)資產(chǎn)，在一段連續(xù)時(shí)間內(nèi)，第 j（j=1，…，n）種資產(chǎn)在第 t（t=1，…，T）天的收益率為rtj，那么第j種風(fēng)險(xiǎn)資產(chǎn)的期望收益率矩估計(jì)為，方差、下半方差的矩估計(jì)分別為：

偏度衡量了資產(chǎn)收益率分布的不對(duì)稱(chēng)，當(dāng)偏度大于0時(shí)，意味著資產(chǎn)收益率大于期望的概率大一些，風(fēng)險(xiǎn)相對(duì)小一些。第j種風(fēng)險(xiǎn)資產(chǎn)的偏度Skew（rj）=E［rj-Erj］3，因正態(tài)分布的偏度為 0，方差和下半方差比值為2，考慮用方差和下半方差比值與2的差值近似偏度。那么根據(jù)式（4）與式（5）得到第j種風(fēng)險(xiǎn)資產(chǎn)的近似偏度矩估計(jì)為，由式（6）與式（7）得到 n種風(fēng)險(xiǎn)資產(chǎn)組合的近似偏度矩估計(jì)為：

以資產(chǎn)組合的下半方差為目標(biāo)函數(shù)，在M-V模型約束條件上引入偏度系數(shù)大于0，得到半方差—近似偏度模型（semi-variance approximate skewness model，SVASM）。那么，SVASM模型可以表示為：

1.3負(fù)半熵—下半方差—近似偏度投資組合模型

風(fēng)險(xiǎn)本質(zhì)上是資產(chǎn)收益率的不確定性。信息熵是系統(tǒng)的無(wú)序程度與信息量的有效結(jié)合，信息熵?cái)?shù)值越小，樣本不確定性程度就越小。相比只能反映分布二階矩特征的方差，信息熵能更加準(zhǔn)確度量組合資產(chǎn)的全部風(fēng)險(xiǎn)。假設(shè)X是離散型隨機(jī)變量，其概率分布律為 pi=P（X=xi），pi≥0，i=1，…，n，那么，信息熵為如果X是連續(xù)型隨機(jī)變量，M.Rao［15］給出了一種新的信息度量方法——累積剩余熵，其表達(dá)式為：

對(duì)于投資者而言，更加在乎組合資產(chǎn)收益低于期望收益的信息。這樣一來(lái)，根據(jù)式（9）提出負(fù)半熵（negative half entropy，簡(jiǎn)稱(chēng) NE）的概念。負(fù)半熵公式為：

負(fù)半熵本質(zhì)是一種期望，它衡量了組合資產(chǎn)收益低于期望收益的信息。基于頻率代替概率的思想，可以獲得組合資產(chǎn)負(fù)半熵的矩估計(jì)，步驟如下：

步驟1 將第j種風(fēng)險(xiǎn)資產(chǎn)在第t天的收益率rtj減去樣本均值 ˉrj，獲得新序列 ytj=rtj-ˉrj；

步驟2 將新序列ytj分成長(zhǎng)度相等的m個(gè)子區(qū)間，記載每個(gè)子區(qū)間中新序列ytj小于0的頻數(shù)Nij（i=1，…，m，j=1，…，n）；

步驟3 用頻率估計(jì)概率的方法，獲得收益率序列 ytj落在第 i（i=1，…，m）個(gè)區(qū)間上的概率

步驟5 權(quán)重向量為 w=（w1，…，wn）的組合資產(chǎn)收益的負(fù)半熵為

下半方差常常受資產(chǎn)變量分布的影響，因而用負(fù)半熵補(bǔ)償下半方差度量組合資產(chǎn)收益低于期望收益的那部分風(fēng)險(xiǎn)，這樣一來(lái)，在SVASM模型基礎(chǔ)上，構(gòu)建負(fù)半熵 —下半方差 —近似偏度模型（negative half entropy lower semi-variance approximate skewness portfolio model，NESVASM）為：

其中 λ為調(diào)節(jié)參數(shù)［16］，需滿(mǎn)足 λ＞0；H^-（w）表示n種風(fēng)險(xiǎn)資產(chǎn)組合的負(fù)半熵。

2 實(shí)證分析

2.1 數(shù)據(jù)的選取與處理

在實(shí)際投資組合中投資資本有限，投資者在考慮選取資產(chǎn)時(shí)，既要兼顧分散風(fēng)險(xiǎn)又要考慮自身資本承受能力，因此投資組合中的資產(chǎn)數(shù)量不宜過(guò)多。根據(jù)投資組合原理以及對(duì)中國(guó)金融市場(chǎng)調(diào)查研究得出的經(jīng)驗(yàn)法則，當(dāng)投資組合中證券數(shù)量過(guò)多時(shí)，組合對(duì)非系統(tǒng)風(fēng)險(xiǎn)的分散作用開(kāi)始減弱。因此，在組合投資時(shí)選擇13種風(fēng)險(xiǎn)資產(chǎn)，此時(shí)對(duì)非系統(tǒng)風(fēng)險(xiǎn)的分散作用較大。從瀘深300中，涉及銀行、通信、建筑等多個(gè)行業(yè)選擇相對(duì)平穩(wěn)的13只股票進(jìn)行研究，所選股票見(jiàn)表1。為保證模型的時(shí)效性，選取2016年3月1日至2017年3月1日，除節(jié)假日外的日收盤(pán)價(jià)進(jìn)行實(shí)證分析。假設(shè)第j只股票在第t天的收盤(pán)價(jià)為stj，則收益率為rtj=ln stj-ln s（t-1）j，t=1，…，T，j=1，…，n。

2.2 描述性分析

根據(jù)定義，計(jì)算出各只股票的樣本均值與方差、下半方差與負(fù)半熵、樣本偏度與近似偏度，如表2所示。

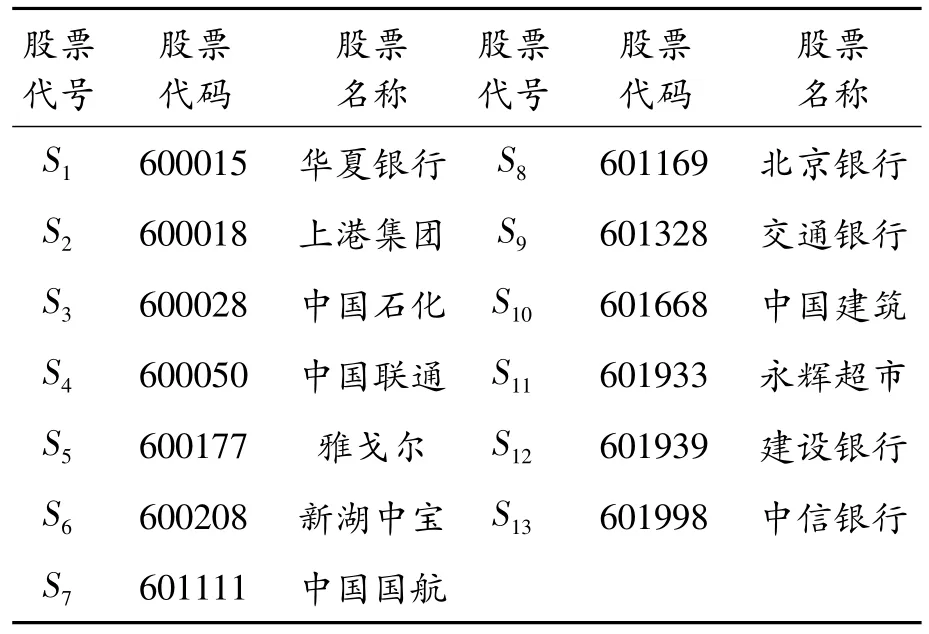
表1 選取的13只股票

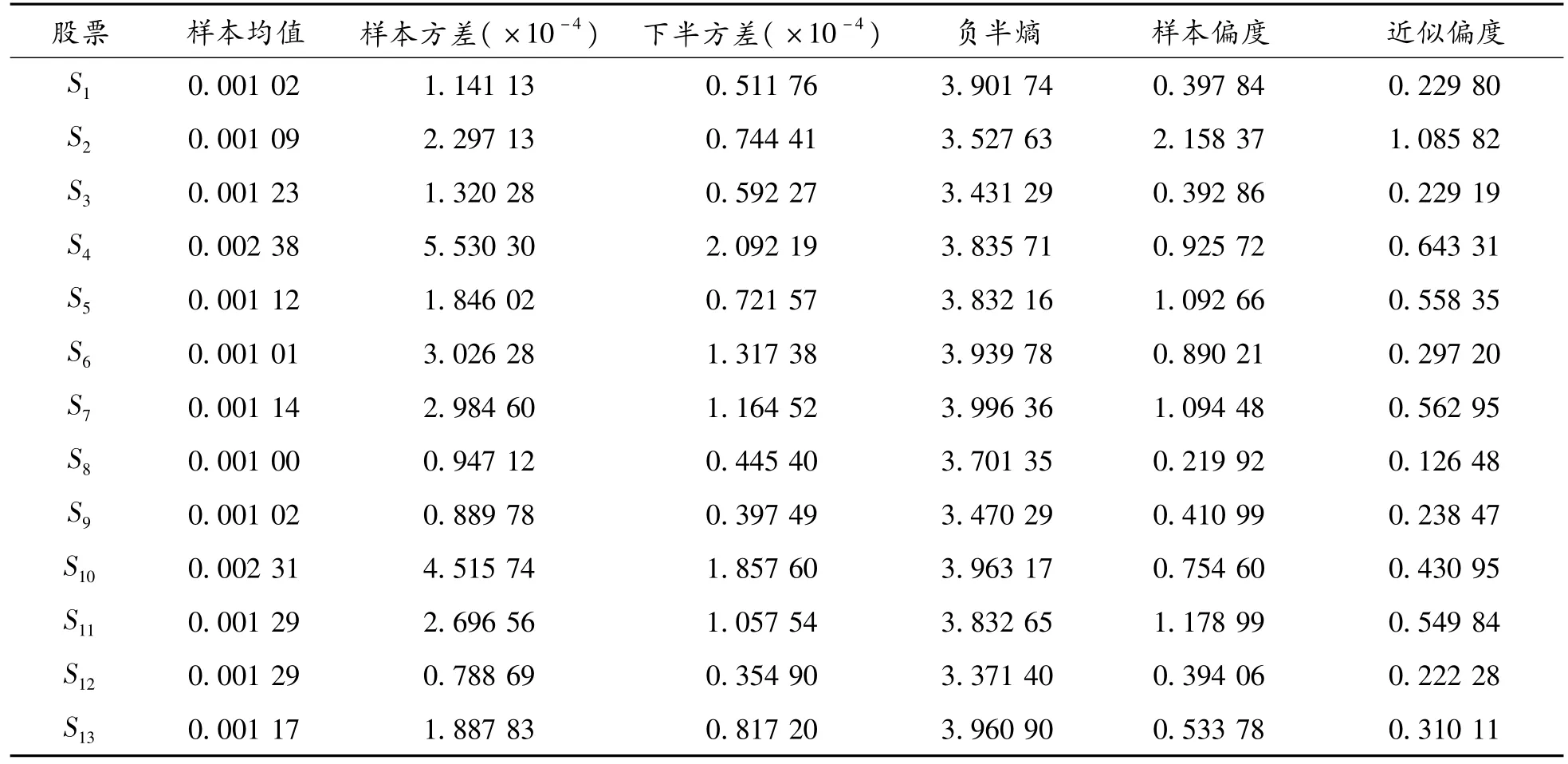
表2 各只股票的樣本均值與方差、下半方差與負(fù)半熵、樣本偏度與近似偏度

從表2可以看出：①在13只股票中，股票S2、S4的下半方差比其方差要小得多，可見(jiàn)下半方差在方差中并非對(duì)稱(chēng)的，用下半方差度量風(fēng)險(xiǎn)能更加準(zhǔn)確地度量股票收益向下波動(dòng)的那部分風(fēng)險(xiǎn)；②負(fù)半熵與下半方差進(jìn)行比較，13只股票的負(fù)半熵與下半方差有大致相同的增減趨勢(shì)，這與負(fù)半熵和下半方差都是度量低于期望收益風(fēng)險(xiǎn)相吻合；③近似偏度與樣本偏度進(jìn)行比較，股票S2和S8是樣本偏度值中最大和最小的2只股票，在近似偏度值中股票S2和S8同樣是最大和最小的2只股票，并且近似偏度與樣本偏度有幾乎一樣的大小趨勢(shì)，這表明近似偏度與真實(shí)偏度存在較好的擬合效果。

2.3 模型NESVASM的求解

根據(jù)拉格朗日乘子法和梯度下降法對(duì)模型進(jìn)行編程求解，模型NESVASM中存在調(diào)節(jié)參數(shù)λ和收益參數(shù)r0，圖1給出了模型在相同收益參數(shù)、不同調(diào)節(jié)參數(shù)下，13只股票的投資組合情況。

從圖1可以看出：①模型求解的投資權(quán)重wj分布在第 2、3、8、9、11、12只股票，沒(méi)有呈現(xiàn)集中分布現(xiàn)象，符合分散投資理念；②隨著調(diào)節(jié)參數(shù)λ的逐漸增大，負(fù)半熵的作用逐漸顯現(xiàn)，負(fù)半熵更小的股票S9和S12投資權(quán)重呈增加的趨勢(shì)，負(fù)半熵更大的股票S8和S11的投資權(quán)重呈減小的趨勢(shì)，這也表明用負(fù)半熵來(lái)衡量風(fēng)險(xiǎn)時(shí)，股票S8和S11被度量出了更多的風(fēng)險(xiǎn)，模型更看好股票S9和S12。

圖2給出了模型在相同調(diào)節(jié)參數(shù)、不同收益參數(shù)下，13只股票的投資組合情況。

從圖2可以看出：①隨著收益參數(shù)r0的逐漸增大，呈現(xiàn)股票 S4、S10替代股票 S2、S3、S8、S11的現(xiàn)象，可見(jiàn)股票S4和S10發(fā)生超額收益的可能性更大；②調(diào)節(jié)參數(shù)也可看作投資者對(duì)負(fù)半熵的偏好程度，不同投資者對(duì)風(fēng)險(xiǎn)偏好和收益要求不同，調(diào)節(jié)參數(shù)和收益參數(shù)可根據(jù)實(shí)際情況進(jìn)行適當(dāng)調(diào)整。

表3給出了在不同調(diào)節(jié)參數(shù)λ和收益參數(shù)r0下NESVASM模型的收益率、下半方差、負(fù)半熵、近似偏度值。

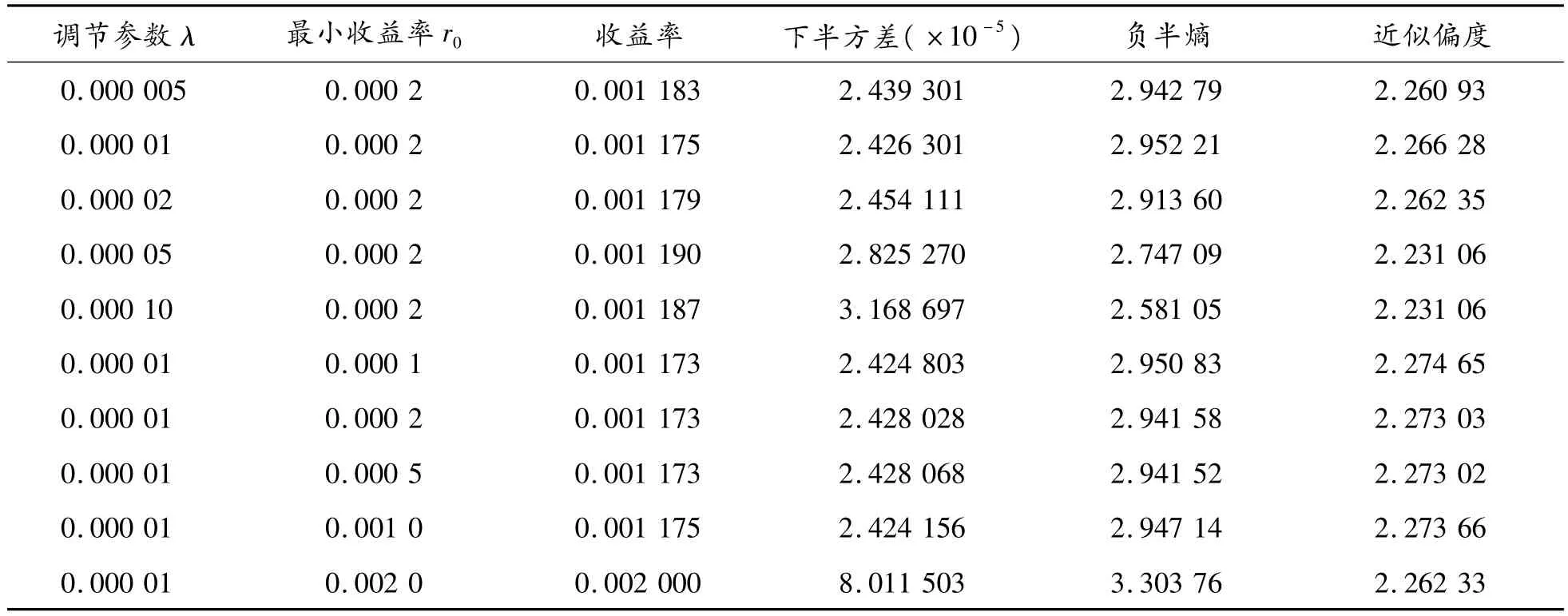
表3 NESVASM模型在不同調(diào)節(jié)參數(shù)λ和收益參數(shù)r0下的結(jié)果

從表3可以看出：① 在固定收益參數(shù)r0時(shí)，隨著調(diào)節(jié)參數(shù)λ的逐漸增大，下半方差呈增長(zhǎng)趨勢(shì)，負(fù)半熵呈減小趨勢(shì)，這與負(fù)半熵在目標(biāo)函數(shù)中比例變大相吻合；② 同樣，在相同收益參數(shù)r0條件下，NESVASM模型在λ=0.000 01時(shí)，負(fù)半熵比在λ=0.000 005時(shí)的負(fù)半熵更大，表明此時(shí)負(fù)半熵度量出了更多的高階矩風(fēng)險(xiǎn)，使得本應(yīng)更小的負(fù)半熵出現(xiàn)變大的現(xiàn)象；③ 在固定調(diào)節(jié)參數(shù)λ條件下，隨著收益參數(shù)r0的增大，下半方差和負(fù)半熵呈增大的趨勢(shì)，這與收益更大風(fēng)險(xiǎn)更大相吻合。

2.4 模型NESVASM與MV模型、SVASM模型的比較

為進(jìn)一步說(shuō)明負(fù)半熵對(duì)投資組合的影響，取定模型NESVASM中參數(shù)λ=0.000 01，r0=0.000 2，與M-V、SVASM模型的投資權(quán)重進(jìn)行比較，結(jié)果見(jiàn)表4。

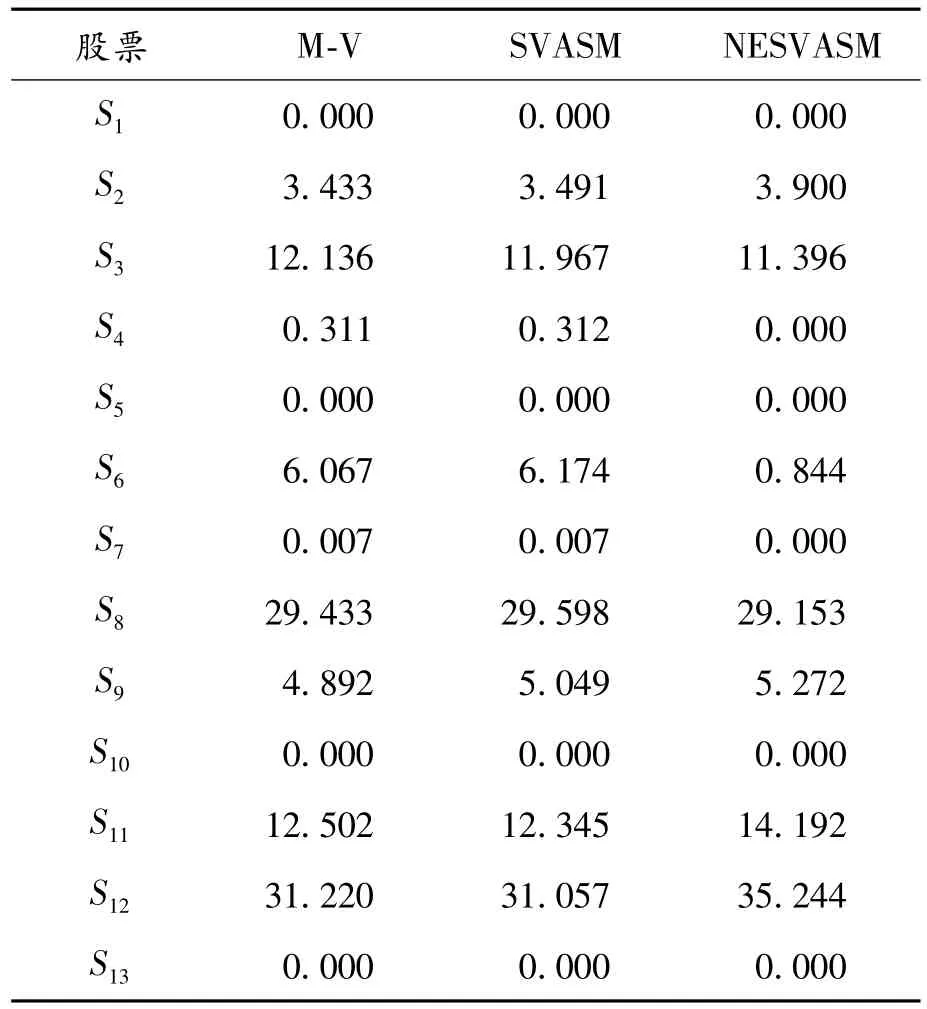
表4 在3種不同模型下的權(quán)重情況 %

從表4可以看出：① 與SVASM模型比較，NESVASM模型中股票S3、S6、S8的權(quán)重比例有所減小，股票 S2、S9、S11、S12的權(quán)重比例有所增加，這可能是負(fù)半熵度量出了股票S3、S6、S8的下半方差風(fēng)險(xiǎn)外其他高階矩風(fēng)險(xiǎn)所導(dǎo)致的結(jié)果；②特別是在股票S6、S11、S12上的權(quán)重比例存在明顯的變化，為投資者進(jìn)行選股時(shí)給予更多理性參考。

通過(guò)計(jì)算得到3種模型下的收益率、下半方差、負(fù)半熵、近似偏度，結(jié)果見(jiàn)表5。

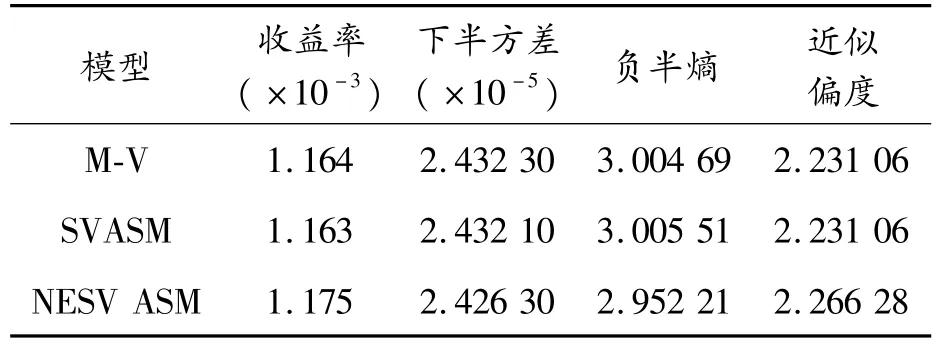
表5 M-V、SVASM、NESVASM模型的結(jié)果

從表5可以看出：與M-V、SVASM模型相比，模型NESVASM收益更大，風(fēng)險(xiǎn)度量指標(biāo)中下半方差和負(fù)半熵均更小，并且組合資產(chǎn)偏度也存在明顯提升。可見(jiàn)，結(jié)合負(fù)半熵的NESVASM模型更能反映組合資產(chǎn)所面臨的風(fēng)險(xiǎn)，能更有效地規(guī)避風(fēng)險(xiǎn)，為投資者在配置資產(chǎn)時(shí)提供更加合理的選擇。

3 結(jié)論

在傳統(tǒng)M-V模型的基礎(chǔ)上，考慮到投資者更關(guān)心資產(chǎn)收益能否達(dá)到預(yù)期收益的心理，通過(guò)用負(fù)半熵補(bǔ)償下半方差衡量資產(chǎn)收益低于預(yù)期收益的風(fēng)險(xiǎn)，并在約束條件中引入偏度系數(shù)，構(gòu)建NESVASM模型。通過(guò)選取13只股票進(jìn)行實(shí)證分析，發(fā)現(xiàn)NESVASM模型能獲得更大的收益，能更好地規(guī)避風(fēng)險(xiǎn)，并且發(fā)生超額收益的可能性更大。在理論上，結(jié)合負(fù)半熵與半方差度量風(fēng)險(xiǎn)的NESVASM模型，規(guī)避了它們單獨(dú)度量風(fēng)險(xiǎn)存在的缺陷；在實(shí)際投資時(shí)，NESVASM模型從方差和信息熵的角度度量資產(chǎn)收益低于預(yù)期收益風(fēng)險(xiǎn)，給風(fēng)險(xiǎn)厭惡型投資者更多的理性指導(dǎo)，在股票選擇和風(fēng)險(xiǎn)預(yù)測(cè)方面也具有指導(dǎo)意義。此外，模型約束條件也可考慮引入正半熵大于負(fù)半熵，本文中實(shí)證分析也可考慮期貨、期權(quán)、債權(quán)等衍生產(chǎn)品或流動(dòng)性因素，使模型更加切合真實(shí)的金融市場(chǎng)。