圍繞課程目標設計課堂教學

李雙雙

【關鍵詞】課程目標;學科核心素養;教學案例;高中數學

《普通高中數學課程標準（2017年版）》（以下簡稱“新課標”）提出了培養學生的學科核心素養等課程目標。那么，如何理解課程目標并在課堂教學中實現它們呢？為此，筆者請教了專家也研讀了新課標相關解讀文獻，現結合蘇教版高中數學必修4第1章“三角函數”起始課的教學實踐，談談自己的一些思考。

一、對課程目標的理解

新課標對于課程目標，從數學基礎知識、基本技能、基本思想、基本活動經驗（簡稱“ 四基”），數學角度發現和提出問題的能力、分析和解決問題的能力（簡稱“四能”），數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析（簡稱“六大核心素養”），會用數學眼光觀察世界、數學思維思考世界、數學語言表達世界（簡稱“三會”）等不同的角度加以論述。新課標指出：“‘四基是培養學生數學學科核心素養的沃土，是發展學生數學學科核心素養的有效載體。教學中要引導學生理解基礎知識，掌握基本技能，感悟數學基本思想，積累數學基本活動經驗，促進學生數學學科核心素養的不斷提升。”[1] 因此，筆者以為它們之間的邏輯關系為“四基”是基礎，數學學科核心素養是靈魂，“四能”是抓手，“三會”是終極性目標。

1“. 四基”——課堂教學的基礎目標。

對于“四基”，在每一節課具體內容的教學中，教師一般都會思考有無夯實基礎知識、基本技能和基本思想。但是，對于“基本活動經驗”，很多教師尚未足夠重視，還需要我們在教學中充分創設問題情景，引導學生“基于原有的數學活動經驗”去“再發現”地學習數學，從而在學習的過程中不斷豐富學生的數學活動經驗。

2.數學學科核心素養——數學教學的長期目標。

數學學科核心素養（以下簡稱“核心素養”）是數學課程目標的集中體現，是“四基”的繼承和發展。核心素養的形成不是一蹴而就的，是在數學學習過程中逐步形成的。“四基”（尤其是基礎知識）緊密貼合相關的數學知識，因此就具有顯性的特征;而數學核心素養的形成隱含于數學知識的學習過程中，也就具有隱性的特征。這就需要教師根據教學內容，挖掘與教學內容相關聯的核心素養目標，并且以恰當的問題與情景為載體，培養學生的核心素養。在教學中，應當把核心素養作為一個長期的目標，融入每一節課的教學中。因此在課堂教學時，我們可以確定兩條目標主線：“明線”是“四基”;“暗線”是核心素養。

3“四能”——數學素養提升的抓手。

“四能”的核心是“問題”。課堂教學中，應當以“四能”為抓手，培養學生的問題意識。讓學生發現并提出問題、分析并解決問題，激發學生的好奇心;讓學生在數學活動中，理解數學的概念、掌握數學技能、形成數學思想方法、積累數學活動經驗，經歷邏輯推理、數學建模、直觀想象、數學運算、數據處理等過程，從而有利于“四基”和核心素養的形成。

當然，提高“四能”和“四基”與提升核心素養是相互促進的，學生一旦具備了良好“四基”和核心素養，就能夠基于已有的解決問題的活動經驗，經歷數學抽象、邏輯推理和數學建模等思維過程，發現并提出問題、分析并解決問題。

4“三會”——數學教育的終極目標。

“三會”非一朝一夕能夠形成的，它是數學教育的終極性目標。因此，“三會”這一目標并不需要我們在每一節課上去刻意地關注和落實。只要我們在平時的教學中，堅持以學生發展為本，發揮學生的主體地位，關注“四能”、夯實“四基”、發展核心素養，就能夠使學生逐步學會“三會”。

二、以課程目標為導向的教學實踐

基于上述理解，筆者執教了蘇教版高中數學必修4第1章“三角函數”第1課時，教學內容包括“章引言”和“任意角”兩個部分。主要教學環節與設計意圖如下。

1.教學目標的制訂。

根據教學內容和課程目標，確定了本節課的教學目標：

（1）初步了解周期現象和本章的主要研究內容;了解任意角、正角、負角、零角、象限角的概念，掌握與給定角α終邊相同的角的表示方法。

（2）通過改變摩天輪的旋轉方向、旋轉時間等變量，讓學生發現問題，感受學習任意角的必要性，并借助已有的數學活動經驗解決問題，建構任意角、正角、負角、零角、象限角的概念，豐富學生的數學活動經驗，發展學生數學抽象、邏輯推理和數學建模等核心素養。

【設計意圖】首先，關注“四基”。這里不僅關注到相關的基礎知識、基本技能和基本思想，更重要的是讓學生感受到學習新知識（任意角）的必要性，并借助于已有的活動經驗，自我建構新的概念，讓學生獲得更多的數學活動經驗。其次，根據本節課內容的特點，確立了培養學生數學抽象、邏輯推理、數學建模等核心素養的目標。最后，以“四能”為抓手，通過控制摩天輪的旋轉方向、旋轉時間等變量，讓學生發現問題：初中所學的角“不夠用”了，需要進一步分析問題、提出解決方案。

2.章引言課的教學

章引言課的教學，能夠幫助學生厘清知識的來龍去脈、縱橫聯系和可能應用，形成全章知識概覽和認知思路框架。

筆者由摩天輪引入“周期現象”，經過數學抽象，設計了如下問題，進而開啟對任意角的研究。

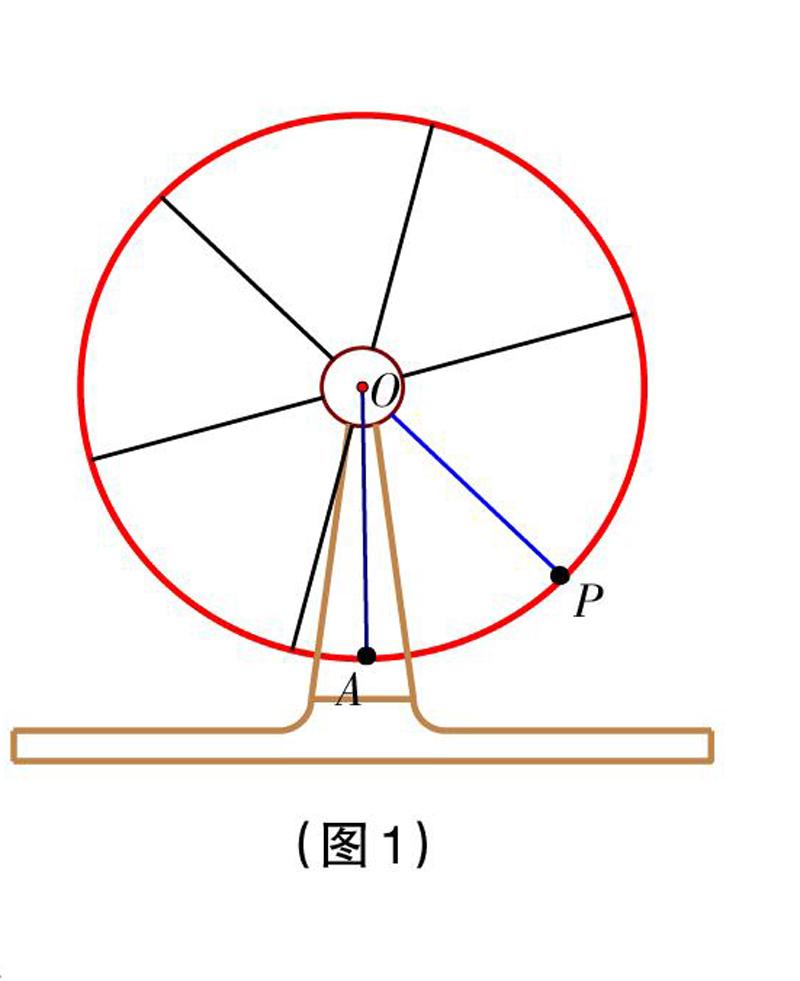
問題1：如圖1所示，已知某摩天輪的直徑為100m，按逆時針方向勻速旋轉，6分鐘轉過1 周。若小明從點A 處乘坐摩天輪，旋轉1分鐘時小明所在的位置記為點P，請你用恰當的方法來表示點P的位置（相對于點A）。

【設計意圖】（1）通過章引言課的教學，讓學生從整體把握數學內容，幫助學生厘清“三角函數”這一章的內容與邏輯關系，整體把握本章的教學內容：幫助學生發現并初步領會“周期現象”這一數學規律;通過研究圓O 上點P 位置的三種不同表達方法——P（r，α），P（r，l）和P（x，y），為本章將要繼續學習的內容做好鋪墊。

（2）著力培養學生的數學學科核心素養。首先，通過摩天輪這一實例，讓學生經歷數學抽象的過程，發現“摩天輪旋轉”這一實例背后所蘊含的周期現象;其次，通過對平面內圓O 上點P 位置的3種不同表示方法的研究，在培養學生核心素養的同時，讓學生全面而深刻地理解數學，能夠運用不同的方法表達具體的問題。

（3）通過“摩天輪旋轉”這一實例引入三角函數的學習，能夠讓學生體會到數學來源于生活，并為今后運用三角函數知識來解決與“摩天輪旋轉”相類似的應用題埋下伏筆。

3.任意角概念的教學。

筆者在上面問題1的基礎上，繼續追問。

追問1：經過多長時間后，小明還會再一次回到點P 位置？小明第2次到達點P 時，一共轉過了多少角度？第3次呢？

追問2：若摩天輪按順時針方向旋轉（其他條件不變），旋轉1分鐘時小明所在位置記為點Q，從點A 到點Q，轉過的角度是多少？第2次、第3次到達點Q位置時一共轉過了多少角度呢？

問題2：從剛才的摩天輪旋轉的實例中，我們發現過去所學的角已經“不夠用”了，于是我們需要將角的范圍加以擴大，如何來擴大角的范圍呢？

【設計意圖】（1）讓學生明白為什么要學習“任意角”。由追問1讓學生發現初中所學習的0°～360°的角已經“不夠用”了，認識到將角的范圍進行擴充的必要性;再由追問2讓學生產生認知沖突，并依據已有的數學活動經驗，用正角、負角表示按照不同方向旋轉所形成的角。（2）通過改變摩天輪的旋轉方向、旋轉時間等變量，讓學生發現并提出問題，并經過自己的思考，初步給出解決問題的方案。在這一學習過程中，培養學生數學抽象與類比推理等素養，調動學生學習數學的積極性。進一步豐富學生的數學活動經驗。

4.終邊相同角的教學。

（1）建立恰當的坐標系表示角。

問題3：本章我們將要研究三角函數，根據

我們前面研究函數的經驗，我們需要在坐標平面內研究角。你打算如何建立適當的坐標系來研究角呢？有什么好處？

（2）探究終邊相同角之間關系。

問題4：角-300°，-150°，-60°，60°，210°，300°，420°分別是哪個象限角？其中哪些角的終邊相同？

追問1：從問題4，你發現終邊相同的角彼此之間有什么關系？你能寫出與60°角終邊相同的角的集合嗎？

追問2：與角α 終邊相同的角的集合是什么呢？

【設計意圖】（1）問題3讓學生思考“如何建立坐標系來研究角”，在這一過程中，有利于培養學生分析問題、解決問題的能力，促進學生邏輯推理能力的提高和數學建模意識的形成。（2）問題4 及追問1 和2，體現了“從特殊到一般”的數學思維過程，符合學生的認知特點，讓學生在得到與角α 終邊相同的角的集合的表達形式的同時，理解數學的思維方法。（3）在得到了“與角α 終邊相同的角的集合為{β|β=α+k·360°，k∈Z}”后，提出問題“代數表達式α+k·360°（k∈Z）表示的意義是什么？這里反映了一個什么現象？”讓學生學會從“數”與“形”兩個角度思考問題，領會這一表達式中所蘊含的“周期現象”，加深對周期現象的理解。

三、教學反思

以上介紹了筆者自己學習運用課程目標的體會和教學案例。對于這一節課，如果我們不去深入挖掘教材內容背后所蘊含的學科核心素養，僅僅關注知識目標，那么對學生學科核心素養的形成是極為不利的，長此以往，課程標準提出的課程目標也就難以得到全面落實。因此，在教學中，要大力培養學生的問題意識，讓學生思考“為什么學（研究價值）、學什么（研究內容）、如何學（研究方法）”，以期實現這一輪課程改革提出的課程目標。