基于變易理論指導下的大學數學概念教學設計

劉生貴

[摘 要]數學概念是建構數學理論大廈的基石，是學生進行數學思維的核心和基礎。學生在解決計算、證明、作圖等具體數學問題中無時無刻不用到數學概念。在課堂教學中，以“變易理論”為教學設計的理論指導，對于那些對學生難于理解的大學數學概念，運用變易圖式設計教學，可以有效達到對數學概念關鍵屬性的辨析，幫助學生掌握學習內容，提高教學質量。

[關鍵詞]變易理論;概念教學;大學數學

[中圖分類號] G642 [文獻標識碼] A [文章編號] 2095-3437（2020）12-0108-03

一、變易理論簡介

變易理論理論的研究始于是世界著名教學專家、瑞典哥德堡大學的馬飛龍（Ference Marton）教授所提出的現象圖式學[1]。現象圖式學認為，學習一定有其內容， 而每一個體對學習內容的認識都有其個別的獨特視野。在這些視野中，有一些能夠體現事物本質的關鍵屬性，高明的看法能夠辯識這些關鍵特征：而所謂學習困難就是學習者難以辨識這些關鍵特征[2]。

變易理論認為我們不能在不變狀態中去感知事物的存在價值和性質。沒有某方面的變動，事物特性只會是潛在隱藏，這對于認識事物的存在意義并沒有幫助[3]。近些年，變易理論得到廣泛的傳播和研究，在全球享有很高的聲譽。目前，已有眾多教育工作者將變易理論作為設計教學的指導工具，進行教學的研究和改革，取得了豐碩的成果。但這些研究大多是針對中小學的教學，目前對于大學的教學方面的研究甚少[4-7]。筆者在實際教學中研究發現，變易理論同樣可以應用于大學數學的教學設計，并取得很好的教學效果。

數學概念是建構數學理論大廈的基石，是學生進行數學思維的核心和基礎。學生在處理計算、證明、作圖等具體數學問題中無時無刻不用到數學概念。學習概念性知識有助于發展更高層次的數學思維以解決數學問題。數學概念是比較抽象的，學生學習數學的思考過程大多是把抽象的概念與生活經驗相聯系，用他們的生活經驗去解讀抽象的數學概念。為讓學生獲得清晰的數學概念，教學時應把抽象的數學概念具體化呈現，讓學生經驗變易圖式及反思學習數學概念。所以說，數學概念的學習是基于變易的。

在大學數學課堂教學中，很多老師都會覺得，只要把問題講得很詳細、很清楚，學生便會得到跟老師一樣的理解。然而事實上的結果常常與假設相差甚遠，這讓老師們感到非常困惑。老師們常常會把這些歸因于學生的學習動機或數學基礎、天賦能力。

下面是筆者在給工科學生上高數的不定積分的概念時，遇到的一個小插曲。

定義：定義在區間I上，[f（x）]的帶有任意常數項的原函數，稱為[f（x）]在區間I上的不定積分，記作[ f（x）dx]。即，如果[F（x）]為I的一個原函數，則

其中記號[ ]稱為積分號，[f（x）]稱為被積函數， [f（x）dx]稱為被積表達式，[x]稱為積分變量。

筆者還是按常規的方法進行這個概念的教學，但在講完后續課程分部積分后的一次學生交流，讓我意識到了教學中的問題。學生問我：“老師，我按下面這樣做，結果對不對？”

最初一看到這個問題我感覺很不可思議，但我還是耐下性子問學生為什么會這樣想呢？學生回答說：“因為[（tanx）=sec2x。]”我的天，學生竟然是這樣想的！

“變易理論”認為，老師之所以難于明白學生學習的真正困難所在，不了解學生如何思考的和如何學習的，主要原因在于忽略了教學內容的某些關鍵特征，而這些經常“視而不見”關鍵特征卻是教師習以為常以至于不會特別去處理的東西，這些處于老師盲點的關鍵特征恰恰便是造成學生學習困難的主要原因[8]。

二、基于變易理論指導下大學數學概念的教學設計

變易理論認為，要認識某個事物，就必須注意到這個事物與其他事物之間的不同之處。為了注意這個事物與其他事物在某個屬性上的不同，這個屬性就必須在某個維度上發生變化。在所有其他屬性都保持不變的情況下，這個差異才可以被識別出來[3]。將這一理論應用于課堂教學實踐，通過設計適合學生學習的變易圖式進行教學，幫助學習掌握學習內容的關鍵特征，對于提升學生學習素質，尊重學習過程中的個體差異具有非常重要的意義。

變易理論應用于課堂教學，主要體現為對學科教學內容的處理，而不是教學活動形式的選擇與組織[9]。在運用變異理論設計教學過程中，教師首先必須清楚學生應區分哪些關鍵屬性，能辨出是哪些特征有可能導致學生在學習過程中出現困難。但很多時候，教師跟學生一樣，還未能對教材有足夠的認識，也未能區分出這些關鍵特征，或者某些關鍵屬性對于教師來說并不困難，或由于太習以為常而把它忽略。只有診斷學習困難并確認學習內容的關鍵屬性，才能為教學設計提供有效的依據。常見的方法是對學生進行訪談，以了解學生的想法，或設計一個前測問卷調查，借以診斷該群學生的學習難點[10]。只有對學生的學習困難所在以及教學內容的關鍵屬性有深入的了解，運用變易圖式進行教學設計才具有針對性。

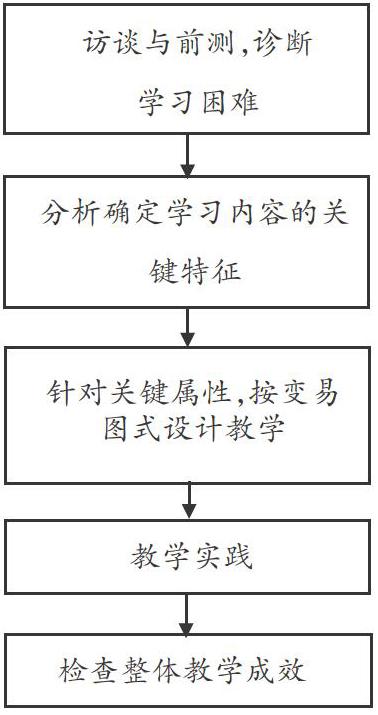
運用變易理論設計教學的一般過程如右圖。下面分別以函數的連續性和不定積分的概念為例，簡要介紹一下變易理論在數學概念教學設計上的應用。

（一）連續函數概念的變易教學設計

函數是高等數學的主要研究對象，而極限作為其主要的研究方法，連續性則作為研究函數的橋梁，由此可見連續性概念對高數學習的重要性。很多時候，老師雖然自認為把這個概念講得非常清楚了，但從課后訪談和作業情況來看，仍有很多這個學生對理解并不透徹，掌握不好。

定義 設函數[y=f（x）]在點[x0]的某個領域有定義，如果函數[f（x）]當[x→x0]的極限存在，且

則稱函數[y=f（x）]在點[x0]處連續。

在進行研究前期，為了更好地了解學生狀況，筆者所帶的課題組對該問題進行了前測與訪談。測試對象主要是已學過該內容的大一與大二學生，其中既有數學專業學生，也包含非數學專業的學生。前測問卷如下：

A. 完全理解這個概念，能結合實際判斷函數的連續性;

B. 有些理解，但不透徹，對一些復雜些的函數難于判斷函數的連續性;

C. 似懂非懂，不大明白函數連續應具備的三個條件;

D. 完全不理解這個概念。

課題組共收回有效問卷123份（人次），其中數學專業99份（人次），非數學專業24份（人次）;這123人中有大一的學生55人，有大二的學生68人。收回的問卷情況如下。

由上表可知，雖然學生已經學習過函數連續的概念，但僅有13.8%的對這個概念有比較透徹的理解，而似懂非懂或理解比較模糊占比超過了百分之八十，這個結果大大出乎老師的意外。

通過對教學內容的分析與討論，結合與學生訪談情況，研究小組確定連續函數的關鍵特征如下。

關鍵特征1：函數在點[x0]的某個領域有定義。

關鍵特征2：函數[f（x）]當[x→x0]的極限存在。

關鍵特征3：函數[f（x）]的極限[limx→x0f（x）]必須等于[f（x0）]。

為讓學生更好地突出和辨析這些關鍵特征，依次設計如下變易圖式。

變易圖式1：

變式例題1 考察下列函數在[x=0]處的連續性。

變易圖式2：

變式例題2 考察下列函數在[x=0]處的連續性。

變易圖式3：

[變 不變 審辨的關鍵屬性 函數在某點的值 函數的部分表達式 函數在某點連續，在該點的極限必須與該點的函數值相等. ]

在用變易圖式對兩個實驗班完成教學后，對該部分學生進行了后測，問卷如前。課題組共收回有效問卷98份（人次），結果如下。

由后測結果可以看到，選擇A（理解這個概念，能結合實際判斷函數的連續性）的人數所占百分比大幅提升至79.7%; 而問卷回答選B、C、D，即不能很好理解這個概念的人數所占百分比大幅下降至21.3%。可見，運用變式（變易）教學效果顯著。

（二）不定積分概念變易的教學設計

[被積函數][積分變量]

這是個非常重要也非常基礎的概念，如果這個概念理解不透徹，不僅會導致后繼的換元積分法和分部積分法產生學習困難，還將影響整個大學數學的學習。這個概念表面看起來并不難懂，多數老師在講這個概念時都會熟視無睹輕易帶過，認為學生也能很容易弄懂，但事實上并非如此。學生在學習積分法時感覺很難，很大原因就是對不定積分概念的理解并不透徹，關鍵屬性被忽略，前面筆者所介紹的教學交流小插曲正印證了這一點。

據與學生訪談與分析，研究小組認為不定積分的關鍵屬性有下面兩個：

關鍵屬性1：積分函數。

關鍵特征2：積分變量。

在設計教學時，為讓學生更好辨析關鍵屬性，依次作如下變易圖式。

變易圖式1：

變式例題4 求下列函數的不定積分。

為了幫助學生克服忽視積分變量，更好地辨析關鍵屬性2，為后面換元積分掃清障礙，設計了如下變易圖式2：

變式例題5 求下列函數的不定積分。

由例5，學生會發現，被積函數一樣，當積分變元變化時，求得的原函數是不一樣的，學生對不定積分的定義會有新的認識，為后繼課程的學習打下良好的基礎。

三、結語

學習離不開對事物差異的感知。沒有事物屬性的差異變化，則學習者很難獲得對事物屬性真正全面且深刻的理解。變化事物不同的屬性組合，可以有意突出事物中處于學習者“盲點”的某些屬性，并與其他屬性區分開，引導學習者關注同一事物的各方面的特點，從而學會從不同的角度來認識同一事物。

有別于其他教學理論，變易理論應用于課堂教學，主要體現為針對學科教學內容的加工，而不是教學方法的選擇或教學的組織。以“變易理論”為理論指導，在教學中通過設計變易圖式來幫助學生克服困難掌握學習內容，可以有效改善我們的教與學。盧敏玲教授和孫旭花教授在實證研究中發現，運用變易理論指導教學可以簡單概括為：找出教與學之間的關系，抓重點，找難點，用變易圖式突顯學習內容的關鍵特征，是行之有效的教學手段[11]。

[ 參 考 文 獻 ]

[1] Maton F. Sameness and Difference in Transfer[J]. The Journal of The Learning Science，2006，15（4）：499-535.

[2] 梁玉麟，勞傅燕華，江巧妍. 數學課堂學習研究實踐與數學基本概念的教學[M].合肥：安徽教育出版社，2011.

[3] 郭永賢.課堂學習研究概論[M].合肥：安徽教育出版社，2011.

[4] 陳紅兵. 創設有效的學習空間：變異理論視野下的課堂教學[J]. 教育學報，2013（5）：52-60.

[5] 高寶玉，盧敏玲，龐永欣，等. 課程決定的實踐歷程：課堂學習的個案研究[J]. 當代教育科學，2009（18）：4-9.

[6] 從立新.步步為營：運用變異理論指導教學操作步驟[J]. 教育學報，2013，9（5）：68-74.

[7] 陳建翔. “變易理論”對傳統遷移觀的超越及啟發[J]. 中國教育學刊，2009（1）：30-33.

[8] 盧敏玲.變易理論和優化課堂教學[M].合肥：安徽教育出版社，2011.

[9] 易進. 課堂要為學生學習創造條件：變異理論運用于教學實踐的探索與思考[J]. 課程·教材·教法，2014，34（6）：104-109.

[10] 李樹英，高寶玉.課堂學習研究實踐手冊[M].合肥：安徽教育出版社，2011.

[11] 盧敏玲，孫旭花. 教如何有助于學：一個概念的教與學關系之實證研究：香港課堂學習研究課的啟示[J].當代教育科學，2011（10）：25-29.

[責任編輯：林志恒]