算理貫通 理法相融

靳培英 徐小群 尚林 鞏子坤

【摘? ?要】要實現(xiàn)算理貫通，就要促進多種表征貫通;要實現(xiàn)理法相融，就要促進算理走向算法。教師采用行動研究法，探查了有利于算理貫通、理法相融的兩位數(shù)加一位數(shù)（不進位）、整十數(shù)的學習路徑。該加法的關鍵與本質是“相同計數(shù)單位上的數(shù)才能夠直接相加”，這為加法豎式的“相同數(shù)位對齊”做好了鋪墊。優(yōu)化的學習路徑由4個層次推進的認知任務構成：整十數(shù)加一位數(shù)、整十數(shù)加整十數(shù)→兩位數(shù)加一位數(shù)（不進位）→兩位數(shù)加整十數(shù)→一位數(shù)加兩位數(shù)（不進位）和整十數(shù)加兩位數(shù)。每個任務承載不同的教學目標，呈現(xiàn)算理的程序表征、直觀表征、符號表征，并實現(xiàn)三類表征的貫通。

【關鍵詞】兩位數(shù)加一位數(shù)（不進位）;算理貫通;理法相融;學習路徑

一、問題提出

運算能力是最重要的數(shù)學素養(yǎng)。《〈義務教育數(shù)學課程標準（2011年版）〉解讀》指出：不僅會根據(jù)法則、公式等正確地進行運算，而且理解運算的算理，能夠根據(jù)題目條件尋求正確的運算途徑，稱為運算能力。只有理解了運算算理的運算能力才是真正具有生產(chǎn)性的[1]。同時，《義務教育數(shù)學課程標準（2011年版）》指出：“學生掌握數(shù)學知識，不能依賴死記硬背，而應以理解為基礎，并在知識的應用中不斷鞏固和深化。……在基本技能的教學中，不僅要使學生掌握技能操作的程序和步驟，還要使學生理解程序和步驟的道理。” [2]因而說，對于諸如整數(shù)加減乘除等運算類知識的教學，不僅要關注學生對運算程序、運算法則的掌握，還要關注其對算理的理解，這樣才能夠培養(yǎng)學生的運算能力。

兩位數(shù)加一位數(shù)，包括不進位與進位兩種情形，在整數(shù)加法中處于十分重要的地位。雖然在10以內的加法、整十數(shù)加一位數(shù)與整十數(shù)加整十數(shù)中已經(jīng)滲透了“計數(shù)單位相同的數(shù)才能夠直接相加”的概念，但是，此時的加法要么僅僅關注一個計數(shù)單位（10以內、整十數(shù)加整十數(shù)），要么通過數(shù)數(shù)就可以解決（整十數(shù)加一位數(shù)），事實上不涉及兩個計數(shù)單位，因而，計數(shù)單位的作用并沒有凸顯。兩位數(shù)加一位數(shù)，兩個計數(shù)單位的作用得到凸顯，因而，這是學生從“數(shù)位”的角度進行加減運算的開端，學生務必理解“計數(shù)單位相同的數(shù)才能夠直接相加”;同時，也是后續(xù)學習多位數(shù)加減法的重要基礎[3]。毫不夸張地說：兩位數(shù)加一位數(shù)學習后，再無“加法的相同數(shù)位對齊”。分析國內不同版本教材關于兩位數(shù)加一位數(shù)（不進位）、整十數(shù)的編排發(fā)現(xiàn)，人教版、北師大版、西師大版、蘇教版這四個版本教材在內容的組織上較為相似，都是以學生熟悉的生活場景作為情境圖，算理、算法上結合擺小棒，把兩位數(shù)加一位數(shù)（不進位）轉化為舊知10以內的加法和整十數(shù)加一位數(shù)。類似于這樣的口算過程圖，雖然是為了組織學生進行表象操作的過程——學生在頭腦中重現(xiàn)分一分、擺一擺的過程[4]，但又極容易給學生帶來不少的困惑。整體而言，雖然教材的結構是合理的、思路是清晰的，但問題是在實際教學中，有的教師要么特別重視算理的教學，通過多種方式呈現(xiàn)算理，但沒能夠實現(xiàn)算理的貫通，算理之間是互不關聯(lián)的;要么實現(xiàn)了算理的貫通，但沒有從算理水到渠成地走向算法。因而，必須探索有利于“算理貫通、理法相融”的學習路徑。

西蒙（Simon）認為教師作為一個領域的研究者，應按照學生的學習反思來修改教學活動[5]。Clements 與 Sarama 在Simon的理論基礎上，提出了學習路徑的概念，學習路徑就是對學生學習某一具體數(shù)學知識時思維與學習過程的描述以及一個相關的、設想的路徑，這個路徑由一系列的學習任務（Tasks）構成[6]。學習路徑不但可以把握學生在學習中是如何進步的，而且為教師設置合理的數(shù)學活動提供指導，有助于建立教與學的聯(lián)系[7]。

本文主要研究的問題是：（1）教師在教學中采用了怎樣的學習路徑？（2）存在哪些問題？（3）如何優(yōu)化學習路徑？（4）如何驗證學習路徑得到了優(yōu)化？

二、研究設計

（一）理論模型

本文將學生的理解分為以下3個類型（如表1），以這三類理解類型為標準來判斷學生對算理的理解情況。

（二）研究對象

授課對象是杭州市富陽區(qū)某小學一年級兩個平行班的學生，我們將這兩個班稱為甲班、乙班。根據(jù)學生的數(shù)學期末考試成績和前測數(shù)據(jù)，發(fā)現(xiàn)這兩個班級的學生在數(shù)學水平上沒有顯著性差異。授課教師為S。

（三）研究方法

本研究主要采用課堂觀察法、問卷調查法、訪談法以及行動研究法來收集數(shù)據(jù)。來自上課教師的數(shù)據(jù)包括：教學設計，教學錄像，教學后的反思日志，課前、課后對教師的訪談;來自學生的數(shù)據(jù)包括：前后測，課堂作業(yè)，訪談;來自教師發(fā)展指導者（即研究者）的數(shù)據(jù)包括：教學研討錄像。

我們通過課堂教學觀察及前后測數(shù)據(jù)的對比來說明學習路徑是否得到了優(yōu)化。前測和后測分別由2道題目組成，且前后測題目類型一樣。

先列式計算，然后用盡可能多的方法，如文字解釋、畫直觀圖、算式表示等來說明你的計算方法是合理的，說明得越詳細越好[9]。

（1）一雙鞋34元，一雙襪子5元，買一雙鞋和一雙襪子需要多少元？

（2）一張電影票45元，一瓶礦泉水3元，買一張電影票和一瓶礦泉水需要多少元？

（四）數(shù)據(jù)處理

根據(jù)學生的回答，對每種理解類型（程序理解、直觀理解、抽象理解）分別賦分，結果正確得1分，錯誤或未答得0分，并計算出不同理解類型的平均得分。

最終以學生理解水平的提升程度、學生的課堂表現(xiàn)和課后訪談為依據(jù)，探查兩位數(shù)加一位數(shù)（不進位）、整十數(shù)的學習路徑是否得到了優(yōu)化。

（五）實施步驟

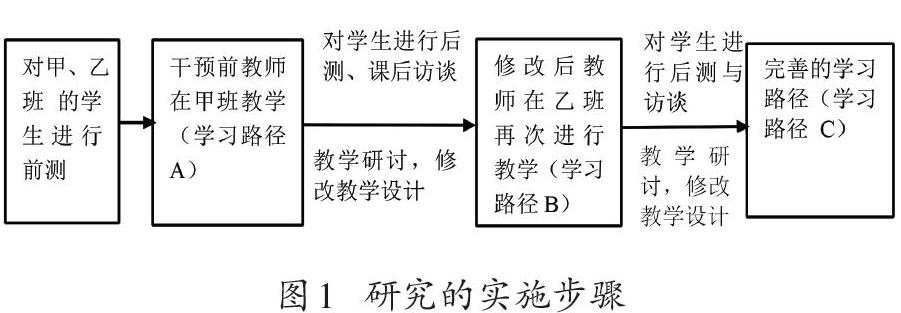
研究的主要步驟如圖1所示。

三、結果與分析

（一）學習路徑A

1. 學習路徑A呈現(xiàn)

教師在沒有任何干預的情況下獨立進行教學設計并授課。根據(jù)課堂實錄，整理出其設計與實施的學習路徑A，如圖2所示。

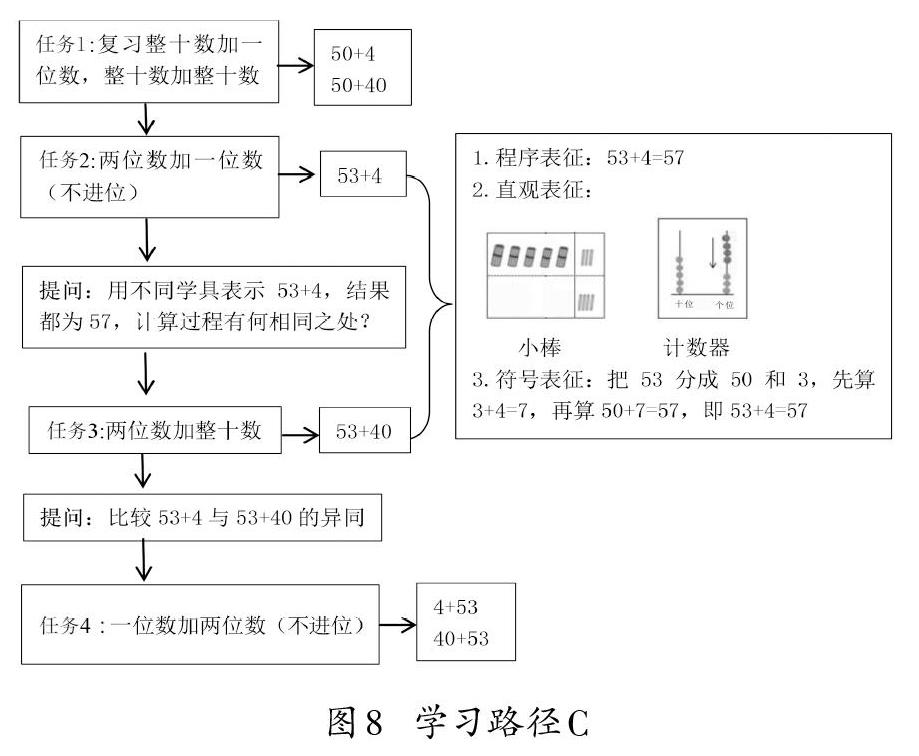
任務1意在復習“整十數(shù)加一位數(shù)”與“整十數(shù)加整十數(shù)”，為任務2做鋪墊。任務2意在促進學生對算理的理解，感知算法。任務3意在讓學生在理解算理的基礎上總結算法，凸顯相同計數(shù)單位上的數(shù)才能夠直接相加的算理。

2. 存在問題與原因分析

（1）沒有貫通算理

要真正理解算理，就要貫通各種表征方式，進而實現(xiàn)優(yōu)化。教師想通過多種方式來表征兩位數(shù)加一位數(shù)（不進位）的算理，但是各種表征之間并沒有貫通，而是孤立地存在。這種情況下，也許絕大部分學生能夠正確地進行運算，但是對于為什么這么算卻知之甚少。

師：請你在15+2=，20+15=，30+15=，這三個算式中選兩個進行研究，要求選擇的算式必須一個是兩位數(shù)加一位數(shù)、一個是兩位數(shù)加整十數(shù)。

師：請你根據(jù)探究單完成相應的任務。（探究單如圖3所示。學生小組討論，并完成學習單，時間持續(xù)11分鐘）

師：第一小組，你們的結果是怎么樣的？（學生呈現(xiàn)自己組的學習單，如圖4所示）

師：用小棒表示時，上面表示的是30，下面表示的是15。在數(shù)位表上，上面表示的是30，下面表示的是15。最后的分解圖，你有疑問嗎？（學生沉默）

師：老師有疑問，為什么要把30分成10和20？（學生沉默）

師：你們覺得是兩位數(shù)加整十數(shù)好，還是整十數(shù)加整十數(shù)好？

生：整十數(shù)加整十數(shù)好。

師：那我們在計算時，還需要把整十數(shù)分開嗎？

生：不需要。

師：那我們可以把30和15換下位置，把15分成10和5再計算。

首先，整節(jié)課大部分的時間讓學生來完成探究單，僅僅讓學生探究30+15=45這個算式就足足花了11分鐘。

其次，教師請學生擺一擺小棒、畫一畫數(shù)位表、撥一撥計數(shù)器后，僅僅呈現(xiàn)了算式和計算的結果，沒有要求學生說明為什么這么擺、這么畫、這么撥;黑板上也沒有留下各種可見的直觀表征。因此，也就談不上多種表征的貫通。

另外，由于教師把算式寫成了30+15=45，學生在寫分解圖時，出現(xiàn)了把30分成10和20的情況，學生困惑不已，教師不得不從各個角度引導學生，交換30和15的位置，從而使整節(jié)課的教學顯得尤為混亂。

（2）任務中的“數(shù)據(jù)”設計不合理

“15+2”“15+30”這兩個教學任務過于簡單，比如，學生通過“數(shù)手指”很容易就能算出“15+2=17”，這不利于學生探究算理。

3. 學習路徑完善建議

（1）促使表征貫通

教師在教學的過程中，除了讓學生動手操作外，還要向學生動態(tài)演示計算的過程，在黑板上要留下親眼可見的直觀圖，同時要注意表征的貫通。

（2）改變探究算式

增加任務的難度，把15+2，15+30換成53+4和53+40，使數(shù)據(jù)更具有探索性。

（二）重構的學習路徑B

1.學習路徑B呈現(xiàn)

教師S在乙班重構的學習路徑B如下（圖5）。

相對于學習路徑A，路徑B有以下變化：

①改變表征方式，促進表征貫通。通過擺小棒、計數(shù)器表征出53+4的計算過程;由于數(shù)位表與計數(shù)器本質上是一樣的，這里不再使用數(shù)位表。

②任務中的數(shù)據(jù)變?yōu)?3+4和53+40，難度增大，使得計算過程更具有探索性。

2.重構路徑的效果分析

（1）教學實況分析

①實現(xiàn)表征貫通。

師：請小朋友說一說他是怎么計算的。

生：53分成50和3，3加4等于7，50加7等于57。

（學生邊說，教師邊在黑板上呈現(xiàn)，如圖6所示）

師：計算的先后順序是？

生：先算個位，再算十位。

師：老師準備了小棒、計數(shù)器、數(shù)位表，剛才這個小朋友說的計算過程，你能利用這些學具演示一下嗎？

師：請你先思考，再擺一擺小棒、撥一撥計數(shù)器，然后和同桌交流。

師：我們請這位小朋友說一說他是怎么想的。

生：我選擇小棒，先擺5捆小棒，再擺3根小棒，因為是加4，所以在個位上再擺4根小棒，結果是57。（學生邊說邊演示）

師：還有其他方法嗎？

生：我選擇計數(shù)器，先在十位上撥5顆算珠，在個位上再撥3顆算珠，因為是加4，所以在個位上再撥4顆算珠，結果是57。（學生邊說邊演示）

師：那53+40怎么計算？

生：把53分成50和3，50加40等于90，90加3等于93。（學生邊說，教師邊在黑板上呈現(xiàn)，如圖7所示）

師：用小棒怎么表示？

生：同樣地，先擺5捆小棒，再擺3根小棒，因為是加40，所以在十位上再擺4根小棒，結果是93。（學生邊說邊演示）

師：用計數(shù)器怎么表示？

生：先在十位上撥5顆算珠，在個位上再撥3顆算珠，因為是加40，所以在十位上再撥4顆算珠，結果是93。（學生邊說邊演示）

②促使算理走向算法。

師：我們計算53+4時，加上的4表示？

生：表示4個一。

師：所以這時候4要和誰相加？

生：和3相加，結果是57。

師：在計算53+40時，為什么4不是和3相加？

生：因為4在十位表示4個十，3在個位表示3個一，計數(shù)單位不同，不能夠直接相加。

師：所以4要和誰相加？

生：和5相加，結果是93。

師：是的，只有相同計數(shù)單位上的數(shù)才能夠直接相加。

通過以上教學過程，學生明白，只有相同計數(shù)單位上的數(shù)才能夠直接相加，從而促使算理走向算法;同時，為理解“數(shù)位對齊”做好了鋪墊。

（2）課后測試結果比較

為了檢測路徑A、路徑B的實施效果，兩次教學前后都對學生實施了前后測，結果如表2、表3所示。

由表2可以看出，無論前測還是后測，學生程序理解的均分最高，直觀理解次之，抽象理解的均分最低。第一次教學干預后，絕大部分學生能夠準確算出得數(shù)，一大半的學生能夠進行直觀表征，少部分的學生能夠進行抽象表征。

由表3可以看出，學生程序理解、直觀理解的均分較高，抽象理解的均分最低。整體來說，在三種理解類型上，后測的數(shù)據(jù)要大幅度高于前測，也就是說，實施學習路徑B后，教學取得了一定的進步，說明學習路徑得到了優(yōu)化。

3.問題與改進建議

（1）增加關鍵問題提問

在學生通過擺一擺小棒、撥一撥計數(shù)器呈現(xiàn)了53+4的算理與計算過程后，教師可以提出以下關鍵問題：學具不同，結果都是57，計算過程有何相同之處？這樣可以幫助學生實現(xiàn)算理的貫通。同時，在計算53+40后，引導學生比較53+40與53+4的異同，促使算理走向算法。

（2）增加任務4

任務4是計算4+53，40+53，強化算法，讓學生深刻感受53+4和4+53，53+40和40+53的異同，在產(chǎn)生一系列的認知沖突后明白，無論是53+4還是4+53，其本質都是一樣的，都是“相同計數(shù)單位上的數(shù)才能夠直接相加”。同時滲透加法交換律，53+4是57，4+53也是57;53+40是93，40+53也是93，使學生體會到即便算式的形式改變了，但是本質沒有變;加數(shù)的位置變了，但結果沒有變。

四、結論與建議

（一）學習路徑的建議

學習路徑設計的重點是對算理進行多種表征，并貫通各種表征，實現(xiàn)對算理的概念性理解;同時，在理解算理的基礎上，通過探究實現(xiàn)算理與算法的融會貫通。而要做到這一點，就要設計層次遞進的、具有內在邏輯順序的學習任務序列，構建合理的學習路徑[10]。通過對學習路徑A、B的實踐，分析，反思與批判，從促進學生理解算理的視角出發(fā)，我們建議兩位數(shù)加一位數(shù)（不進位）的學習路徑可構建如下（圖8）。

（二）充分認識到理解算理的重要性

一年級學生剛接觸運算類的知識，思維還處于萌芽階段，教師在教學過程中一定要使學生知其然且知其所以然，切勿進行機械的重復訓練。通過多種表征的轉化，使算理和算法實現(xiàn)融會貫通，為后續(xù)運算知識的學習打下扎實的思維基礎。因此，教師不僅要求學生能夠達到正確進行兩位數(shù)加一位數(shù)（不進位）、整十數(shù)運算的學習目標，而且更要使學生意識到理解運算算理對提高運算能力的重要性。

參考文獻：

[1]教育部基礎教育課程教材專家工作委員會.《義務教育數(shù)學課程標準（2011年版）》解讀[M].北京：北京師范大學出版社，2012.

[2] 中華人民共和國教育部.義務教育數(shù)學課程標準（2011年版） [M].北京：北京師范大學出版社，2011.

[3] 張美菊.搭建“腳手架” 實現(xiàn)思維攀升：“兩位數(shù)加一位數(shù)、整十數(shù)”的教學嘗試與思考[J].小學教學參考，2020（2）.

[4] 盧江，楊剛.義務教育教科書教師用書數(shù)學（一年級下冊） [M].北京：人民教育出版社，2012.

[5]Simon， M. A.Reconstructing mathematics pedagogy from a constructivist perspective [J]. Journal for Research in Mathematics Education， 1995（26）： 114-145.

[6]Sarama， J.， Clements， D. H. Evaluation of a learning trajectory for length in the early years[J]. ZDM Mathematics Education， 2011， 43： 667-680.

[7]Szilágyi， J.， Clements， D. H.， & Sarama， J. Young Children's Understandings of Length Measurement： Evaluating a Learning Trajectory[J].Journal for Research in Mathematics Education，2013，44（3） ： 581-620.

[8]鞏子坤.有理數(shù)運算的理解水平及其教與學的策略研究[D].重慶：西南大學，2006：109-127.

[9] 鞏子坤，盧子苓，等.分數(shù)除以整數(shù)學習路徑優(yōu)化的實證研究[J].小學數(shù)學教師，2019（3）.

[10] 鞏子坤，俞飛丹，等.程序性知識視角下的小數(shù)乘小數(shù)學習路徑[J].小學數(shù)學教師，2017（12）.

（1.浙江省杭州市余杭區(qū)育才實驗小學? ?311110

2.浙江省杭州銀湖實驗小學? ?311400

3.杭州師范大學經(jīng)亨頤教師教育學院? ?311121）