無砟軌道不平順對行車安全性影響的可靠性分析

李再幃，雷曉燕，高 亮

(1.上海工程技術大學 城市軌道交通學院，上海 201620；2.華東交通大學 鐵路環境振動與噪聲教育部工程研究中心，江西 南昌 330013；3.北京交通大學 土木建筑工程學院，北京 100044)

軌道不平順是高速鐵路無砟軌道養護維修的重要工作，其狀態直接關系軌道結構在役服役性能，并對列車運行的安全產生直接影響。為了保證無砟軌道服役安全性，鐵路管理部門對軌道不平順控制從幅值與波長兩個方面展開，即通過控制幾何形位幅值限值[1]與軌道不平順譜[2]來有效地實現軌道狀態管理。但鑒于軌道不平順具有顯著平穩隨機特性[3]，其結構函數無法用明確解析式進行表達，使得上述兩種方法無法定量地表征高速列車行車安全的可靠性。因此，從軌道不平順隨機特性出發，研究軌道不平順對高速列車行車安全性的影響并明確相關的敏感性因素就顯得尤為重要。

現有國內外研究往往基于隨機振動理論、輪軌動力理論、時頻分析理論、結構可靠性理論等探究軌道不平順對高速行車的安全性影響，如文獻[4]分析了軌道隨機不平順在不同列車運行速度下軌道隨機振動響應特性，確定了相應隨機變量的統計分布類型；文獻[5]通過建立列車-板式無砟軌道-路基動力學模型，討論了軌道短波隨機不平順對輪軌系統動力學響應的影響；文獻[6]利用VAMPIRE動力學軟件，分析了不同類型的軌道隨機不平順對300 km/h高速列車運行平穩性和安全性的影響，確定了影響列車平穩性的激擾源；文獻[7]建立輪軌動力學模型，通過輸入隨機軌道不平順，研究了不同速度和線路條件下脫軌系數功率譜密度動力學分布特性；文獻[8]利用Wavelet-Wigner-Hough時頻理論和輪軌動力學模型，分析了軌道隨機不平順對輪軌系統服役可靠性的影響；文獻[9]采用響應面和Simpack動力學模型相結合的方法，研究了軌道隨機不平順對列車運行安全性的影響。這些研究對提高軌道結構役服役安全性起到了極大的促進作用，有力保障了高速列車運行品質。但值得注意的是，上述研究多是從定性的角度出發對相關因素影響進行研究，缺乏定量描述；而目前對結構服役安全的定量分析往往是通過結構可靠度來實現的，且在無砟軌道結構部件損傷分析[10]、彈條疲勞性能失效分析[11]、軌道板橫向穩定性[12]等研究中得到了一定的應用。

基于此，本文利用結構可靠度的相關理論方法，將響應面法與輪軌動力學理論相結合，通過建立相應的結構失效極限狀態方程，研究無砟軌道不平順對高速行車安全性的影響，從而實現定量地對軌道不平順狀態進行評估。

1 列車運行安全性的極限狀態

在輪軌系統中軌道結構服役狀態失穩的特征表現形式較多，如軌道主體結構(軌枕、道床、底座板、軌道板等)承載力不足失穩，脫軌系數和輪重減載率失穩等。由于既有高速鐵路無砟軌道結構設計的偏安全性，使得在使用限期內的結構主體一般均可滿足承載力的設計要求。因此，輪軌系統的狀態失穩多呈現輪軌動力失穩的特征，即可以通過相關的輪軌動力學評估指標來確定列車運行安全狀態。現行國內外標準中，脫軌系數和輪重減載率是主要的安全評價指標[13]，所以，本研究中將這兩個指標作為列車運行安全性評價的主要標準。

根據相關標準和文獻[9,14]，本文對軌道結構服役極限狀態定義進行界定：輪軌系統的一部分超過某一特定狀態就不能滿足相關鐵路設計規范的車輛-軌道系統安全行車的要求，該特定狀態即為極限狀態。

極限狀態實質上是列車運行安全狀態的一個閾值，在該閾值以內，處于安全而可靠的狀態；反之，若超過這一閾值，則處于不安全和失效的狀態。

如果用隨機向量X=(X1,X2,…,Xn)表示影響列車運行安全的n個基本隨機變量，用Z=g(·)表示列車運行安全狀態功能函數為

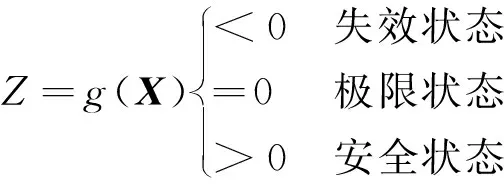
(1)

式中：“極限狀態”所對應的Z=g(X)=0為極限狀態方程。若對應脫軌系數和輪重減載率兩個評判準則有兩種失效狀態對應的列車運行安全性極限狀態方程為

(2)

(3)

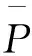
由式(2)和式(3)可知，這些功能函數受諸多因素影響(軌道不平順、外界環境等)，無法得到相應的顯示解析表達式，這就意味著無法進行相應的積分梯度運算來確定失效概率，因此，本文采用響應面與輪軌動力學模型相結合的方法進行狀態函數的隱式化研究。

2 響應面法原理與極限狀態方程求解

2.1 基本原理

響應面法(Response Surface Methodology, RSM)為解決極限狀態方程形式隱式化問題提供了一種可靠的建模及計算方法，其基本思想是對于隱式或需要耗費較多時間才能確定實際功能函數或極限狀態面，用一個相對方便應用的顯式函數(稱為響應面函數)代替，其基本算法如下[15]：

(1) 選擇包含不交叉項的二次多項式響應面作為響應函數為

(4)

式中：a,bi,ci為二次多項式的未知系數。

(2) 選取抽樣中心點xM=(x1,x2,…,xn)T，圍繞中心點利用試驗設計方法選取試驗點，即圍繞抽樣中心點選取2n+1個試驗點如下：

(5)

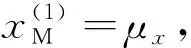
(6)

(3) 計算2n+1個抽樣點處功能函數值，計算第k次迭代時式(4)中二項式的待定系數，進而確定出第k次迭代時響應面模型的顯示表達式。

(5) 反復執行式(2) ～式(4)，直到前后兩次計算所得可靠指標之差|β(k)-β(k-1)|<εβ，εβ為預先給定的收斂準則，一般為0.000 1。

2.2 模型建立與求解

由式(2)和式(3)可知，需進行輪軌動力學計算，本文采用的模型為有限元法建立列車-無砟軌道-路基耦合動力學模型，相關的模型推導與驗證見文獻[1]，采用交叉迭代法進行系統動力學響應求解。

由于高低不平順和軌向不平順是輪軌作用力的主要來源，且兩者呈現不相關的關系[13]，因此，本文將此兩種不平順作為輪軌系統的輸入參量，輪軌力作為輸出參量，將其代入極限狀態方程中，采用響應面法進行求解，從而確定列車運行安全性。計算流程如圖1所示。

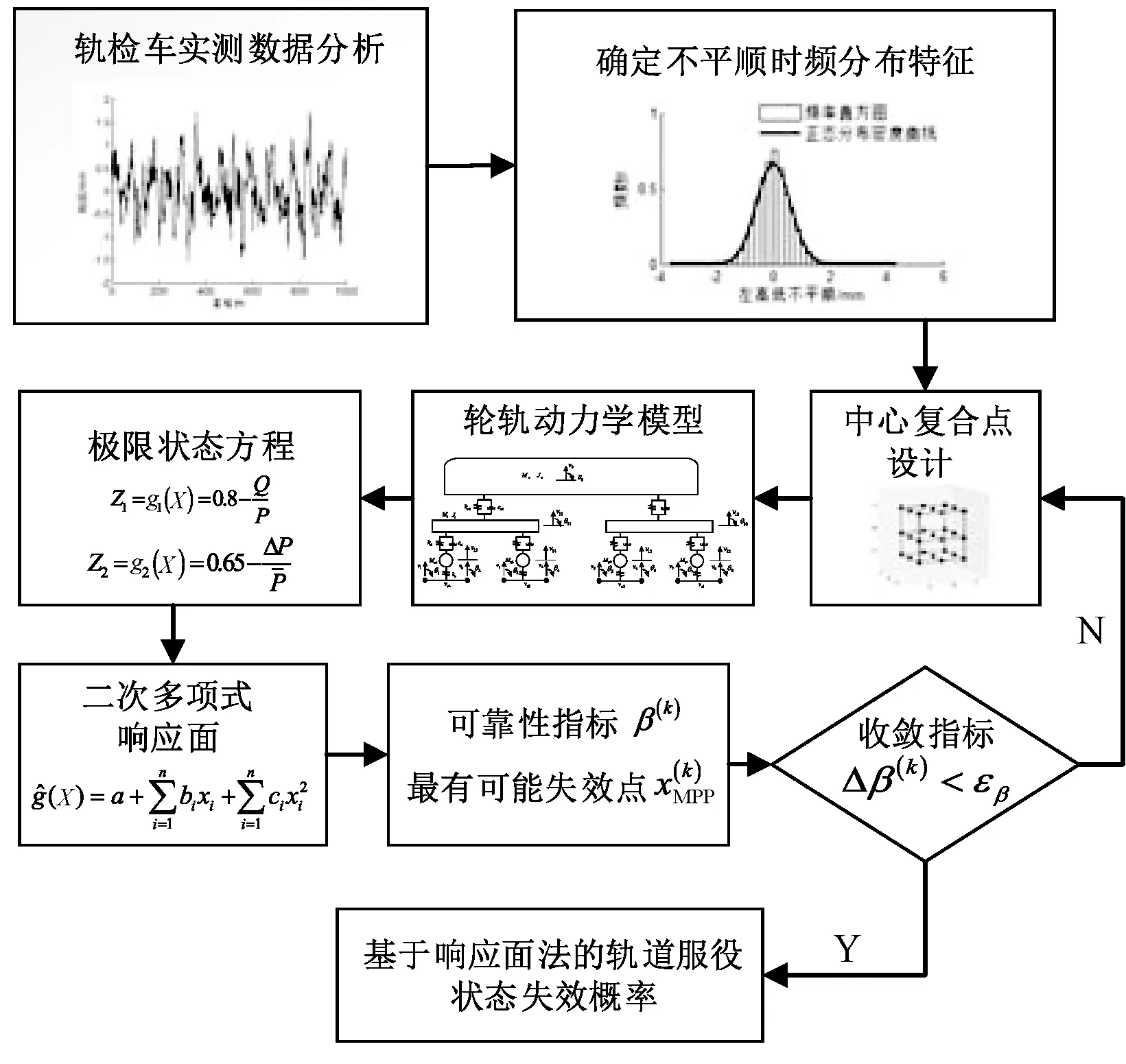
圖1 模型的計算流程

具體計算方法為：

(1)根據實測輪軌系統激勵源數據(高低不平順和軌向不平順)，計算樣本統計特征(均值、方差和概率密度函數)。

(2)將不平順樣本均值作為中心點，利用中心復合點法，生成不平順樣本值，計算相應的輪軌動力學響應。其中，f值采用自適應性調整的方法。為了涵蓋每個隨機變量的絕大多數信息，應用工程中的3σ原則，因此，第一次迭代計算時f取為3。為了減小樣本寬度對迭代收斂速度的影響，從第二步起f值取為1。

(3)采用式(4)作為響應面函數來逼近列車運行安全極限狀態方程，利用一次二階矩法計算可靠性指標β和最可能失效點MPP。

3 模型驗證與分析

3.1 算例

為了對本文所提分析方法進行驗證，這里采用如下算例：

高速列車為標準CRH3型動車組、運行速度為350 km/h，軌道結構為CRTSⅡ型雙塊式無砟軌道，基礎為路基結構，相關的參數值詳見文獻[1]。

軌道不平順實測樣本為0號高速綜合檢測車所測某高速鐵路線路數據，典型區段的檢測結果時域波形如圖2所示。

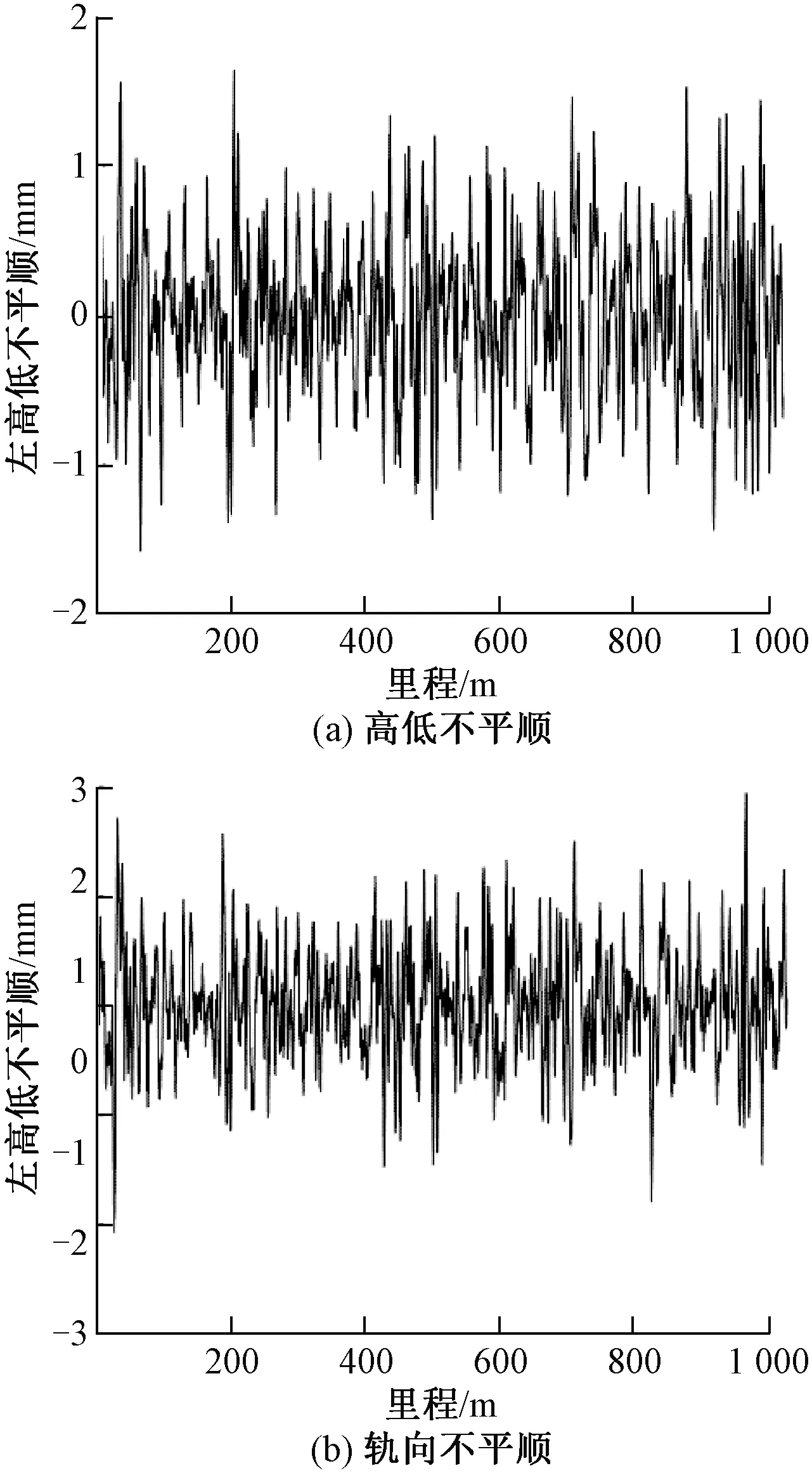
圖2 軌道不平順時域分布

采用中心線高低不平順和軌向不平順作為樣本輸入，則相應的實測樣本時域統計特征計算結果如表1所示。

表1 不平順統計檢驗與分布參數

由表1可知，軌道不平順在置信度0.05下，符合高斯分布，可利用其對相應不平順的概率密度函數進行描述。

將軌道不平順的統計特征值代入到響應面與輪軌動力耦合中，得到的軌道結構服役安全性計算結果，如表2所示。

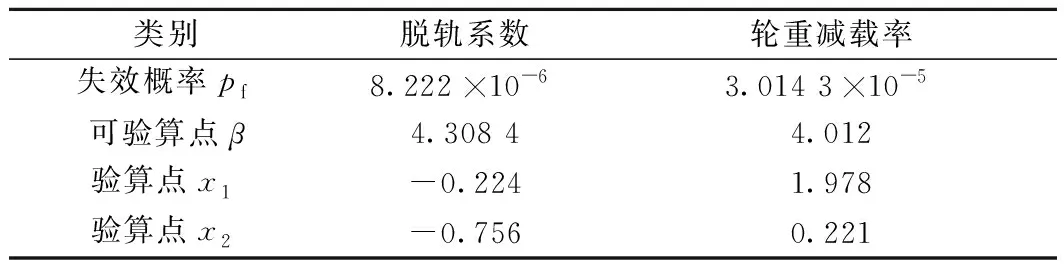
表2 RSM計算結果

根據GB 50216—2019《鐵路工程結構可靠性設計統一標準規范》[14]可知，CRTSⅡ型板式無砟軌道屬于鐵路工程結構安全等級中的二級，對應的目標可靠度指標建議管理值為3.7即失效概率為1.078 ×10-4，則表2中所得的區段樣本滿足可靠性技術標準的要求。

對比高速鐵路無砟軌道動態幾何不平順管理值[16]可知，最有可能失效點區間為[0, 2]mm即為350 km/h線路軌道Ⅰ級峰值管理值。

除了改善生態環境、塑造綠帶景觀外,環城綠帶植物群落的功能也需隨著城市更新而不斷豐富和完善。上海市綠化局牽頭研究編輯的《上海市綠道專項規劃》[4]中提到計劃在2020年于環城綠帶百米林帶內建設綠道,供市民進行日常活動。近年來,人們休閑娛樂需求日益增長,環城綠帶百米林帶因其區位條件好、消費成本低、交通便捷,將成為居民日常休閑活動的最佳去處[5]。然而目前針對上海環城綠帶植物群落的研究中,尚缺乏對于植物群落與游憩的相關研究。

3.2 模型驗證與分析

蒙特卡洛法(Monte Carlo Simulation，MCS)在樣本足夠大的情況下，可以有效地逼近非線性系統的解析解[15]。因此，本文這里采用MCS進行驗證求解，從而對上述計算結果進行驗算。相應的計算流程見圖3。

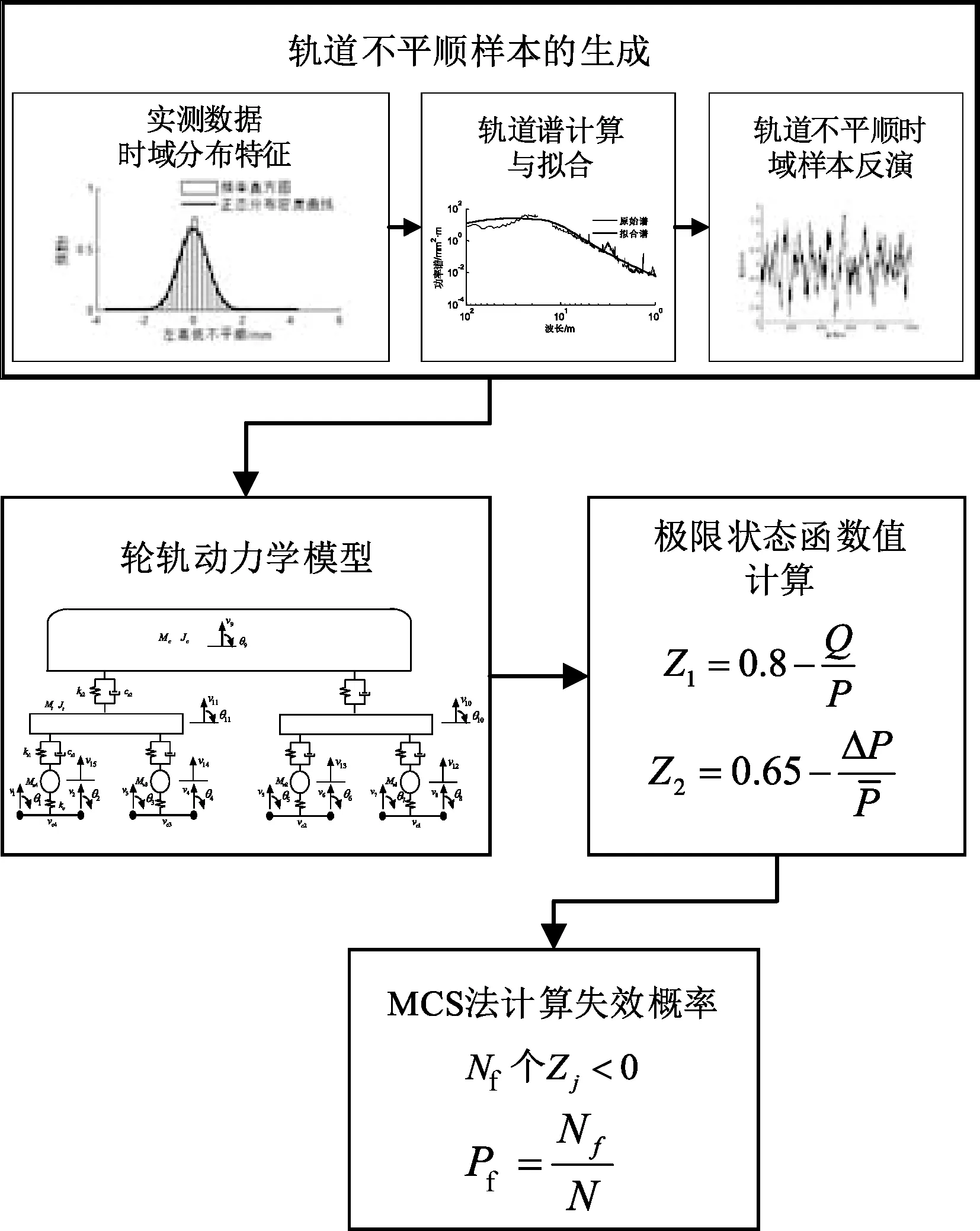
圖3 MCS法計算求解流程

利用圖2中實測的軌道不平順樣本進行軌道譜擬合，利用得到的擬合參數進行時域波形反演。將軌道不平順時域樣本作為激勵源輸入到輪軌動力學模型中，計算相應的軌道結構服役失效概率及可靠性指標。若要使得靠指標β滿足規范[14]的可靠度指標要求，則至少要進行1×105以上的次數，本文這里選取計算次數為1×105。則，得到的計算結果見表3。

表3 MCS計算結果

由表3可知，利用MCS方法得到的計算結果與表2相比差距很小，其誤差可以滿足工程計算的精度要求，這說明了利用響應面法求解列車運行安全極限狀態方程的準確性。

值得注意的是，由于本文輪軌動力學采用有限元方法，在形成軌道單元和車輛單元時，雖已經進行了相關的優化計算，但矩陣求逆仍需耗費大量時間。因此，進行一次1×106的MCS法機時巨大，一般為9.48×108s。而采用響應面法求解時，雖一般只需進行數十步迭代即可滿足可靠度指標的收斂條件，但每次動力學響應迭代計算仍需耗費大量的機時，一般為4.93×104s。所以，進行MCS方法計算時間為RSM方法的1.92×104倍。

綜上分析，可知采用響應面方法可以有效地實現列車運行安全極限狀態方程的求解，所得到結構的失效概率和可靠度指標與蒙特卡洛法得到的近似解析解相比較，符合度極高，說明了本文所提方法的有效性與準確性。

4 結論

本文通過建立無砟軌道結構服役安全極限狀態方程，采用響應面與輪軌動力學相結合的方法，研究了無砟軌道隨機不平順對高速列車運行安全性的影響，得到以下結論：

(2)可以采用響應面和輪軌動力學相結合的方法對列車運行安全性進行概率評價。

(3)在現有的軌道不平順狀態水平下，無砟軌道結構服役狀態可以滿足高速列車安全運行的要求。

(4)建議將可靠性分析納入到結構設計及養護維修中，以便更加全面有效地保證線路軌道結構的運營安全。