基于等裕度的60 kV油紙套管縱絕緣優化
劉道生,陳星蓉,趙子明
(江西理工大學 電氣工程與自動化學院高電壓與絕緣技術實驗室,江西 贛州 341000)
0 引言
油紙電容套管是變壓器的核心部件之一,作為變壓器出線裝置,其絕緣性能將直接影響到變壓器的穩定運行[1]。套管故障大多由絕緣部分在工作中不斷劣化或出現結構缺陷所致,如末屏放電和局部放電缺陷導致絕緣老化,以及電容屏間的熱效應等,最終導致絕緣擊穿,這些問題一直困擾著生產廠家,威脅現場設備的安全運行[2-5]。針對這些問題,應對套管絕緣結構進行優化設計,以提高其電氣絕緣性能。
絕緣結構的優化主要基于其電場分布計算,有限元數值分析是計算電容套管等復雜結構電場分布的有效手段之一[6]。文獻[7]基于有限元仿真分析,應用RBF神經網絡與NSGA-Ⅱ混合算法對套管的絕緣結構參數進行優化,使關鍵位置處的場強值達到最優;文獻[8-10]討論了交流復合套管和SF6充氣套管的內部屏蔽優化,獲得了理想的內外電位和電場強度分布;文獻[11]對油浸紙套管電容芯子極板邊緣進行優化,改善了邊緣場強分布;文獻[12]對油紙套管的瓷套進行優化,提高了均壓球表面及尖角電極附近區域的絕緣裕度。但以上設計方法均未涉及內部電容式芯子由其導桿到外屏的層間絕緣,即縱絕緣的電氣性能優化。文獻[13]對穿墻套管進行等裕度優化設計并進行場強分布計算分析,結果表明等裕度設計可提高穿墻套管的局部放電起始電壓和均勻內部絕緣電場分布。電容式套管的等電容與等裕度計算方法已有應用,但低局放油紙電容套管的等裕度設計優化及其相關計算分析,還需進一步研究。
本文對60 kV油紙電容套管的電容芯子設計方法進行討論,研究套管等裕度優化過程。利用ANSYS有限元仿真分析軟件對等電容、等厚度、等裕度3種設計方法下的套管芯子模型進行電場仿真,分析比較3種設計方法的電容芯子場強分布,得出最優設計方案。通過設計與制作等效模型對參數計算方法進行實驗驗證,證明等裕度優化設計方案的可行性。
1 油紙電容套管絕緣設計
目前在60 kV及以上電壓等級的高壓電力設備中,廣泛采用電容式套管,其在變壓器中起著引流、絕緣以及機械支撐作用。油紙電容套管的主要結構有上、下絕緣瓷套、法蘭(連接套筒)、內部電容芯子和其他附件,中心導電桿和法蘭之間的電容芯子作為套管的縱絕緣,決定著電容套管的整體電氣性能[14-15]。套管電容芯子的絕緣結構如圖1所示,其結構整體對稱,圖1中左側為套管芯子的剖視圖,右側為套管電容芯子主視圖。各層電容極板均包裹在絕緣紙內,用于強制均勻其內部電場分布,最內層極板緊貼導桿[16]。
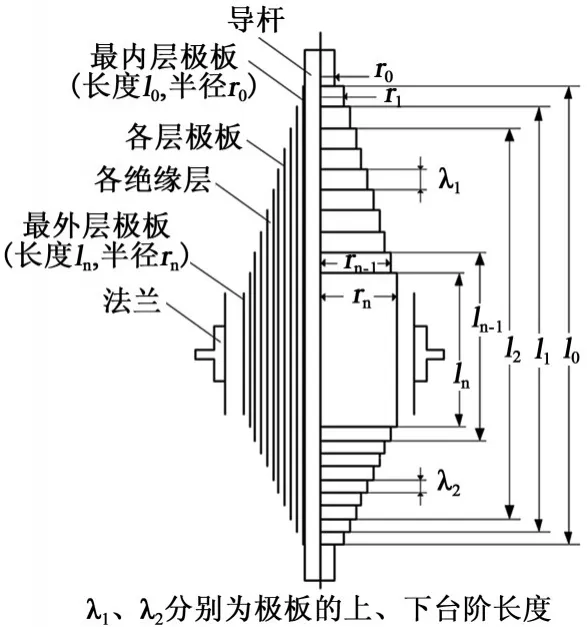
圖1 套管電容芯子的絕緣結構Fig.1 Insulation structure of capacitive core for the bushing
1.1 極板結構參數
電容芯子內部由導桿至外屏方向的徑向場強Er和芯子外部沿其階梯方向的軸向場強Ea都取決于電容芯子的各極板半徑和長度,合理設計各層極板的徑向與軸向尺寸可使套管芯子徑向與軸向場強均勻,并縮短套管半徑及長度[16]。
若忽略電容芯子中的邊緣效應,則各均壓極板通過的電通量不變,其基本關系為式(1)。

式(1)中:D為電位移量,C/m2;εr為絕緣材料的相對電容率;ε0為真空電容率,其值為8.854×10-12F/m;A為極板面積,m2;r為極板的半徑,m;l為極板的長度,m。
若保持徑向場強Er不變,則由rl=c(常數)可得式(2)。

由式(2)可知,Eα與r2成正比,使得軸向場強分布不均勻,套管設計長度過長,通常不選用該方案。
若保持軸向場強Eα不變,可得式(3)。

式(3)中:U為套管最大工作電壓,kV;l0為最內層極板長度,mm;ln為最外層極板長度,mm;r0為最內層極板半徑,mm;rn為最外層極板半徑,mm。
因為極板半徑r和長度l的變化相反,Er較為均勻,所以選用軸向場強不變的設計方法對高壓套管極板進行設計。
1.2 等電容絕緣結構
通過最小絕緣厚度設計,確定油中極板邊緣放電的電壓值,計算極板邊緣局部放電起始場強。根據設計絕緣裕度得出徑向最大許用場強,以此確定該電壓等級下電容套管的設計層數。在保證芯子上、下部位不發生軸向閃絡的情況下,根據上、下瓷套長度得出上、下臺階長度,以場強分布均勻和減小材料消耗為設計原則,計算出各層極板長度,以縮小套管整體尺寸。
實際生產中,通常采用等電容原則來設計極板半徑,使各絕緣層間的電容和電壓相同,絕緣層間的絕緣設計厚度不同[17]。
等電容設計時,任一層極板的電容值Ck如式(4)所示。
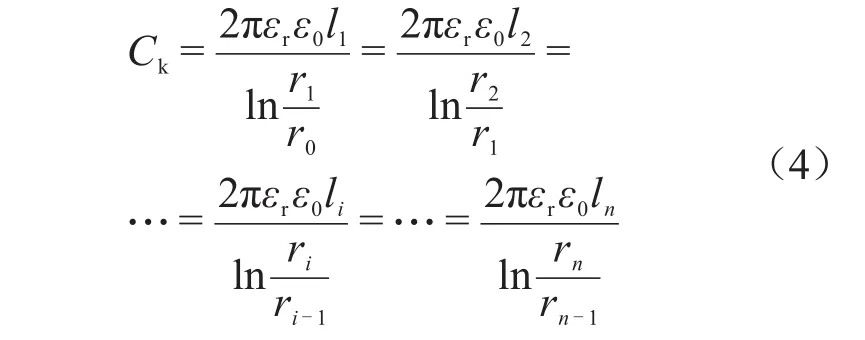
1.3 等厚度絕緣結構
等厚度設計使得每層絕緣極板厚度相同,每層局部放電起始電壓相同并高于等電容設計最小值,優化了邊緣兩側絕緣層的局放起始電壓。絕緣層厚度可由式(5)確定。

等厚度設計中,各層絕緣厚度相等,方便生產卷制,各層局部放電起始電壓相同,但各層電壓分布和局放裕度極不均勻。
1.4 等裕度絕緣優化設計
基于等電容和等厚度兩種設計方法,文中引出套管芯子的等裕度設計概念。套管內絕緣芯子的整體局部放電起始電壓主要取決于各絕緣層中的最小局放裕度。等裕度設計依據等電容設計原理,在芯子絕緣層數n不變,軸向場強Eα的分布及芯子整體尺寸不變的情況下,合理調整各層絕緣厚度,使各絕緣層所分擔的電壓和該絕緣層的局放起始電壓之比近似相等,即各絕緣層的局放裕度相等。提高電容芯子的整體局放起始電壓,保證套管設計的經濟合理性及可靠性[15]。
等電容設計下的套管芯子整體尺寸已確定,絕緣層數及各極板上、下臺階長度λ1x、λ2x已知,則電容芯子上部與下部軸向電場強度Eα1、Eα2分別為式(6)和式(7)。

式(6)~(7)中:U為套管最大工作電壓,kV。
由等電容設計原理所得的每一層極板的長度與半徑,作為等裕度設計中各層極板長度與半徑的初始值,由此得到每一層的電壓值ΔU、上下臺階長λ1、λ2以及第x層極板的長度lx,如式(8)~(11)所示。

當軸向場強Eα分布均勻時,套管極板的包絡線方程為式(11)。
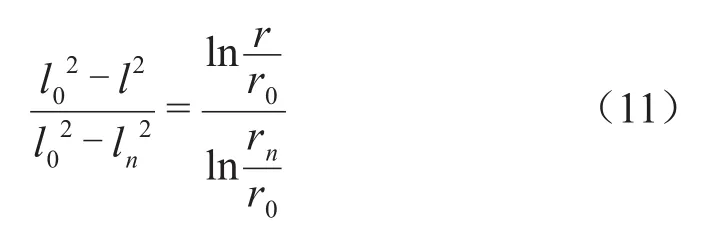
由式(11)解得各極板半徑rx為式(12)。
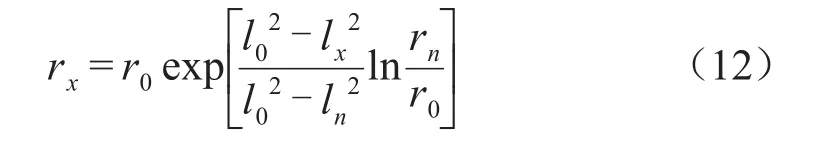
由式(3)可得該層徑向場強Erx為式(13)。
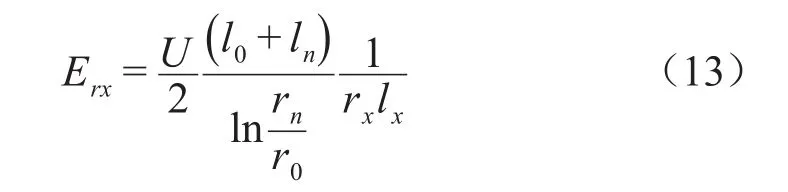
由式(13)可知,徑向場強的分布幾乎與絕緣厚度無關,按等裕度設計時的各極板徑向場強也幾乎不變。等裕度設計中,假設各極板處的徑向電場近似等于由初值計算的Erx,各絕緣層的局部放電起始電壓ΔUpx與工作時分配到該層的電壓ΔUx之比應為一常數,如式(14)所示。

式(14)中:Epx為第x層的局部放電起始場強,kV/mm;k1為油中極板起始局部放電時的經驗系數;dx為第x層的絕緣厚度,mm;εr為絕緣材料的相對電容率。將各層絕緣厚度之和表示為外屏與導桿半徑之差,并通過式(14)代換dx可得式(15)。

式(15)中:rn-r0為電容芯子絕緣厚度。由式(15)推導出常數A的表達式為式(16)。

計算并得到新的rx、Erx、lx、ΔUx、λ1x、λ2x。由式(14)得第x層絕緣厚度為式(17)。
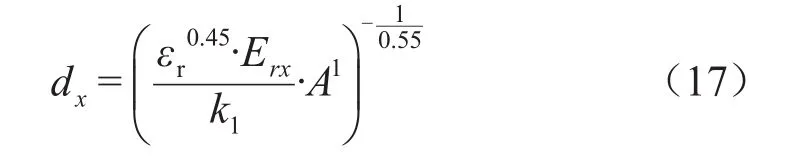
式(17)中:A1為式(16)的計算結果。更新后的各層極板半徑rx和長度lx分別為式(18)和式(19)。

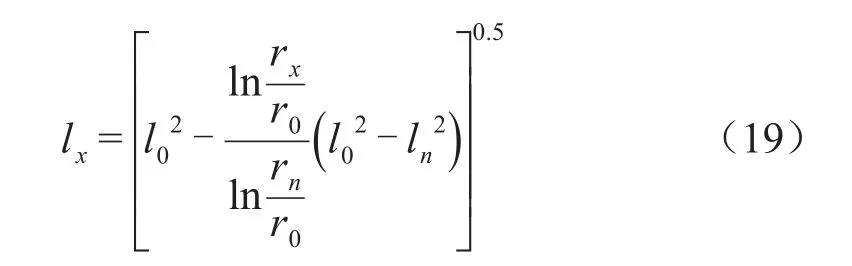
將更新后的極板半徑及長度代入式(13),重新計算Erx。其優化計算流程圖如圖2所示。

圖2 等裕度優化流程圖Fig.2 Flow chart of equal-margin optimization
等裕度優化設計中,經過循環計算后各絕緣層裕度的優化效果如圖3所示。
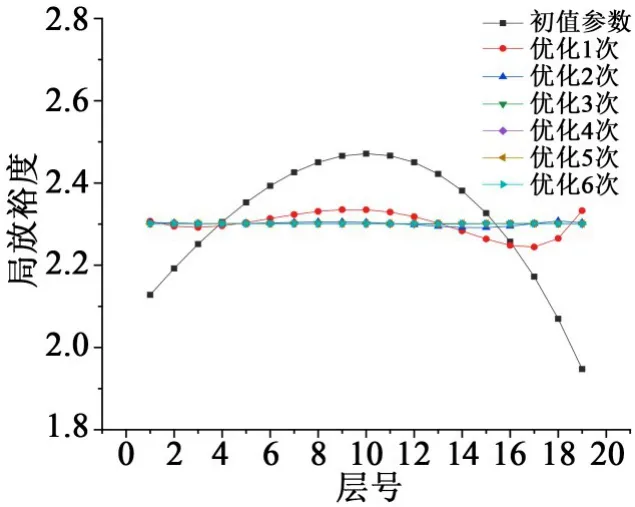
圖3 套管芯子絕緣層的局放裕度優化圖Fig.3 Optimization diagram of partial discharge margin of bushing core insulation layer
圖3表明,隨著優化次數的增加,絕緣層的局放裕度分布從初值參數的拋物線分布,逐漸變化為優化6次時的水平直線分布,即各層局放裕度趨近同一值,且各極板尺寸變化越來越小,直至電容芯子各絕緣層裕度值相等。等裕度設計中,各層局放裕度都相等且高于等電容和等厚度設計中的最小局放裕度,而電容芯子整體的局放起始電壓與最小局放裕度有關,因此能提高套管的局部放電起始電壓。
2 套管電場仿真分析
套管結構具有高度對稱的特點,其內部層間絕緣電場分布具有二維軸對稱結構。因此將三維套管模型簡化為二維軸對稱模型,將三維電場化為二維電場進行分析,且對計算精度和結果影響不大[18]。
采用ANSYS有限元仿真分析軟件,針對套管內部絕緣結構與關鍵尺寸建立有限元模型,并對套管內部電勢和電場分布情況進行分析,獲得套管的電勢和電場分布規律[18-19]。為模擬電容套管正常工作時內部芯子的電場分布情況,在中心銅棒上施加60 kV電壓,末屏及邊界法蘭處為零電位;為保證油浸絕緣紙中的金屬極板正常工作,在各層極板處添加懸浮電位。模型分析中主要材料的相對介電常數如表1所示。

表1 材料的相對介電常數Tab.1 Relative permittivity of the materials
套管場強分布如圖4所示,沿圖路徑a-b的徑向場強分布曲線如圖5所示。圖5中最左側為金屬導電桿,其內部場強基本為零,導桿上下兩端與絕緣油接觸,油中場強上升。絕緣層中介質為油浸絕緣紙,電場分布為中間低兩側高。
3種設計方法得到的套管的徑向場強分布如圖6所示。從圖6可看出,3種套管的徑向場強分布規律相同,但等電容設計的套管徑向場強分布不均勻,尤其是在最外層極板處電場畸變較大;等厚度設計的套管徑向場強在最外層處分布更為均勻,但最內層與最外層場強差距過大,導致絕緣內部場強分布不均;而等裕度設計的套管徑向場強分布比前兩者都更為均勻,且場強峰值有所下降。
在導桿中加載電壓,得到其局部放電起始場強最大值,與理論計算值進行對比,結果如表2所示。從表2可以看出,理論計算結果與仿真結果相符。
根據表2可知,等裕度設計方案將60 kV油紙電容套管的整體局部放電起始電壓在等電容設計的基礎上提高了12.36%。

圖4 套管芯子浸于油中工作時的電場分布Fig.4 Electric field distribution of bushing core immersed in mineral oil
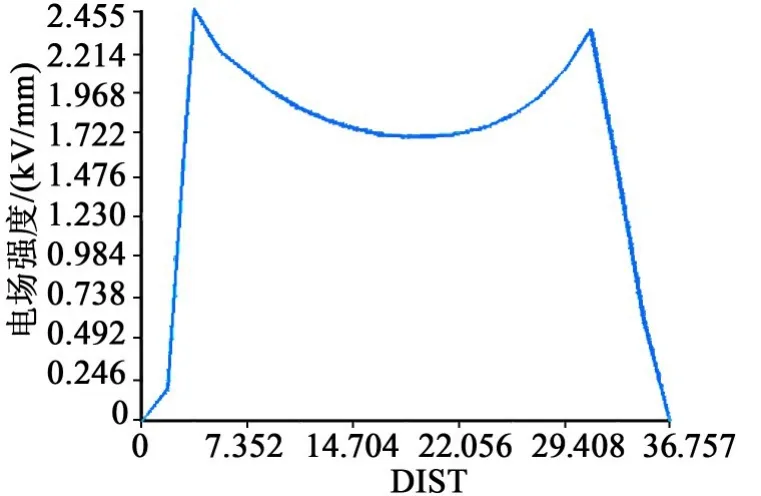
圖5 徑向場強分布曲線Fig.5 Radial field intensity distribution curve

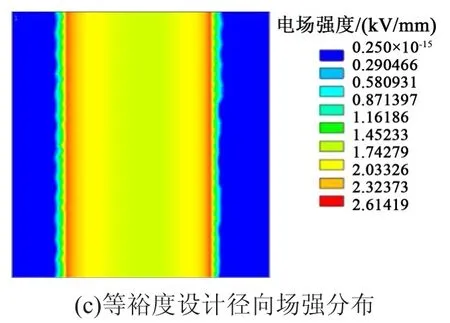
圖6 套管的徑向場強分布圖Fig.6 Radial field intensity distribution patterns of bushings
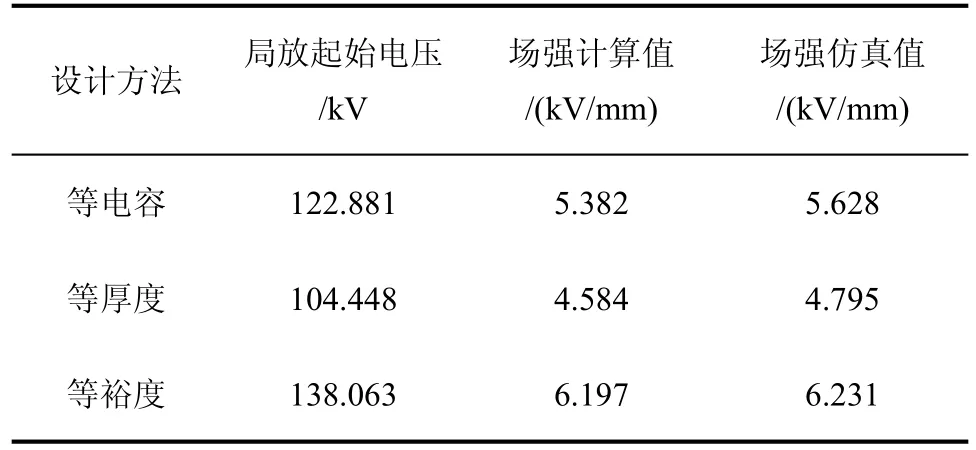
表2 局放起始電壓和場強的計算與仿真結果Tab.2 The calculation simulation results of initial partial discharge voltage and partial discharge field intensity
3 等效模型實驗
3.1 模型制作
依據前文所述設計方案和計算步驟,設計出等電容、等臺階、不同絕緣層厚度結構的電容芯子模型,使其結構參數和場強分布與實際60 kV模型等效。等效模型采用手工卷制,按照計算出的結構參數,控制極板長度和半徑。卷制時將銅箔電極和電纜紙交替纏繞在直徑為6 mm的銅導桿上,絕緣層采用厚度為0.01 mm的電纜紙纏繞而成,達到各絕緣層設計厚度要求為止。
3.2 實驗數據測量及分析
模型制作完成后進行真空干燥48 h,之后用變壓器油浸漬,除去套管芯子與容器內水分和氣泡,干燥溫度為105℃,真空度為50 Pa。干燥處理后的模型如圖7所示,等效芯子模型浸于變壓器油中,容器外部銅箔模擬實際套管外部法蘭,以方便測試時接地。通過對等效模型的電壓值、電容值及場強分布進行實驗測量,驗證模型參數計算的合理性與正確性。
芯子的電容值采用高壓介質損耗測試儀測量,測量電路采用正接線法,如圖8所示。

圖7 等效實驗模型Fig.7 Equivalent experimental model

圖8 電容測量正接線圖Fig.8 Positive circuit diagram of capacitance measurement
層間電壓測量中施加電壓為模型折算的實際工作電壓19.4 kV,所測電壓為各層極板對地電壓,測量接線圖如圖9所示。
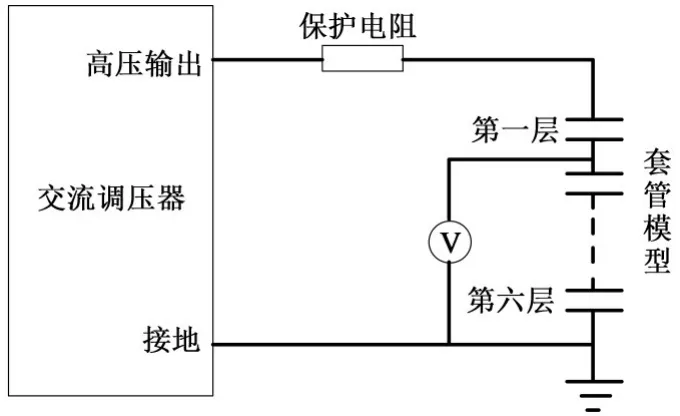
圖9 層間電壓測量接線圖Fig.9 Circuit diagram of interlayer voltage measurement
模型測量電容值如表3所示。從表3可以看出,3次實驗測量值與理論計算電容值相差不大。
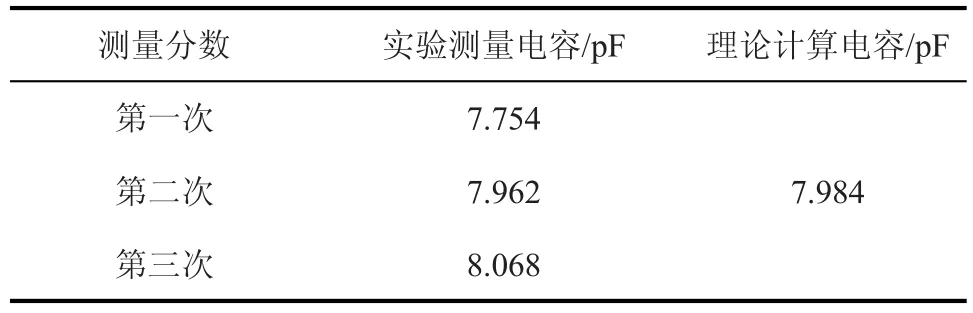
表3 電容測量結果Tab.3 Capacitance measurement results
模型各層電勢分布如圖10所示。從圖10可以看出,實驗值與計算值相比相差不大,皆由內至外呈線性下降。
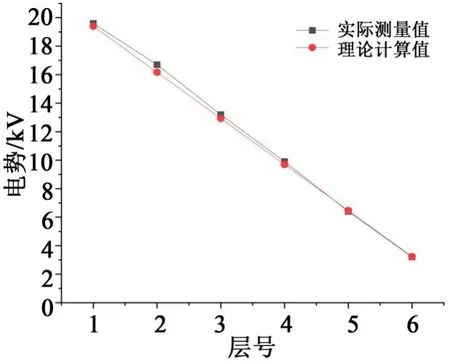
圖10 層間電壓測量結果Fig.10 Measurement results of interlayers voltage
等效模型中,由實測電壓得出各絕緣層的場強分布結果如圖11所示,電容芯子的外屏與內屏的場強較高,中間部分場強較低。實測電壓與計算電壓之間存在差異,但實測場強與計算場強分布規律相同且數值相近。說明本文的計算方法可行,各項參數符合套管實際運行工況。
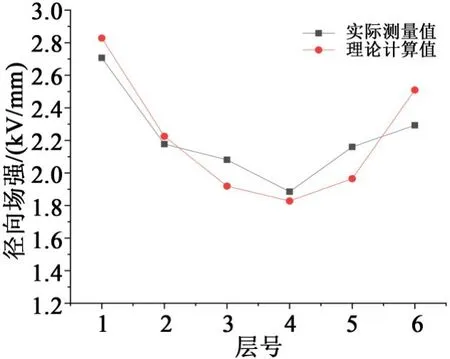
圖11 場強測量結果Fig.11 Field intensity measurement results
4 結論
(1)等裕度優化設計使套管芯子各絕緣層的局放裕度相同,且高于等電容設計的最小局放裕度。在60 kV油紙電容套管原設計基礎上,使其局部放電起始電壓設計值提升了12.36%。
(2)通過有限元計算分析和等效模型試驗可知,等裕度優化設計提高了套管電容芯子的局放起始電壓,優化了芯子徑向場強分布,驗證了套管模型參數計算的合理性。

