高速鐵路周期性橋梁頻域有限元法及墩底動反力分析

曹艷梅，楊 林，李東偉

(北京交通大學 土木建筑工程學院，北京 100044)

近年來，橋梁結構已成為高速鐵路的一種重要結構形式，如我國廣珠城際鐵路中橋梁占比超過了90%；京滬鐵路全長1 318 km，而橋梁總長達到1 060 km，約占80%[1]。因此，快速準確地得到移動列車荷載作用下橋梁結構的動力響應以及作用到承臺基礎頂面的動力荷載對高速鐵路橋梁的設計以及橋梁周圍場地振動的預測分析具有重要意義。

我國高速鐵路橋梁中，85%以上采用等跨徑布置的預應力混凝土簡支箱梁橋[1]和板式無砟軌道結構[2]，這種連續布置的結構具有一定的周期性，且其縱向沿兩端近似無限延伸，因此可采用無限周期理論對其進行分析[3]。劉維寧等[4-5]基于動力互等定理并通過Laplace變換和傳遞矩陣法研究了周期支承軌道對移動荷載的動力響應。Chebli等[6]利用Fourier變換將周期性結構對移動載荷的動力響應進行了研究。馬龍祥[7]將無限軌道動力響應的求解問題映射于軌道結構的一個基本元內，利用無限周期結構理論在頻域內推導了移動諧振荷載作用下軌道結構的動力響應。Hoang等[8]首先利用支承反力的周期性條件和Fourier變換建立了移動荷載作用下支承反力和梁位移之間的關系式，進而考慮了周期性支承為非線性的情況，并與線性支承下Timoshenko梁的動力響應進行了對比，給出了梁模型的適用情況[9]。在橋梁結構領域，沙萱[10]建立了移動荷載作用下缺陷周期性高架橋的樁-土-結構耦合模型，求解了橋梁結構的動力響應；陸建飛等[11]基于周期條件利用有限元法和Fourier變換建立了周期性高架橋頻域有限元模型，分析了橋梁結構在單個移動簡諧荷載作用下的動力響應，在其模型中對相鄰兩片主梁和橋墩接頭之間的阻尼效應考慮的較少，使得中低速移動荷載作用下的計算結果有一定的誤差；Shi等[12]采用周期性理論分析了板式軌道結構對橋梁豎向動力反應的影響[2]，并結合容積法分析出了高速鐵路高架橋板式軌道引起的地面振動特征頻率。

本文在前人研究的基礎上，基于無限周期結構理論建立橋梁結構頻域有限元模型，考慮高速列車運行時輪軌動力荷載的加載情況，提出先計算橋梁基本跨等效結點荷載矢量時程，再利用Fourier變換得到等效結點荷載矢量頻譜的方法，進而求解了不同加載頻率的移動荷載列作用下橋梁結構任意跨的動力響應和墩底的動反力。

1 周期性橋梁結構頻域有限元方法

1.1 周期性橋梁結構分析模型

以高速鐵路中常用的等跨徑布置橋梁結構為研究對象，移動荷載作用下周期性橋梁結構力學模型示意見圖1。該結構滿足周期性結構的特點，其周期單元由半跨左梁、半跨右梁和橋墩三個構件以及梁-梁-墩(Beam-Beam-Pier，BBP)接頭組成。該模型中由于考慮了軌道結構對相鄰簡支梁的連接約束作用，因此主梁和主梁之間的連接通過彈簧-阻尼元件進行模擬。本文將圖1的一個周期單元定義為基本跨(長度記為L)，墩底設為固端約束，基本跨的兩個端截面分別為左梁的跨中截面和右梁的跨中截面，端面分別受到相鄰跨梁體對其產生的軸力N、剪力Q和彎矩M，坐標原點定義為基本跨左梁跨中截面的形心位置。設梁上作用有豎向荷載P(x,t)和水平向荷載F(x,t)，荷載的移動速度為V。

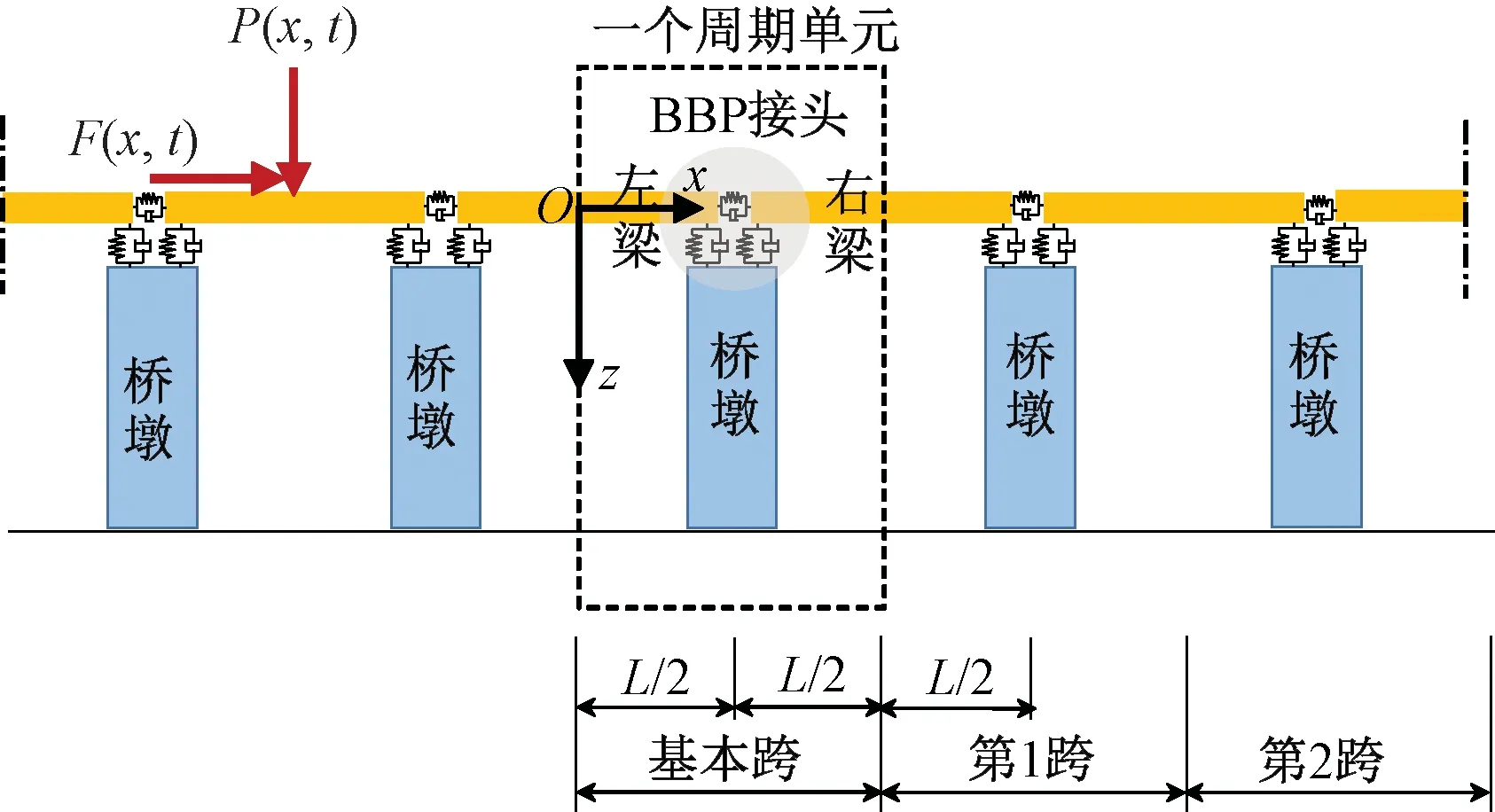
圖1 移動荷載作用下周期性橋梁結構力學模型示意

取基本跨為研究對象，根據結構動力學的知識，可得主梁(或橋墩)在時域內的軸向和平面內彎曲振動方程分別為[13]

(1)

(2)

式中：u(x,t)、v(x,t)分別為梁(或墩)的軸向、垂向位移；E為梁(或墩)的彈性模量，MPa；A為梁(或墩)的截面面積，m2；I為梁(或墩)的截面慣性矩，m4；ρ為梁(或墩)的密度，kg/m3；F(x,t)和P(x,t)分別為橋梁主梁所承受的水平動荷載和豎向動荷載。

對式(1)和式(2)的兩邊同時做Fourier積分變換，將其從時域內轉化到頻域內(在物理量上方加“-”表示)，可得

(3)

(4)

式中：E*=E(1+iη)為考慮了梁(或墩)的材料損耗因子η后的復彈性模量。

1.2 建立基本跨結構的動力方程

將基本跨的梁、墩構件離散為兩結點的梁單元，若構件α的單元數為E(α)，則構件α的結點個數為N(α)=E(α)+1，其中上標α=bl、p、br分別表示基本跨中的左梁、橋墩、右梁。若每個結點考慮三個自由度，基于式(3)和式(4)根據虛功原理，則可推得離散單元在頻域內的動力方程[14-15]為

(5)

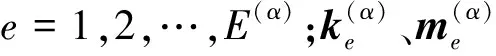
(6)

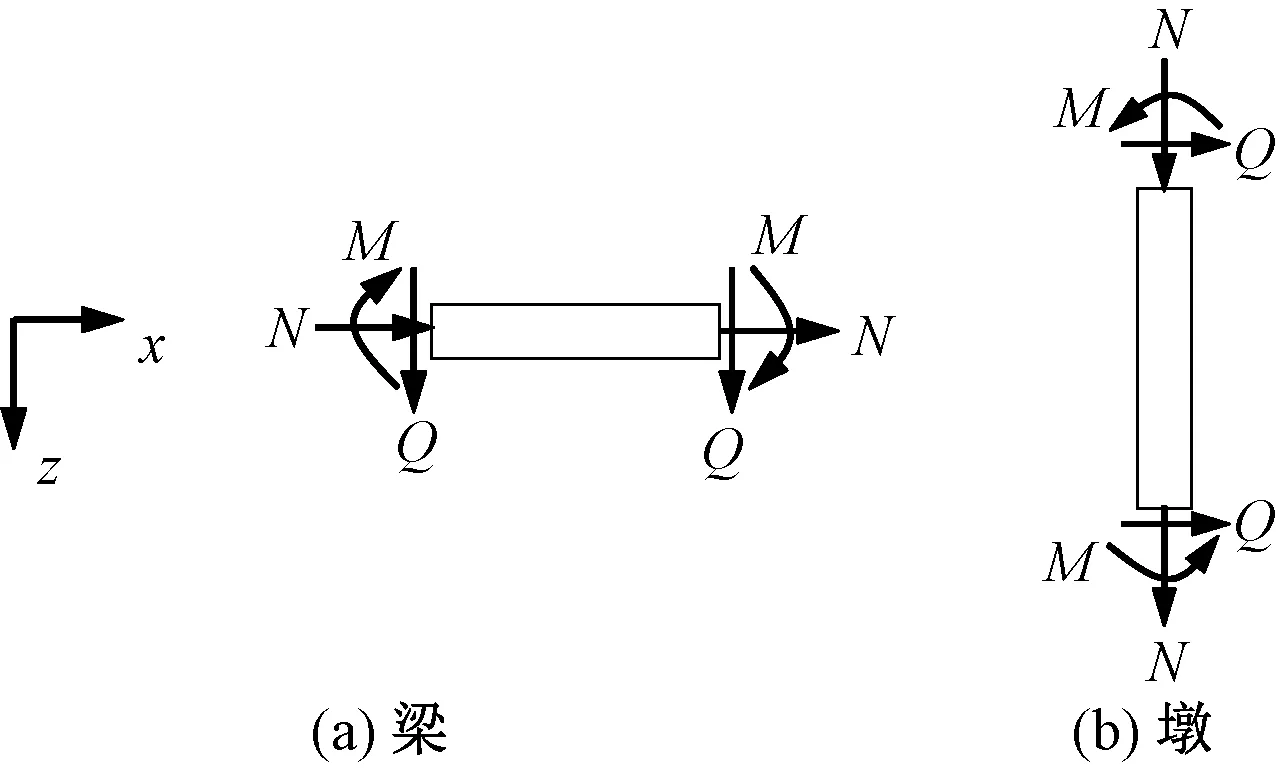
圖2 主梁和橋墩的單元結點力正向規定

對構件的單元剛度矩陣和質量矩陣進行組裝，可得到梁(或墩)整個構件在頻域內的動力方程為

(7)

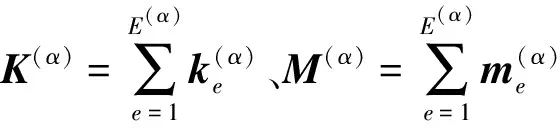
(8)

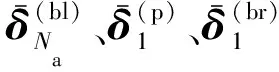
(9)

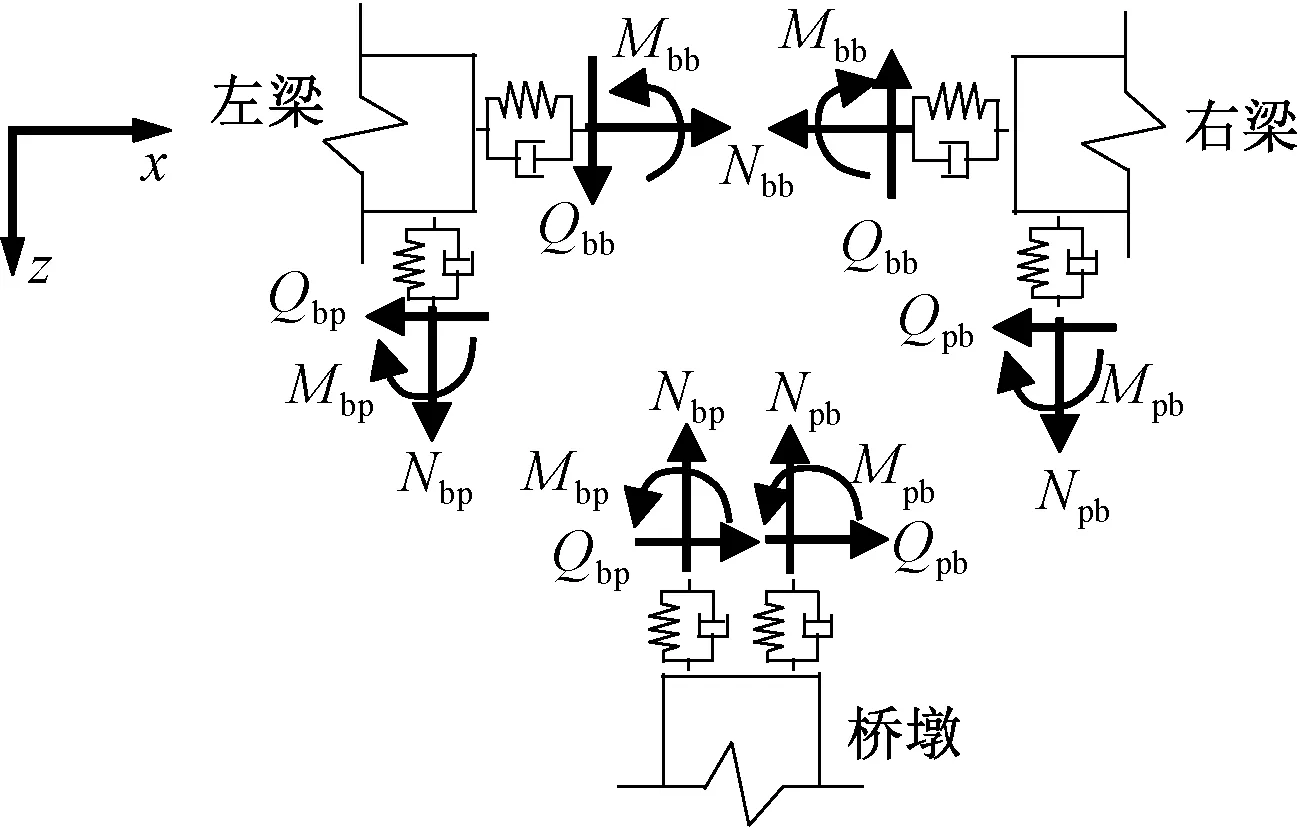
圖3 BBP接頭位置處彈簧-阻尼系統產生的內力

式中：Γ為BBP接頭位置處彈簧-阻尼系統的剛度矩陣。

若用k(t)、k(s)、k(b)分別表示BBP連接彈簧-阻尼體系的抗拉、剪切、彎曲剛度，則Γ的各子矩陣的具體表達式為

(10)

(11)

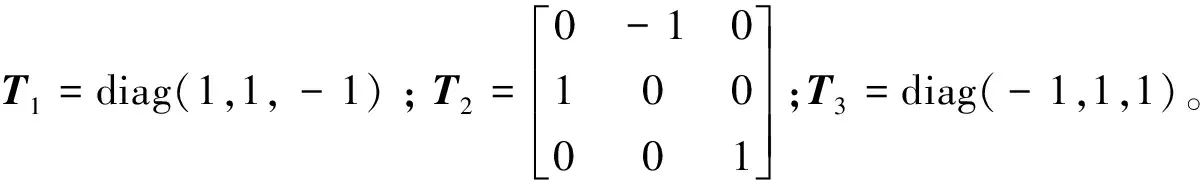
將式(9)代入到式(11)中可得BBP位置處結點力向量與結點位移向量之間的關系為

(12)

式中：矩陣S為BBP接頭位置截面的結點力與結點位移的關系矩陣，可由k(t)、k(s)和k(b)求出。

通過組裝各個構件的質量矩陣、剛度矩陣和阻尼矩陣，可得基本跨整體結構的動力方程為

(13)

1.3 邊界條件的引入及移動加載的實現1.3.1 墩底固結邊界條件的引入

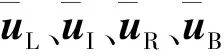
(14)

(15)

1.3.2 周期性邊界條件的引入

根據無限周期結構理論可知[8]，在激振頻率為ωp的簡諧荷載作用下，橋梁結構基本跨左端截面和右端截面的位移和集中力向量分別為

(16)

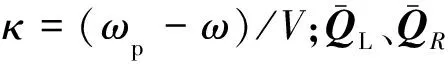
將式(16)代入式(15)中，可得

(17)

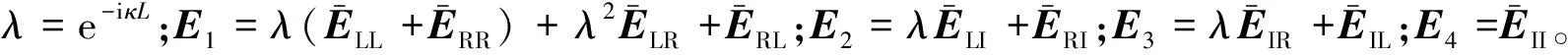
1.3.3 頻域內移動加載的實現

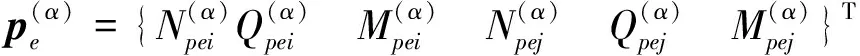
(18)

式中：L0為梁單元的長度；x為作用力距離該單元i結點的距離。

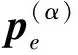
1.4 橋梁結構任意跨的動力響應求解

在求得橋梁結構基本跨的頻譜、時程動力響應后，基于無限周期結構理論可求解第n跨的動力響應為

(19)

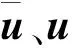
1.5 橋梁結構特征方程的推導

(20)

對式(20)進行整理，可得

(21)

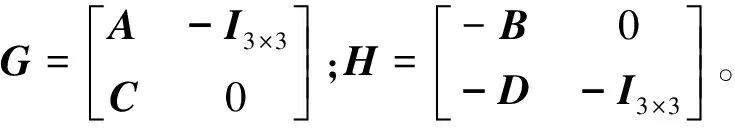
將式(21)和式(16)進行聯立，可得周期性橋梁結構自由振動的特征方程為

(22)

式中：κe為在周期性橋梁結構中傳播的特征波復波數，實部表示特征波相位的改變，虛部表示特征波的衰減；V為響應的特征向量。

2 頻域有限元方法的驗證

為驗證周期性橋梁結構頻域有限元方法的正確性，采用與文獻[16]相同的橋梁結構參數和荷載參數，將本文計算出的橋梁結構基本跨左端部豎向位移響應與該文獻中簡支梁跨中位移響應的解析解進行對比分析。

計算中，車輛參數為5節，每節車有兩個軸重，每個軸重荷載為215.6 kN。荷載列考慮為常力輪軸荷載，每節車車身長度為24 m，車身前后兩個軸重間距為18 m，前后兩車相鄰軸間距為6 m。梁體、橋墩有限元離散單元L0取0.2 m；若分析頻率和采樣點數分別為fs和N′，則頻率間隔取為df=fs/N′，分析時間t=1/df；時域分析中，時間離散點數NT=2N′，時間步長dt=t/NT。采用Matlab編程進行計算，不同列車速度下橋梁模型數值解與文獻解析解對比結果見圖4。

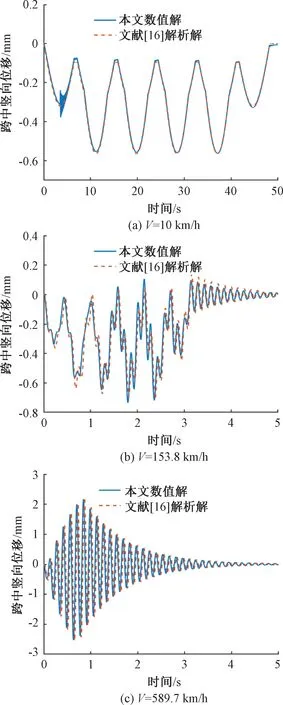
圖4 不同列車速度下橋梁模型數值解與文獻解析解對比

由圖4可知，本文模型的數值解與文獻中解析解在時程曲線的波形和振幅上基本保持一致，說明本文建立的周期性橋梁結構頻域有限元模型在求解橋梁結構動力響應是正確且有效的。

3 高速鐵路周期性橋梁結構的能帶特征及墩底動反力分析

3.1 模型參數

以鄭萬高速鐵路32 m預應力混凝土簡支箱梁(通橋〔2016〕2322 A)為算例，現澆實體橋墩高度為14 m，梁體和橋墩的材料與幾何參數見表1。支座模型中采用鐵路常用跨度簡支梁球形鋼支座，BBP接頭處的剛度阻尼系數取值見表2。高速列車采用8輛ICE3動車編組，輪軸荷載分布示意見圖5，固定軸距為2a=2.5 m，2b=14.875 m，兩鉤之距為l=24.775 m，靜軸重為P0=160 kN。

3.2 周期性橋梁結構的能帶分析

為了分析周期性橋梁結構的特性，首先根據1.5節的內容對其進行特征分析。經計算，該橋梁結構的前三階特征波波數隨頻率的變化見圖6。根據周期性結構特征波波數隨頻率的變化情況，可以觀察其能帶特性，波能傳播的頻帶稱為通帶，即實部不為零的頻帶，反之稱為禁帶[17]。周期性結構具有一定的隔振性能，當具有一定頻率范圍的波動傳播至周期性結構時，只有通帶內的頻率可以通過，而禁帶內的頻率將被阻隔。

圖5 ICE3動車車輛輪軸荷載分布示意

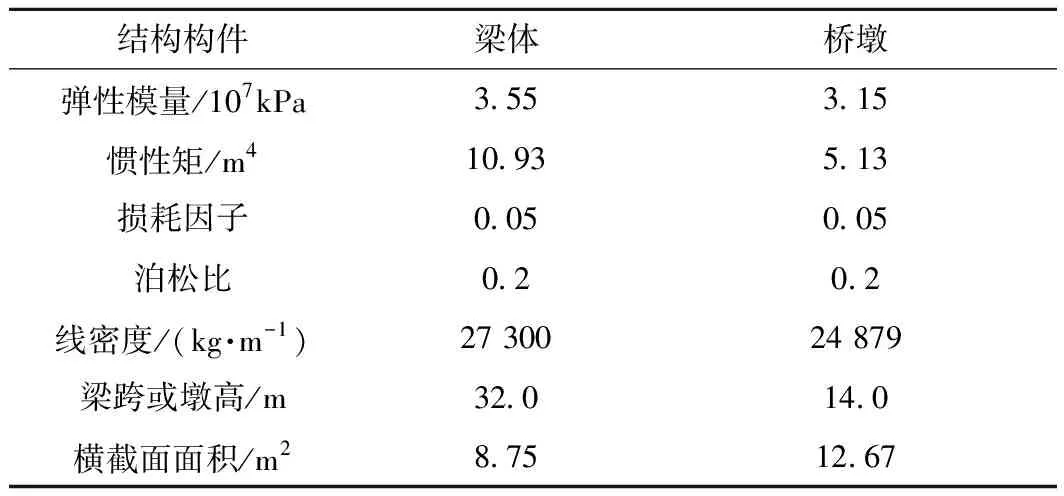
表1 梁體和橋墩的材料與幾何參數

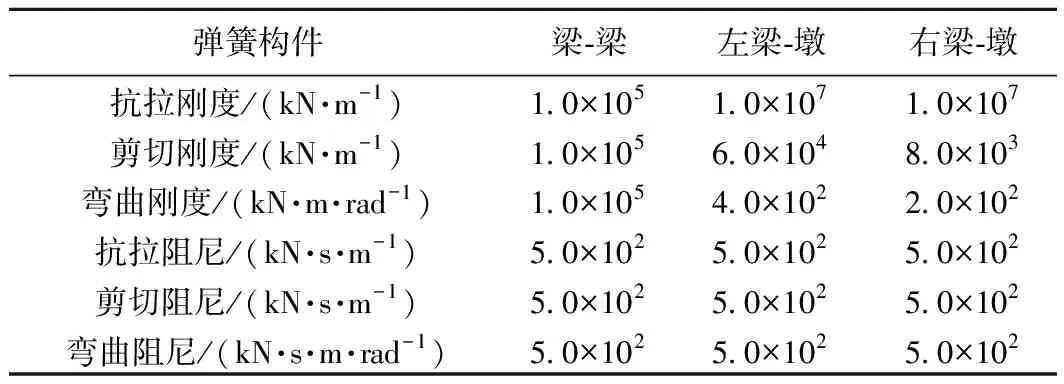
表2 接頭彈簧剛度和阻尼參數[6]

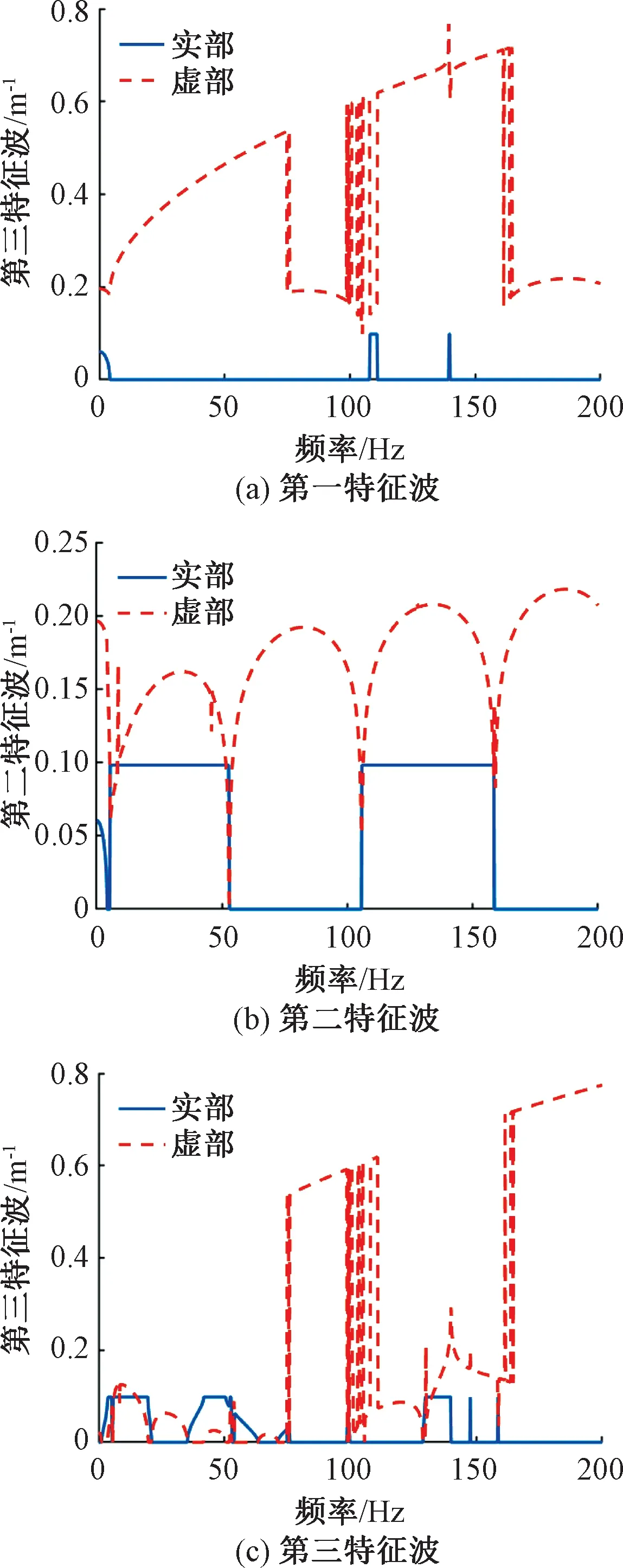
圖6 周期性橋梁結構的前三種特征波

由圖6可見，對于第一特征波，該周期性橋梁結構的通帶頻率范圍為0～4.3、107.8～111.0、139.4～140 Hz，同時其虛部隨頻率的增大而不斷增大，表明第一特征波的高頻段通帶衰減快；對于第二特征波，其通帶頻率范圍為0～4.3、5.2～53、105.6～158.6 Hz，同時其頻率虛部分布為兩端小中間大，表明那些衰減較慢傳播較遠的通帶頻率分布在通帶與禁帶界限處；對于第三特征波，其帶頻率范圍則有多個，即1.0～21.2、35.2～53.0、53.8～63.4、71.0～75.0、75.4～76.0、128.8～140.0 Hz。因此，若將32 m跨徑的高速鐵路周期性簡支梁橋作為隔振結構，第一、二、三特征波共有的通帶頻率是1.0～4.3、139.4～140 Hz，而其他頻段的波將會被阻礙。

3.3 周期性橋梁結構的響應及墩底動反力分析

利用本文的理論方法，可以計算周期性橋梁結構任意跨的動力響應及墩底產生的動反力。

以圖1的基本跨為基準，取其右側的第5、7、9跨進行橋墩墩底動反力的計算分析，該墩底的動作用力可作為場地的輸入激勵進行環境振動的分析。當輪軸荷載以V=300 km/h的速度移動時，橋墩墩底動反力力見圖7。 由圖7可見：第5、7、9跨墩底豎向反力、水平反力和反力矩時程曲線相互間隔0.77 s的時間差，且曲線幅值、走勢基本一致；三跨的橋墩墩底豎向反力幅值均為9.5×102kN，墩底水平反力幅值為3 kN，墩底彎矩幅值為12 kN·m，并且墩底水平力時程、彎矩時程曲線相對墩底豎向力時程變化劇烈；第5跨墩底豎向反力頻譜峰值集中在0～10 Hz，墩底水平反力頻譜峰值分布在5.7、33.7、67.2、104.3、131.5、168.0、198.3 Hz左右，墩底反力矩頻譜峰值分布在5.6、23.5、33.7、67.2 Hz左右，因此墩底豎向力頻譜主要分布在低頻段，而墩底水平反力、反力矩頻譜分布在中、低頻段。

準靜態輪軸荷載作用下，基本跨右側第5跨左端截面的豎向位移、彎矩及剪力的頻譜及時程曲線見圖8。由圖8可見，第5跨左端部豎向位移、彎矩及左梁接頭剪力頻譜峰值集中在0～10 Hz，即梁體跨中豎向位移、彎矩及梁端剪力頻譜主要分布在低頻段。同時結合圖6～圖8的計算結果可以看出，周期性橋梁結構的能帶特性主要還是應用于周期結構在隔振減振中的分析，而不能直接用來解釋移動荷載作用下周期性橋梁結構本身的動力響應頻譜分布特征。

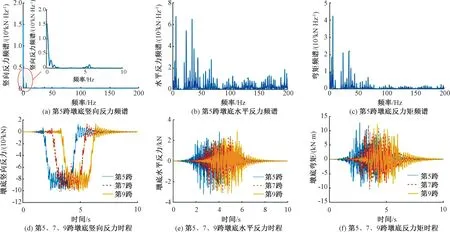
圖7 輪軸荷載作用下基本跨右側第5、7、9跨橋墩的墩底動反力(V=300 km/h)

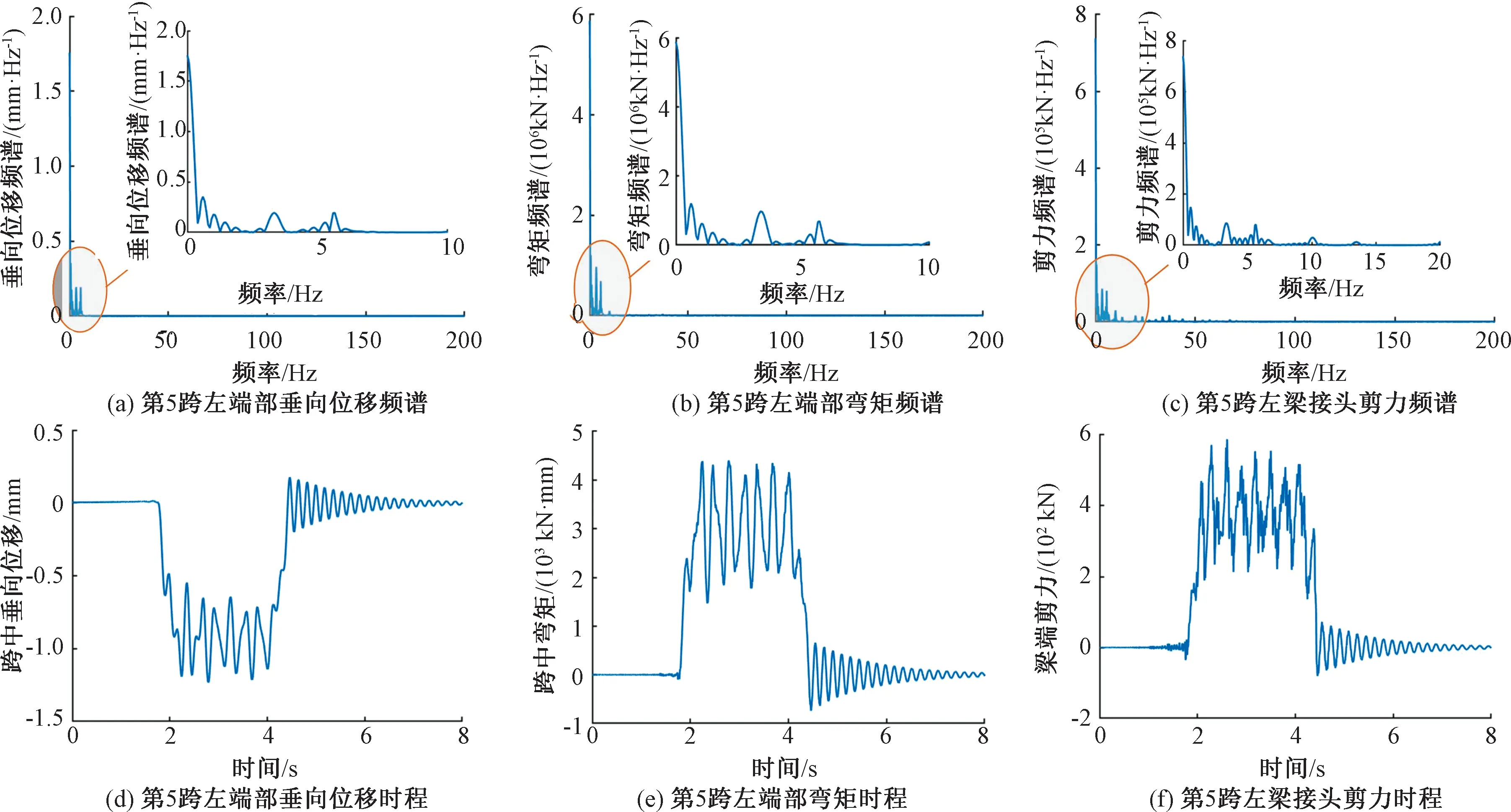
圖8 移動輪軸荷載作用下基本跨右側第5跨左端面的垂向位移、彎矩及剪力

為了能更加明確地分析激振頻率對結構振動響應的影響，本文除了考慮移動的準靜態輪軸荷載，還考慮了單一波長λ的軌道不平順。軌道不平順引起的激勵力P(x,t)=P0eiωpt，其中ωp=2πV/λ為軌道不平順引起的加載頻率(λ為軌道不平順的波長，V為列車運行速度)。以基本跨右側第5跨的左端面(即相應的跨中截面)為例，分別計算列車運行速度為300 km/h時，ωp=6.54、20、30 rad/s三種情況下橋梁結構的豎向位移頻譜圖和時程曲線，計算結果見圖9。

由圖9可見，外激勵力頻率對橋梁跨中位移的影響較大。與準靜態輪軸荷載作用下的動力響應進行對比可知，當不考慮軌道不平順時，位移曲線主要是由移動的輪軸荷載引起的，截面發生整體向下的位移，而考慮了軌道不平順后，截面位移出現了明顯的周期性特征，且隨激振頻率的增大而增大。

列車速度為300 km/h時，不同激振頻率下基本跨右側第5跨的移動輪軸荷載引起的墩底豎向力、水平反力以及反力矩的時程曲線見圖10。由圖10可見，墩底豎向力、水平力和力矩隨時間變化的曲線差異比較大；考慮了軌道不平順后，墩底作用力也出現了明顯的周期性特征，且隨激振頻率的增大而增大。因此，墩底動反力將會受到列車軸重準靜態激勵和軌道不平順激勵的雙重影響，當考慮軌道不平順隨機激勵時，這種影響將會更加明顯[18]。

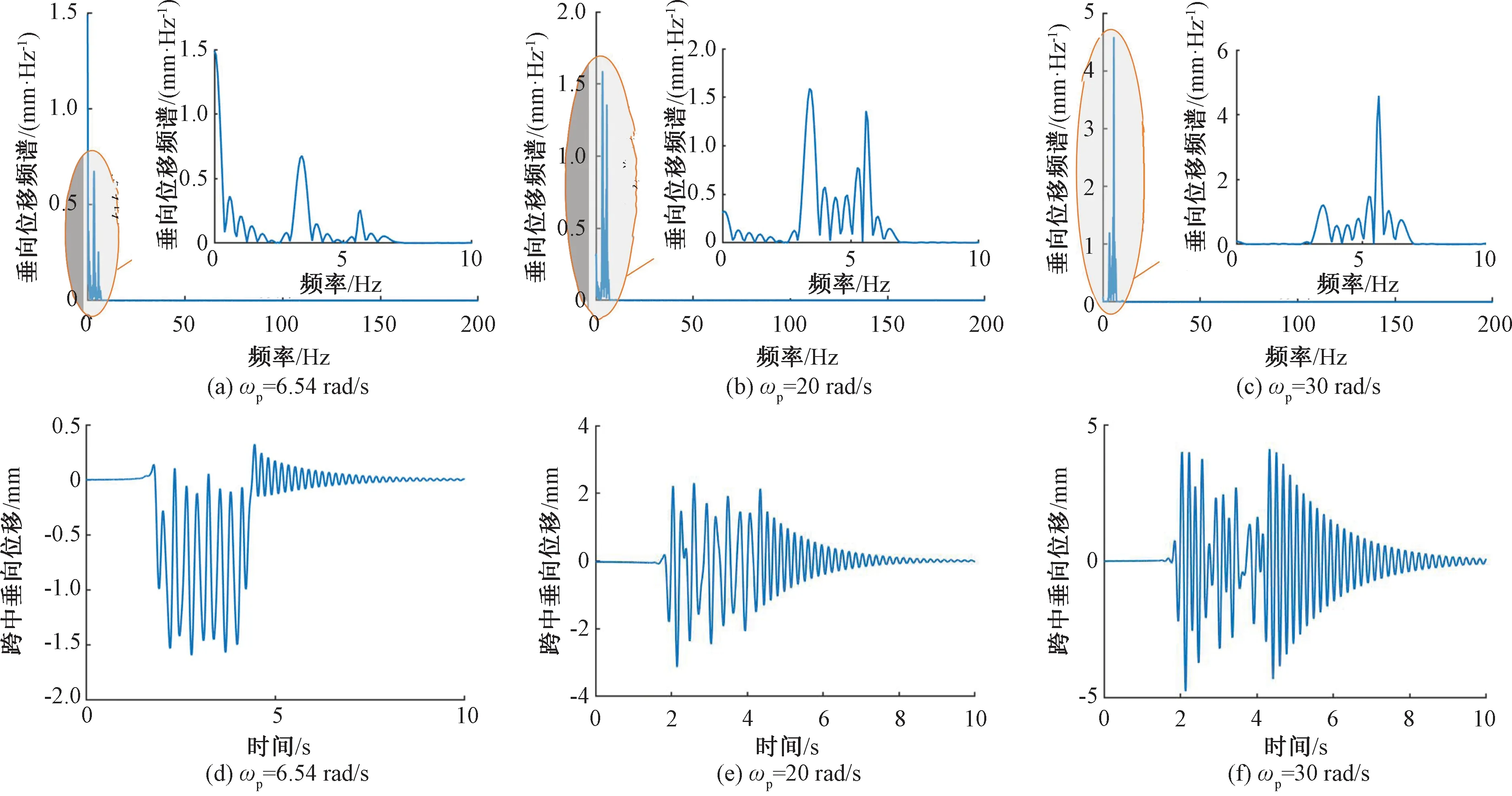
圖9 不同激振頻率下基本跨右側第5跨左端面的垂向位移頻譜和時程曲線(V=300 km/h)

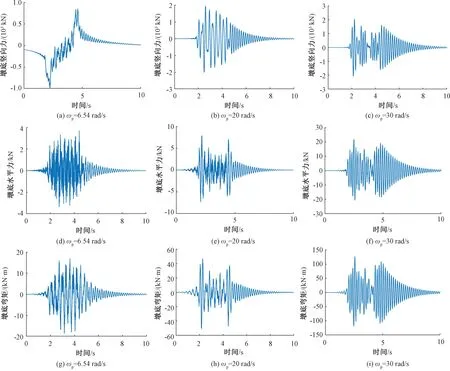
圖10 不同激振頻率下基本跨右側第5跨對應橋墩的墩底動反力(V=300 km/h)

4 結論

本文基于無限周期結構理論和頻域有限元法，建立了高速鐵路周期性橋梁結構的分析模型，提出了基本跨模型等效結點荷載矢量頻譜的計算方法，并通過既有文獻驗證了本文模型的正確性，主要結論如下：

(1)本文所提出的周期性橋梁結構頻域有限元模型及方法，不僅能夠直接從頻域內求解橋梁結構的動力響應以及墩底動反力，而且只需要建立基本跨的力學模型就可以求解橋梁結構任意跨的動態響應，計算方法高效且穩定，為環境振動研究領域中場地振動荷載源的求解提供了新的研究思路和計算方法。

(2)通過有限單元法求解了周期性橋梁結構的通帶和禁帶曲線，其第一特征波隨頻率增大其衰減也不斷增大，第二、三特征波在通帶與禁帶界限頻率處衰減較慢，且第一、二、三特征波在低頻和高頻段均有共有通帶頻率；其能帶特性可應用于周期結構的減振隔振中。

(3)由于軌道不平順的影響，橋梁結構截面位移和墩底動反力會出現明顯的周期性特征，且動力響應隨激振頻率的增大而增大。

(4)作為橋墩基礎—場地相互作用體系的外激勵力輸入時，不應該只考慮墩底的豎向作用力，還應將水平作用力和力矩作為輸入同時作用到承臺基礎的表面，同時還要考慮由軌道不平順引起的動態作用力。