直覺正態模糊數Choquet 積分算子及其決策應用

常娟，杜迎雪，劉衛鋒

（鄭州航空工業管理學院 數學學院，河南鄭州, 450046）

0 引言

多屬性決策方法（multi-attribute decision method,MADM）可用于解決工程、經濟和管理領域中的諸多問題。通常決策屬性指標體系應具有獨立性、完備性和代表性，但在實際問題中，屬性指標體系的獨立性常常難以滿足。例如，若用價格、性能和售后3個屬性指標選擇設備，一般來說，性能和售后好的設備價格高，即屬性間的權重不滿足可加性，若用加權算術平均算子（WA）對屬性信息集結，則屬性間的關聯可抵消各屬性的獨立貢獻[1]。因此，對屬性間存在關聯的MADM 問題的研究具有重要的理論和現實意義。1974 年，SUGENO[2]首次提出模糊測度的概念，MARICHAL[3]通過對模糊測度的研究，提出屬性間的關聯均可用模糊測度度量。而基于模糊測度的Choquet 積分[4-5]可以靈活地體現輸入變量間的相互關聯情況。因此，利用模糊測度和Choquet積分解決屬性間有關聯的MADM 問題，這一方法廣受關注。其中文獻[1,6-7]研究了在實數情況下屬性信息有關聯的MADM 方法，并用于解決實際問題。隨后研究者們相繼開展了對屬性間具有關聯性的模糊MADM 問題研究。其中，高巖等[8]利用Choquet 積分構造了非線性規劃模型，提出一種直覺模糊MADM 方 法；XU[9]和TAN 等[10-11]基 于Choquet 積分的直覺模糊數和區間直覺模糊數構造了關聯信息集成算子，并研究這些算子的性質，TAN 等[11]提出了基于Choquet 積分的逼近理想解排序（technique for order preferences by similarity to an ideal solution,TOPSIS）法，用于解決區間直覺模糊信息的MADM 問題；曲國華等[12]則結合模糊測度、Choquet 積分和Shapley 值，提出了改進的直覺模糊TOPSIS 法；王堅強 等[13]、萬樹平 等[14]研究基 于Choquet 積分的直覺三角模糊數的決策方法和集成算子，并分別給出了利用優化模型確定模糊測度的方法；陶長琪等[15]、周曉輝等[16]分別提出了基于Choquet 積分的直覺模糊數、區間直覺梯形模糊數信息集成算子，并給出了具體的決策方法。

考慮現實生活中大量隨機現象服從或近似服從正態分布，1996 年，YANG 等[17]定義了正態模糊數，指出正態模糊數在刻畫模糊信息時更接近人類思維，也更為準確[18]。在模糊MADM 問題中，可以借助數理統計的方法，給出正態模糊數形式的屬性信息。然而，單純用正態模糊數表示屬性值，則暗含決策者對這一信息是完全認可的，無法反映決策者對這一信息的信任程度和猶豫程度。而直覺模糊集的隸屬度、非隸屬度和猶豫度可細致刻畫決策者的支持、反對和中立三種態度。因此，結合直覺模糊集的思想，王堅強等[19]在正態模糊數基礎上增加了隸屬度和非隸屬度信息，并定義了直覺正態模糊數。目前，有關直覺正態模糊數的研究成果主要有：王堅強等[19-20]定義了直覺正態模糊數的運算、距離、得分函數和精確函數，提出直覺正態模糊數加權算術平均算子和誘導廣義有序加權平均算子；劉政敏等[21]則給出了不同于文獻[19]的直覺正態模糊數的運算法則，定義了直覺正態模糊數的期望值，并提出了準則間具有優先關系的直覺正態模糊數集成算子；常娟等[22]提出了權重由集結數據確定的直覺正態模糊數冪均算子；文獻[23-24]則定義了區間直覺正態模糊數的運算，并給出了區間直覺正態模糊數的一些集成算子，如有序加權幾何平均算子、連續有序加權幾何平均算子、誘導有序加權平均算子和誘導有序加權幾何平均算子。

上述關于直覺正態模糊數的集成算子均是基于屬性間相互獨立的情形下展開的討論，而在實際決策問題中，屬性間往往是相互關聯的。因此，研究屬性間的關聯性且屬性值為直覺正態模糊數的MADM 問題，具有重要的理論和實際意義。為此，在文獻[22]定義的直覺正態模糊數運算基礎上,利用模糊測度λ，將Choquet 積分用于直覺正態模糊數，構建直覺正態模糊數Choquet 積分平均（INFCA）算子和直覺正態模糊數Choquet 積分幾何（INFCG）算子，詳細探討其性質和特殊形式。此外，通過構建線性規劃模型，提出一種確定各屬性子集模糊測度λ的方法，進而給出基于直覺正態模糊Choquet 積分算子的MADM 方法。最后，通過實例驗證該方法的可行性和有效性。

1 相關概念

1.1 直覺正態模糊數

若正態 模糊數=(a,σ),則由定 義2，得E()=a,D()=。在實際問題中，可借助數理統計方法得到正態模糊數形式的屬性信息。例如，對某一實驗參數進行100 次觀測，經計算,樣本均值和標準差分別為0.669 0 和0.059 5，即a=0.669 0，=0.059 5，σ=0.084 1,則可用正態模糊數(0.669 0,0.084 1)表示該參數的觀測值。通過對正態模糊數添加隸屬度和非隸屬度，王堅強等[19]提出了直覺正態模糊數。

定義3[19]設(a,σ)∈,稱A=〈(a,σ),μA,νA〉為直覺正態模糊數，其隸屬函數和非隸屬函數分別為

1.2 模糊測度和Choquet 積分

定義7[2]設P(X)為有限集X的冪集,映射ψ:P(X)→[0,1]滿足條件：

（1）ψ(?)=0,ψ(X)=1;

（2）若X1，X2∈P(X)，X1?X2，則ψ(X1)≤ψ(X2)，稱ψ為X上的模糊測度。

為提高模糊測度計算的可行性，SUGENO 又提出了λ模糊測度。

定義8[2]給定λ∈(-1,∞),P(X)為有限集X的冪集，設映射gλ:P(X)→[0,1]滿足條件：

定義9[5]若f為定義在X={x1,x2,…,xn}上的非負函數，ψ為X上的模糊測度，則f關 于ψ的 離散Choquet 積分為

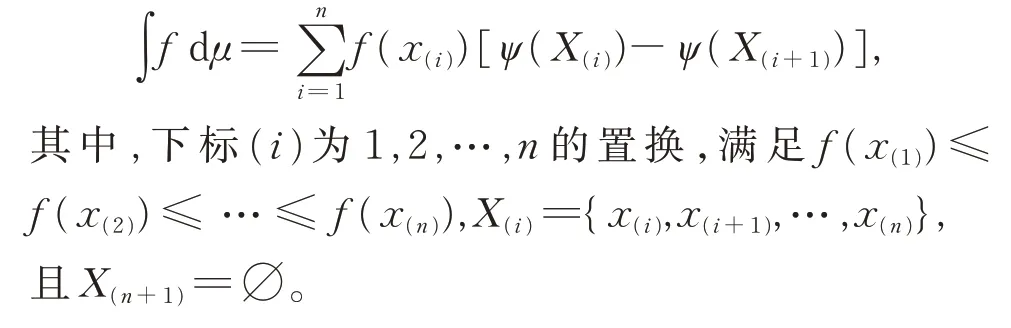
2 直覺正態模糊數Choquet 積分算子

基于模糊測度的Choquet 積分可以體現輸入信息間的關聯情況，鑒于此，為解決屬性間關聯的直覺正態模糊數MADM 問題，根據直覺正態模糊數的運算法則和Choquet 積分的定義，構造直覺正態模糊數Choquet 積分算子。

2.1 INFCA 算子

定義10設X={x1,x2,…,xn},定義在X上的直覺正 態模糊數組Ai=〈(ai,σi),μi,νi〉(i=1,2,…,n),ψ為X上的模 糊測度,Ai關 于ψ的離散Choquet 積分為

則稱INFCA 為直覺正態模糊數Choquet 積分平均算子，簡稱INFCA 算子。其中下標(i)為1,2,…,n的置換，滿 足A(1)≤A(2)≤…≤A(n),X(i)={x(i),x(i+1),…,x(n)},且X(n+1)=?。

定理1設定義在X上的直覺正態模糊數Ai=〈(ai,σi),μi,νi〉,i=1,2,…,n,ψ為X上的模糊測度，則INFCA(A1,A2,…,An)∈Ω,且INFCA(A1,A2,…,An)=

INFCA 算子的基本特點是：對直覺正態模糊數A1,A2,…,An按升序排列后進行加權關聯集成，將屬性子集的模糊測度差ψ(X(i))-ψ(X(i+1))作為集成時的位置權重，其與Ai無關。

INFCA 算子具有以下性質：

定 理 2設一組 正態模糊數Ai=〈(ai,σi),μi,νi〉,i=1,2,…,n,ψ為X上的模糊測度。其具有以下性質

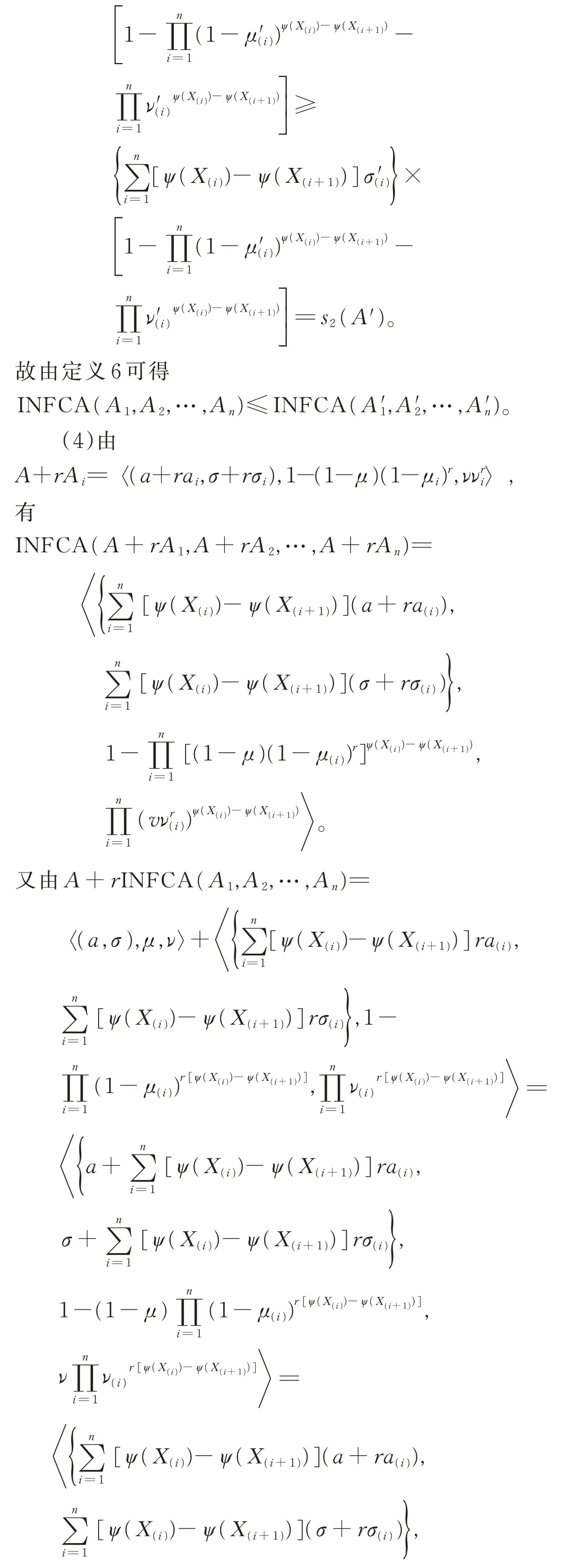
當X上的模糊測度ψ比較特殊時，INFCA 算子具有以下特殊形式：

（1）若對任意Y∈P(X),且Y≠?，有ψ(Y)=1,則INFCA(A1,A2,…,An)=max {Ai};

（2）若對任意Y∈P(X),且Y≠X，有ψ(Y)=0,則INFCA(A1,A2,…,An)=min {Ai};

（3）若對任 意Y∈P(X),有ψ(Y)=,則

此時，INFCA 算子即為直覺正態模糊數加權平均（INFWA）算子；

（4）設(w1,w2,…,wn)為INFOWA 算子的權重向量，Y∈P(X),且|Y|為Y 中的元素個數，若對任意Y∈P(X),ψ(Y)=,有

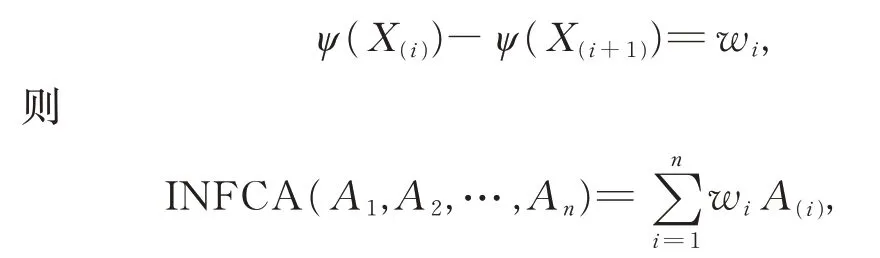
此時，INFCA 算子即為直覺正態模糊數有序加權平均（INFOWA）算子。

2.2 INFCG 算子

定義11設X={x1,x2,…,xn},定義在X上的直覺正 態模糊 數Ai=〈(ai,σi),μi,νi〉,i=1,2,…,n,ψ為X上的模 糊測度,Ai關 于ψ的離散Choquet 積分：

則稱INFCG 為直覺正態模糊數Choquet 積分幾何算子，簡稱INFCG 算子。其中下標(i)為1,2,…,n的置換，滿 足A(1)≤A(2)≤…≤A(n),X(i)={x(i),x(i+1),…,x(n)},且X(n+1)=?。

定理3設定義在X上的直覺正態模糊數Ai=〈(ai,σi),μi,νi〉,i=1,2,…,n,ψ為X上的模糊測度，則INFCG(A1,A2,…,An)∈Ω,且

同理，當X上的模糊測度ψ比較特殊時，INFCG算子具有以下特殊形式：

（1）若對任意Y∈P(X),且Y≠?，有ψ(Y)=1,則INFCG(A1,A2,…,An)=max {Ai};

（2）若對任意Y∈P(X),且Y≠X，有ψ(Y)=0,則INFCG(A1,A2,…,An)=min {Ai};

（3）若對任 意Y∈P(X),有ψ(Y)=,則

INFCG(A1,A2,…,An)=,

此時，INFCG 算子即為直覺正態模糊數加權幾何平均（INFWG）算子。

（4）設(w1,w2,…,wn)為INFOWG 算子的權重向量，Y∈P(X),且|Y|為Y 中元素的個數，若對任意Y∈P(X),ψ(Y)=,有

此時，INFCG 算子即為直覺正態模糊數有序加權幾何（INFOWG）算子。

3 決策應用

通過求解以上優化模型可得各屬性指標的λ模糊測度gi,i=1,2,…,n,再利用1+λ=確定參數λ的值，從而由定義8 可計算各屬性子集的λ模糊測度。

以下為基于INFCA（或INFCG）算子的直覺正態模糊數多屬性決策方法的具體步驟：

步驟1確定直覺正態模糊數決策矩陣(Aij)m×n。

步驟2規范化決策矩陣[19]。

步驟3計算各屬性指標的λ模糊測度,以確定各屬性子集的λ模糊測度。

步驟4利用INFCA（或INFCG）算子對各方案的屬性值進行集結，得到綜合屬性值。

步驟5利用定義6 對各方案的綜合屬性值從大到小進行排序，得到最優方案。

例1某制造公司在選擇供應商時，有4 個考核指標：供貨能力(u1)、交易能力(u2)、售后服務(u3)、企業實力(u4)，均為效益型指標，顯然，u1，u2，u4這3 個指標之間存在冗余關聯。設gλ(ui)=wi,i=1,2,3,4，表示各屬性指標的重要程度，經專家評定，滿足以下條件：0.1≤w1≤0.3,0.2≤w2≤0.4,0.3≤w3≤0.4,0.2 ≤w4≤0.4,0.3 ≤w1+w2≤0.4。現有4個供應商A1,A2,A3,A4,邀請多位相關領域專家，對各供應商進行實地考察，并對各指標的滿意度進行打分（10 分制）。經計算,供應商A1在供貨能力u1下所得平均分為3，標準差為0.282 8，由定義2,打分結果可用正態模糊數（3,0.4）表示，考慮專家對此結果的認可程度，對每位專家對正態模糊數（3,0.4）的接受程度再進行投票，若接受比例為0.7，不接受比例為0.2，則A1在u1下的指標值最終可通過直覺正態模糊數〈(3,0.4),0.7,0.2〉表示。類似地，可得到其他各項指標值，具體如表1 所示。最后篩選出最優供應商。

步驟1規范化決策矩陣，如表2 所示。

表1 直覺正態模糊數決策矩陣Table 1 Intuitive normal fuzzy numbers decision matrix

表2 直覺正態模糊數規范化決策矩陣Table 2 Intuitive normal fuzzy numbers normalized decision matrix

步驟2計算各屬性子集的模糊測度。

首先，通過線性規劃模型：

步驟3利用INFCA 算子對規范化后各方案的屬性值進行集結：

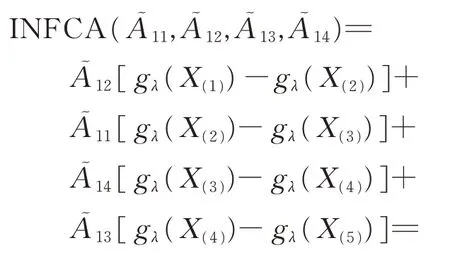
步驟4計算以上各方案綜合指標值的得分函數,分別得到0.317 0,0.523 2,0.375 9,0.726 8,則各供應商的排序結果為A4?A2?A3?A1,最優供應商為A4。

文獻[19，22]在不考慮屬性關聯情況下分別利用TOPSIS 法和冪均算子法（λ=2），得到的排序結果均為A4?A2?A1?A3，與本文方法得到的最優供應商為A4一致。表1 的數據也表明，A4的各項指標值占絕對優勢，決策結果是合理的，但A1,A3的排序發生了變化。可見，考慮指標間存在關聯性這一實際情況，確實會對排序結果產生影響。

4 結語

針對屬性間存在關聯性這一實際情況，筆者利用模糊測度和Choquet 積分，構造了INFCA 算子和INFCG 算子，經研究，這些算子具備較好的性質且具有一些特殊形式。在具體的多屬性決策問題中，如何確定各屬性子集的模糊測度，本文也給出了具體方法。實例結果表明，本文的決策方法是可行和有效的,符合直覺正態模糊信息的決策問題屬性間的關聯性，是對現有的直覺正態模糊理論成果的補充和完善。