稀疏數據情況下小橢圓軌道目標再入預報方法

張煒，崔文，張育衛，劉興，李菊清

(西安衛星測控中心，西安710600)

1 引言

大氣阻力是即將再入空間目標所受的最主要非保守攝動力，精確的空間目標面質比及合理的大氣阻力特性建模是準確計算大氣阻力加速度、預報再入時間的關鍵。大氣阻力系數與空間目標外形、表面材料、大氣組成及溫度等密切相關，同一個目標的大氣阻力系數在不同軌道高度、不同太陽活動水平等情況下會有較大差異[1]。通常，空間目標的準確外形、質量、姿態和表面材料等都是未知的，分別確定大氣阻力系數、迎風面積和質量難度很大，因此引入彈道系數B進行統一處理[2]。彈道系數的定義為:

式中，CD為大氣阻力系數；A為迎風面積；m為質量。

在大氣阻力的影響下，空間目標的軌道不斷衰減，軌道形狀越來越圓，最終墜入稠密大氣層。按初始遠地點高度Ha_ini(本文的 “初始”指空間目標再入前10天)對再入目標軌道進行分類:

(1)近圓軌道:Ha_ini＜500km

(2)小橢圓軌道:500km≤Ha_ini＜5000km

(3)大橢圓軌道:Ha_ini≥5000km

依此統計，2012—2018年非受控再入的大型空間目標數量，結果如圖1所示。可以看出，每年再入的大型空間目標中小橢圓軌道目標不在少數，近7年平均占1/6以上，2018年更是超過40%。

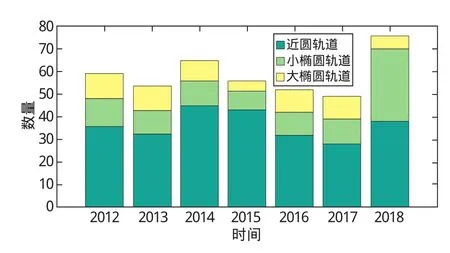
圖1 2012年至2018年非受控再入的大型空間目標數量Fig.1 Number of large uncontrolled reentry objects from 2012 to 2018

再入預報的主要難點在于軌道確定和大氣阻力建模[3]，一般在足夠測量數據的基礎上確定精確軌道并解算彈道系數，但是只有少數國家和組織具有獲取再入目標測量數據的能力。即使可以，相鄰圈次的間隔可能太長導致難以聯合使用確定精密軌道，容易出現定軌殘差太大、不收斂等問題，這也是本文 “稀疏數據”這一基本背景。“地球重力場和海洋環流探測衛星”(GOCE)再入前20天起，布設于德國Wachtberg的跟蹤及成像雷達 (TIRA)共獲取12圈次測量數據，不同數據組合的定軌結果明顯差異[4]，在沒有基準星歷的情況下難以選優。目前大部分再入預報研究只能依靠美國戰略司令部于Space-track網站公開發布的兩行根數 (TLE)，基于TLE的再入預報方法研究主要聚焦于TLE的預處理[5，6]，或利用TLE解算彈道系數、太陽光壓系數、狀態矢量等[7-11]。幾乎所有的研究均假設再入目標的彈道系數是一個常數，顯然這是不夠準確的，尤其對于橢圓軌道再入目標而言，容易忽略彈道系數變化帶來的問題。

相較于近圓軌道目標，小橢圓軌道目標的再入預報難度更大。主要原因是小橢圓軌道目標再入過程中幾乎每圈都要穿過整個稠密大氣層，高度變化導致同一軌道周期內彈道系數變化明顯。實際應用中發現，若采用整個數據弧段內解算單個彈道系數的策略，各測量元素的殘差可能較大，難以判斷軌道確定結果的準確性，而采用分段解算多個彈道系數的策略，雖然可以獲得更加精確的目標軌道，但是進行再入預報時彈道系數的初值難以選擇。

本文針對稀疏數據情況和小橢圓軌道的特點，提出使用平均彈道系數進行再入預報。利用半數值法計算平均彈道系數、數值法進行短弧數據軌道確定和軌道外推，并使用實測數據進行效果驗證。結果表明，本文提出的方法可有效避免稀疏數據情況下小橢圓軌道目標軌道確定收斂難或殘差過大、再入預報時彈道系數難確定等問題，預報精度達到與近圓軌道目標同等水平。

2 方法

本文針對稀疏數據情況和小橢圓軌道的特點，提出半數值法和數值法相結合預報再入時刻。 使用經典軌道根數σ(a，e，i，Ω，ω，M) 描述再入目標軌道， (a，e，i，Ω，ω，M) 分別為半長軸、 偏心率、傾角、升交點赤經和平近點角。

2.1 軌道確定

稀疏數據情況是指測量數據圈次太少，例如24h內僅有1～2圈測量數據，多圈數據聯合確定軌道時容易出現殘差太大、不收斂等問題。本文使用短弧數據定軌方法對單圈數據分別確定軌道，考慮的攝動項包括:地球非球形引力、大氣阻力和日月引力。短弧數據定軌的問題主要在于軌道外推時誤差容易迅速發散，但是本文僅需數據弧段內的6個參數，可有效避免不收斂和誤差發散等問題。軌道結果精度主要受限于測量精度，與基于大量測量數據的精密軌道相比，短弧數據軌道位置誤差一般為幾百米，且主要集中在對再入預報影響最小的沿跡方向[12]。

基于單圈測量數據的軌道確定結果為密切根數 (σ1，σ2，…，σN) ， 本文還用到對應的平根數。去除密切根數中的短周期項即可得到平根數，即:

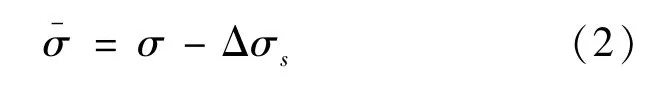
式中，為平根數；σ為密切根數；Δσs為短周期項。平根數的計算方法及短周期項的詳細討論可參考文獻 [13]—文獻 [16]。沒有可用測量數據的情況下可以使用TLE根數作為偽測量數據，使用SGP4/SDP4模型解析TLE歷元時刻的位置速度，并轉換成軌道根數。

2.2 平均彈道系數

如何計算再入目標的彈道系數是許多再入預報研究的焦點。在大多數研究中再入目標的彈道系數被視為常數，采用將彈道系數作為待估參數的策略，在軌道確定時與狀態參量(r，r)一同求解，再基于彈道系數和狀態參量的解算結果進行再入預報。但是這種方法對小橢圓軌道目標并不完全適用，由于空間目標的彈道系數 (主要是大氣阻力系數)隨高度變化，如果整個數據弧段內解算單個彈道系數，各測量元素的殘差可能較大導致難以判斷軌道確定結果的準確性；如果分段解算多個彈道系數，進行再入預報時難以選擇彈道系數的初值。為避免這些問題，提出基于空間目標軌道周期內的彈道系數平均值進行再入預報。平均彈道系數反映了一軌道周期內大氣阻力的平均效果，定義為:

式中，ρ為大氣密度值。為書寫方便，下文統一寫為B。

大氣阻力僅有長期作用效果，因此進行彈道系數擬合時可以采用開普勒平根數作為根數系統，并使用半數值法進行軌道積分，積分考慮的攝動項包括地球非球形J2項、J3項、大氣阻力。使用半數值法時高階攝動力建模較為困難和復雜，且精度改進效果不明顯[17]。積分模型如下[18]:

式中，v為再入目標相對大氣的運動速度；f為真近點角；ωE為地球運動速率；μ為地球引力常數；rE為地球半徑；n為平運動；p為軌道半通徑；J2、J3分別為地球引力場二階、三階帶諧系數。本文使用MSIS-90模型計算大氣密度。由于根數系統不包含短周期項，因此積分步長可以使用軌道周期的整數倍。

假設已有空間目標連續N組軌道平根數(，)，平均彈道系數的計算過程如下:

(1)以及初始平均彈道系數B0為初值，一軌道周期為步長對公式 (4)進行反向積分。反向積分的目的是防止彈道系數初值偏差太大導致積分過程 “鉆地”。

(2)若積分時刻與歷元之差小于半周期，則計算當前時間半長軸計算值與實測值之差Δak及半長軸對彈道系數的偏導數根據公式 (5)計算:

(3)第1條根數計算結束后，使用公式 (6)計算彈道系數修正值:

(4)若ΔB小于收斂閾值，則計算結束，否則對彈道系數進行修正:Bj+1=Bj+ΔB，返回 (1)重新計算。

2.3 再入時間預報

以第N圈數據確定的軌道密切根數σN及彈道系數計算結果B為初值，用數值積分的方法進行軌道外推，直到再入目標的平均軌道高度低于80km，積分結束時間后約5min即為空間目標的再入時間。數值積分使用10階定步長KSG積分器，用到的攝動力及其模型如表1所示。

表1 再入預報使用的攝動力及模型Table 1 Dynamical and geometrical models employed in the reentry prediction

由于不同大氣模型計算得到的大氣密度值存在差異[19]，因此彈道系數擬合和再入預報時應使用同一大氣模型，本文均使用MSIS-90模型。

3 數據與結果

使用誤差百分比δ評估再入預報的精度，誤差百分比δ用下式計算:

式中，treal為空間目標的實際再入時間；tpred為預報的再入時間；t0為進行再入預報所用初軌的歷元。從公開資料看，近圓軌道空間目標的再入預報誤差基本在10%～20%之間，部分預報結果誤差甚至可能超過30%，這主要取決于再入過程中再入目標姿態和大氣環境的變化[20，21]。

選擇美國銥星52(NORAD編號為25169)作為算例目標進行驗證，其初始近地點高度約為154km、遠地點高度約為608km。根據Space-track網站發布的信息，銥星52的再入時間為2018-11-05 21∶20(UTC)，與本文最后一次預報結果基本一致，因此treal取為 2018-11-05 21∶20(UTC)。從2018年10月27日起，選擇間隔10h以上的連續3圈測量數據進行再入預報，銥星52的平均彈道系數及再入時間預報結果如表2、圖2所示。

為了更直觀地理解平均彈道系數的計算效果，預報時大氣環境參數使用的均為實際觀測值，期間大氣環境平靜，大氣模型誤差對平均彈道系數結果影響較小。從計算結果看，銥星52的彈道系數在0.0251～0.0256m2/kg之間變化，均值為0.02548m2/kg，上下浮動1%左右，遠小于大氣阻力系數軌道周期內約10%的變化幅度，驗證了平均彈道系數計算方法的準確性和有效性。10次再入時間預報結果中的最大誤差僅為3.25%，其中8次計算的誤差小于1%。

按照本文提出的再入預報方法，選擇TLE作為數據源對2017年再入的11個小橢圓軌道目標進行再入預報。再入預報時將5天內每天1組TLE組成根數序列，并將根數序列視為再入目標的實測軌道值。再入前10天起每天進行一次預報，預報時大氣環境參數使用預報值，具有不確定性，各目標10次預報中的實際最大預報誤差如圖3所示。可以看出，11個目標中9個目標的再入預報誤差小于15%，預報誤差與初始偏心率 (或初始遠地點高度)無明顯相關性，說明本文方法具有較好的適用性。另外兩個分別為35.6% (目標NORAD編號為41726)和42.5%(目標NORAD編號為09980)，由于TLE使用前未作異常值篩選，分析認為異常TLE是造成這兩個目標最大誤差偏大的主要原因。從圖3也可以看到，使用TLE進行再入預報也能獲得較高的預報精度。

表2 銥星52再入預報結果Table 2 Reentry prediction results of Iridium-52

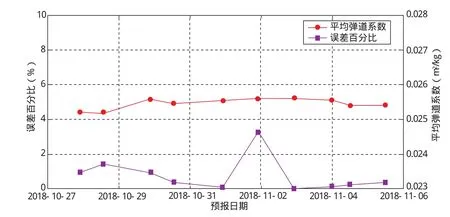
圖2 銥星52的再入預報誤差百分比及彈道系數Fig.2 Relative error and mean ballistic coefficient of Iridium-52

圖3 2017年再入的11個小橢圓軌道目標的最大預報誤差Fig.3 Maximum relative error of 11 reentry objects with low-eccentricity orbits in 2017

4 結論

由于大氣阻力系數隨高度變化，小橢圓軌道目標的再入預報比近圓軌道目標難度更大。本文針對稀疏數據情況和小橢圓軌道的特點，提出使用平均彈道系數進行再入預報，并使用再入目標的實測數據進行驗證。結果表明，基于平均彈道系數進行小橢圓軌道目標再入預報，可有效降低再入預報誤差，預報精度達到與近圓軌道目標同等水平。