隕石音爆研究思路及彈道靶試驗

王宗浩，黨雷寧，柳森

(中國空氣動力研究與發展中心超高速所，綿陽621000)

1 引言

小行星極高速進入稠密大氣過程中會產生較大范圍的沖擊波，可能造成地面建筑物損毀和人員傷亡。沖擊波產生的原因有兩種，一是隕石在空中爆炸，二是隕石極高速飛行產生的強激波，即音爆。隕石音爆的形成機理與超聲速飛機類似，都是激波穿過大氣傳播到地面造成局部短時超壓，不同的是隕石飛行馬赫數極高，形成的激波形狀類似圓柱形，且激波強度更大。

人們認識音爆問題始于第二次世界大戰末期對超音速射彈飛行產生的激波的研究，但直到1947年美國X-1飛機超越音速，音爆才開始引起學者的廣泛關注。經過數十年的試驗和理論研究，目前從現象和規律層面對音爆都已經有比較全面的掌握，包括在非均勻大氣中的傳播、飛機非定常飛行時的效應等。但針對隕石在大氣層內極高速 (通常為數千米/秒至數十千米/秒)飛行所導致的音爆現象，國內外研究報道較少。

本文總結了當前音爆研究的主要理論、計算方法和試驗技術，從隕石音爆問題出發，分析了其中的科學問題和現有研究手段的不足，提出了一種仿真和試驗結合的隕石音爆問題研究策略，并結合彈道靶試驗開展了隕石音爆的初步測量和仿真對比。

2 音爆研究方法

2.1 經典音爆理論

考慮平面波擾動下的介質微元，由波動方程可得到擾動波的傳播速度:

當擾動波為小振幅聲波時，由于聲壓很低，聲波的傳播速度可近似為U?≈c0，但是對于音爆這種有限振幅的波動，當地聲速和振動速度均為不可忽略的非線性項，因此波形在傳播過程中會產生畸變，如圖1所示。圖中，A點為正峰壓，其傳播速度快于c0，隨時間推移逐漸超前到波的頭部；B點為負峰壓，其傳播速度慢于c0，隨時間推移逐漸落后到波的尾部；最終形成N形波。

經典的音爆傳播模型，針對于亞聲速和一般超聲速均勻流動，采用小擾動假設將基本方程線性化 (但是對于跨聲速和高超聲速流動，基本方程簡化后仍然是非線性的)，得到的表征擾動傳播方向的特性線是一系列角度等于馬赫角的平行線。而如前所述，實際超聲速擾動波的傳播速度是受到當地聲壓和擾動速度變化影響的，特征線存在相交，擾動相互疊加并形成激波。因此，直接采用線性簡化方法并不能很好地描述音爆形成和傳播機制。1952年，Whitham提出一個修正的小擾動線化理論[1]，確定了特征線疊加所形成的激波線位置，并給出了遠場擾動速度計算式的形式:

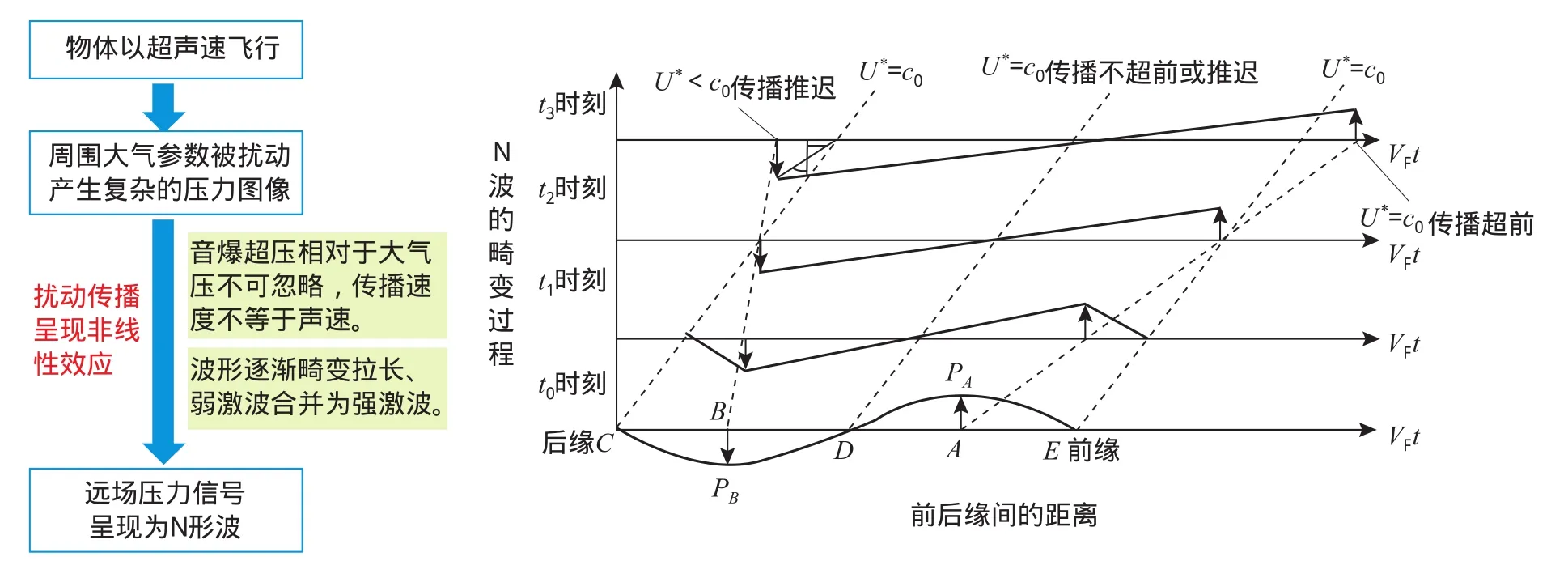
圖1 平面行波聲壓波形的畸變過程Fig.1 Distortion process of sound pressure waveform of traveling plane wave

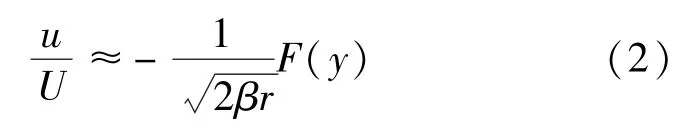
式中，F(y)為Whitham方程

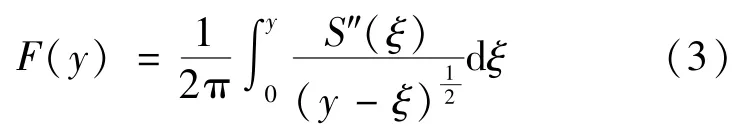
1963年，Friedman，Kane和Sigalla首先提出了基于射線跟蹤法的音爆計算模型[2]，該模型可以更好地描述大氣高度變化及層流風的影響，并且可以計算非定常飛行效應。但是Friedman等人的模型存在計算射線發展的側向分量的錯誤。之后Hayes等人建立的ARAP模型解決了這一問題[3]。同一時期Thomas也研究了一套與Hayes相似的計算模型[4]，不同于Hayes采用估算一組封閉積分，Thomas通過對一組穿越大氣層的射線路徑進行數值擬合實現射線跟蹤，并引入了 “波形參數”法實現了對傳播過程的波形連續演化分析。波形參數法以其計算量小、精確度高的特點得到廣泛應用。20世紀70年代，Carlson研究建立了一種簡化音爆預測方法 (Simplified Sonic Boom Prediction，SSBP)，其以大量計算機計算結果為基礎數據，并采用 “形狀因子”表征不同類型的飛機，通過擬合求解音爆源強度[5]。

其它方面，試驗測量表明大氣風場和湍流對音爆的遠場波形有明顯影響，激波附近的波形會發生扭曲，峰值的上升時間會變長，采用射線理論求解連續波與湍流的相互作用非常困難。Crow通過在薄激波區域構建一種以與激波距離為參數的拋物面散射方程來描述激波的扭曲[6]。而對于上升時間的預測，Plotki和George研發了Burgers方程以描述與湍流有關的耗散問題[7]，Pierce研發了一種基于波前折疊的理論[8]，盡管這些方法并不完善，但至今仍然是僅有的可用于定量分析的模型。

2.2 現代音爆計算方法和相關程序

由于音爆研究空間尺度較大，當前主流的方法是將計算域劃分為近中場和遠場兩個區域，如圖2所示。近中場一般采用可壓縮流動的CFD代碼計算。遠場計算以近中場CFD結果為輸入條件外推到地表，其中涉及到壓力波在分層大氣的傳輸，風場和湍流、溫濕度等的影響。遠場的計算結果是評估音爆對地面人和建筑物影響的依據，是音爆數值計算的關鍵技術之一。

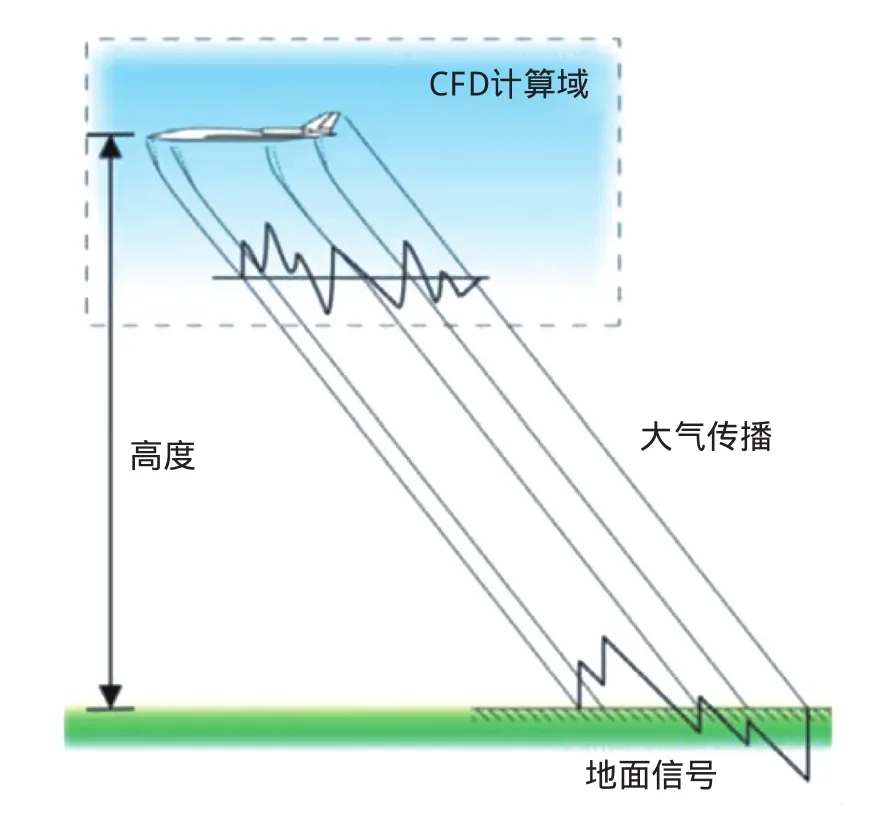
圖2 音爆傳播問題分區計算策略Fig.2 Zoning computation strategy for sonic boom

遠場計算方法有多種，例如建立在幾何聲學基礎上的F函數法和波形參數法、求解全速度勢方程法、求解Burger方程法等，有的研究者甚至通過求解Euler方程來計算音爆的遠場特性。

20世紀80年代以后，隨著計算機技術的進步，CFD仿真逐漸取代了F函數求解近場源參數， 美國先后發展了 Cart3D[9，10]、 PCBoom[11]、sBoom[12]等多個音爆計算和優化軟件，并通過多型飛機的實測數據對軟件計算模型進行標定和驗證。

2.3 音爆試驗研究進展

音爆試驗研究以飛行試驗為主，美國自20世紀50年代起至今在超音速飛機研制需求推動下開展了系統性的試驗研究工作。另外，以彈道靶為代表的特種超高速地面試驗設備在音爆研究方面也發揮了獨特作用。

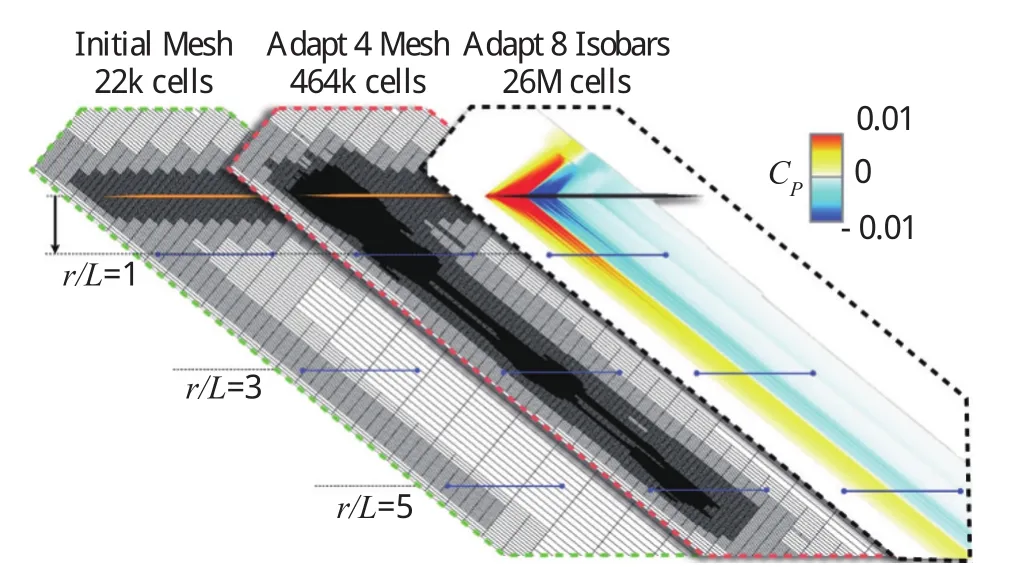
圖3 Cart3D軟件AXIE模型音爆計算網格優化結果Fig.3 Sonic boom computation grid optimization by Cart3D AXIE model

音爆的飛行試驗采用地面布設的麥克風測量超音速飛機以不同高度、飛行參數和氣候條件下掠過時的信號，通過對比分析理解和研究音爆的特性，校核和改進預測方法。1950—2000年，美國針對飛機音爆先后開展了10余項試驗項目。早期的試驗研究主要驗證Whitham理論關于N形波幅值和長度與飛機幾何尺寸間的關系。結果表明僅以飛機體積計算的飛機音爆最高可低于試驗值40%，且隨當地環境條件的變化，音爆從高空到地面的幅值會放大。這促進了機翼升力以及壓力梯度對音爆影響的研究以及對音爆理論的修正。

美國國家航空航天局蘭利研究中心 (NASALangley)從20世紀60年代開始探索音爆的風洞試驗技術。受限于風洞尺寸，音爆試驗的飛機模型需要縮比到很小，加工制造的難度極大。另外，非均勻和非穩態的風洞來流、模型和探針的振動、邊界層效應以及近場壓力信號的復雜性等都給風洞試驗的設計和開展造成困難。盡管開展音爆地面試驗模擬的難度很大，一些特殊的模擬設備，如彈道靶，依然可以在音爆問題試驗研究中發揮作用。彈道靶采用火藥或高壓氣體驅動的發射器加速模型到一定速度進入密閉的測試段自由飛行，由于沒有支架和背景噪聲干擾，試驗結果可以為CFD方法驗證提供很好的對比。

2000年，為驗證一種新的低阻低音爆的鈍前緣飛行器外形概念 (ABLE)，美國國家航空航天局-艾姆斯研究中心 (NASA-Ames)在彈道靶(HFFAF)上成功開展了自由飛模型的音爆測量試驗[13]。選用的發射器口徑為44mm，模型長度76.2mm，將壓力傳感器安裝在測試段壁面，測量面與壁面平齊。圖4為馬赫數2，雷諾數3×106，對應模擬高度15km條件下測量得到的模型流場紋影圖像和近場壓力信號。

3 隕石音爆問題研究思路

3.1 隕石音爆研究中的科學問題

研究隕石音爆的重要意義在于準確預測其對地面的危害，為隕石事件的預警和防減災提供指導，因此需要建立科學的方法預測給定彈道條件下的隕石音爆地面強度和影響范圍。總體研究思路可以借鑒飛機音爆的研究方法，但其中面臨的新問題需要關注。

圖4 HFFAF彈道靶自由飛模型的紋影圖像和音爆波測量結果Fig.4 Schlieren image and sonic boom measuring result of HEFAF ballistic range free flight model

一是需要發展極高速條件下隕石近場流場和激波強度的計算模擬方法。隕石進入過程存在復雜的超高速空氣動力學問題，如極高速進入條件下的氣動力與軌跡、氣動加熱與燒蝕、高溫氣體效應等，而這些均屬于當前空氣動力學的難題。只有解決這些基礎氣動問題，建立相應的物理模型才可能較準確預測隕石近場激波結構和強度，從而獲得隕石音爆地面影響分析的輸入條件。

二是需要完善強激波大氣傳播理論。由于隕石飛行馬赫數極高，其激波傳播過程具有強非線性特征，基于小擾動假設的線性簡化工程模型不再適用，需對現有方法和模型進行完善和驗證。

三是獲取真實試驗數據面臨挑戰。針對飛機音爆的飛行試驗研究容易實施，而隕石事件的稀少性和隨機性給實地測量帶來了困難。基于地面超高速試驗設備發展隕石音爆測量技術開展地面模擬試驗，可能是獲取基礎研究數據的唯一有效途徑。

3.2 隕石音爆研究思路

結合當前理論基礎和試驗條件，采取計算與試驗相結合的策略開展隕石音爆強度和傳播規律研究是可行的。理論與計算方法方面，主要參考飛機音爆研究方法，將研究速度拓展到10km/s以上。試驗方面，主要依托彈道靶設備開展2～7km/s速度范圍的對比驗證。

研究思路如圖5所示。考慮高溫燒蝕和真實氣體效應條件下的化學反應，建立近、中場壓力分布高精度數值計算模型，經彈道靶試驗驗證和改進后用于獲得隕石飛行中的近、中場壓力分布。以此為輸入，進一步將結果外推至遠場，需考慮大氣密度梯度、風場和湍流、溫濕度等的影響，可以嘗試在現有方法，如求解Burgers方程等的基礎上改進完善。

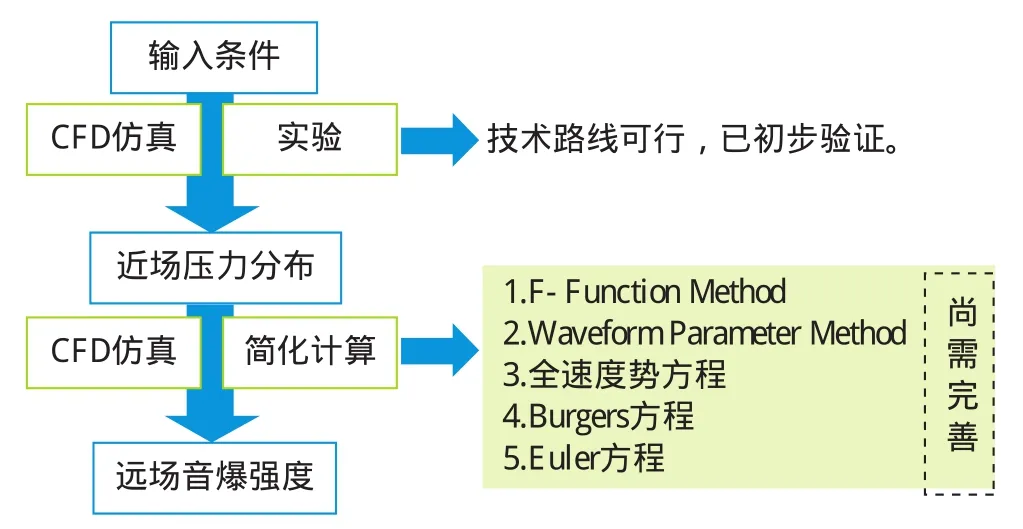
圖5 隕石音爆研究方法Fig.5 Meteorite sonic boom research method

4 隕石音爆的彈道靶模擬試驗

4.1 彈道靶隕石音爆試驗方法

彈道靶是一種超高速模擬設備，其系統組成如圖6所示。發射器系統采用二級輕氣炮加速模型，最高速度可達8km/s；靶室系統為飛行測試段，可模擬大氣環境；測試系統包含速度測量、流場顯示、壓力測量等儀器設備。

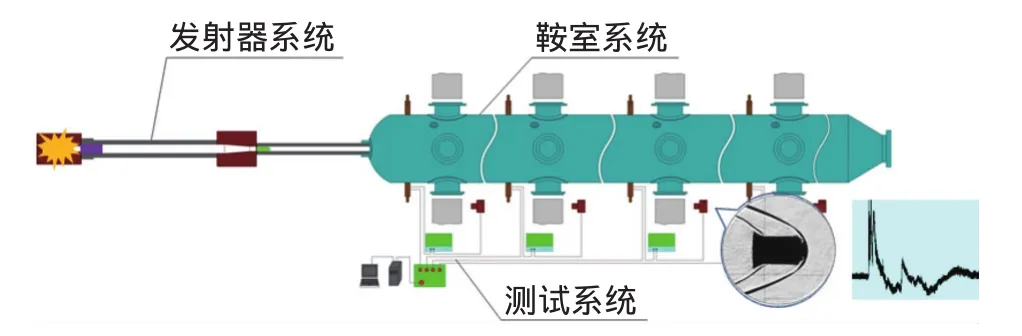
圖6 彈道靶原理圖Fig.6 Schematic diagram of ballistic range

采用彈道靶模擬隕石超高速飛行過程，可獲得中、近場壓力分布數據為計算方法研究提供校驗數據。具體試驗方法為:首先，設計適用于彈道靶設備的隕石模型，設計合理的壓力測量方案，選擇高精度的壓力傳感器搭建測量系統，如圖7所示，布置高分辨率陰/紋影成像系統用于記錄模型飛行姿態和流場結構；其次，在2～7km/s范圍內選取典型狀態開展試驗測量，獲得中、近場壓力分布數據和流場顯示結果；最后，用試驗數據核驗計算方法。

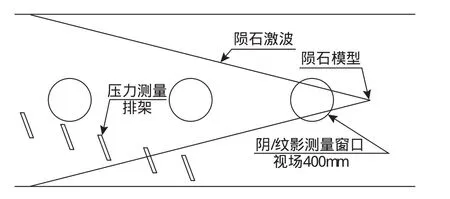
圖7 彈道靶音爆測試布置示意Fig.7 Ballistic range sonic test layout

4.2 試驗狀態和結果

近期，為驗證彈道靶開展隕石音爆研究的技術可行性，在中國空氣動力研究與發展中心200m自由飛彈道靶上開展了一次測量試驗，如圖8所示。不同的隕石在材料成分、孔隙率、形狀和尺寸等方面均存在差異，其中材料和孔隙率極大影響氣動燒蝕乃至解體的程度，而流場結構和音爆強度主要決定于形狀、尺寸和進入速度等因素。考慮到隕石一般為橢球形，結合彈道靶設備發射能力和模型飛行穩定性要求，選擇長徑比較小的球頭柱加尾裙的旋成體為試驗對象，其球頭半徑為30mm，總長度為50mm。雖然真實隕石表面的坑洞或孔隙會導致復雜的近壁面流場，簡單模型無法完全模擬，但決定峰值超壓的脫體激波強度與采用簡化模型的結果是相近的，用于驗證測量技術和計算方法是有意義的。試驗中，模型飛行速度約3.5km/s，測試段為常壓環境，在模型飛行軸線正下方112cm處前后間隔10cm布置了兩支PCB113B28傳感器 (采樣頻率500kHz)，模型尺寸及傳感器布置如圖9所示。

彈道靶隕石音爆測量試驗獲得的PCB傳感器時域信號如圖10所示，其中第一個N形波為隕石模型飛行激波首次掃掠測量面時的超壓信號，其峰值超壓約35kPa。

4.3 CFD計算對比

進一步，針對試驗條件采用二維軸對稱網格、理想氣體和K-ω SST湍流模型開展了流場仿真，得到了模型近場不同距離處的音爆波形及峰值超壓。結果顯示模型近場由中心向外的激波超壓呈快速衰減趨勢，計算得到的音爆波形與試驗測量結果相似，但峰值超壓高于實測結果。要進一步提高計算方法的預測精度，則材料的氣動加熱和燒蝕損傷、真實氣體的化學非平衡流動效應不可忽略。

圖8 200m自由飛彈道靶Fig.8 200m free flight ballistic range

圖9 彈道靶隕石音爆測量傳感器現場布置情況Fig.9 Ballistic range meteorite sonic boom measurement sensor site layout

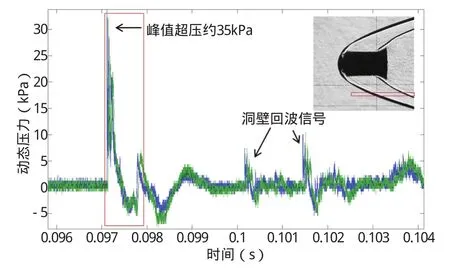
圖10 彈道靶隕石音爆測量試驗獲得的PCB傳感器時域信號和流場陰影圖像Fig.10 PCB sensor time domain signal and flow field shadow resulting from ballistic range meteorite sonic boom measurement test

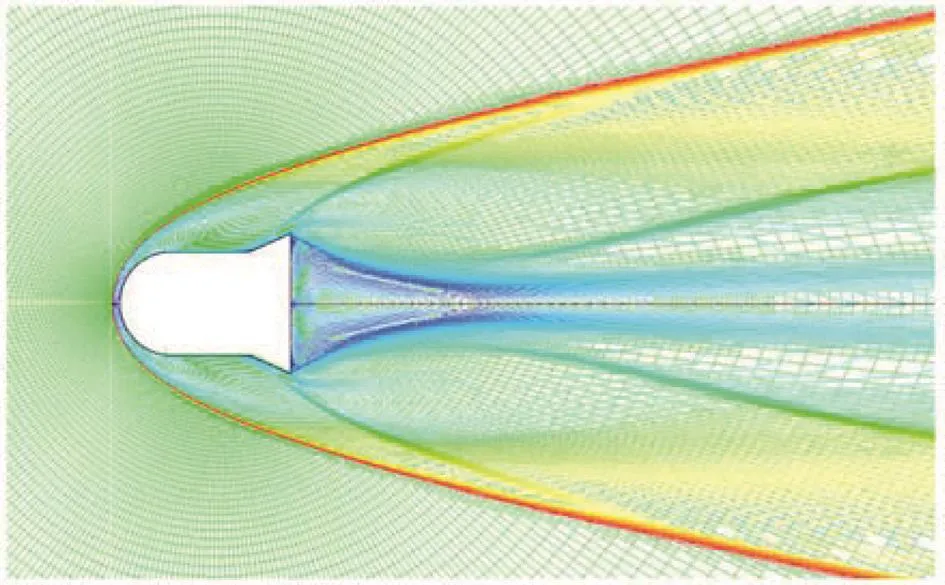
圖11 CFD計算網格和流場馬赫數云圖Fig.11 CFD computational grid and flow field Mach number cloud image

5 結論

本文梳理了國內外在音爆預測理論、音爆試驗模擬方法等方面的研究進展，從隕石音爆問題出發，分析了其中的科學問題和現有研究手段的不足，提出了一種仿真和試驗結合的隕石音爆問題研究策略，并介紹了在彈道靶上開展隕石音爆模擬試驗的方法和初步測量結果，數據顯示在3.5km/s速度和地表常壓環境下，模型在距其約22倍特征長度位置產生的峰值超壓達到約35kPa。采用理想氣體假設的簡化計算仿真得到的音爆波形與試驗測量結果相似，但峰值超壓高于實測結果。

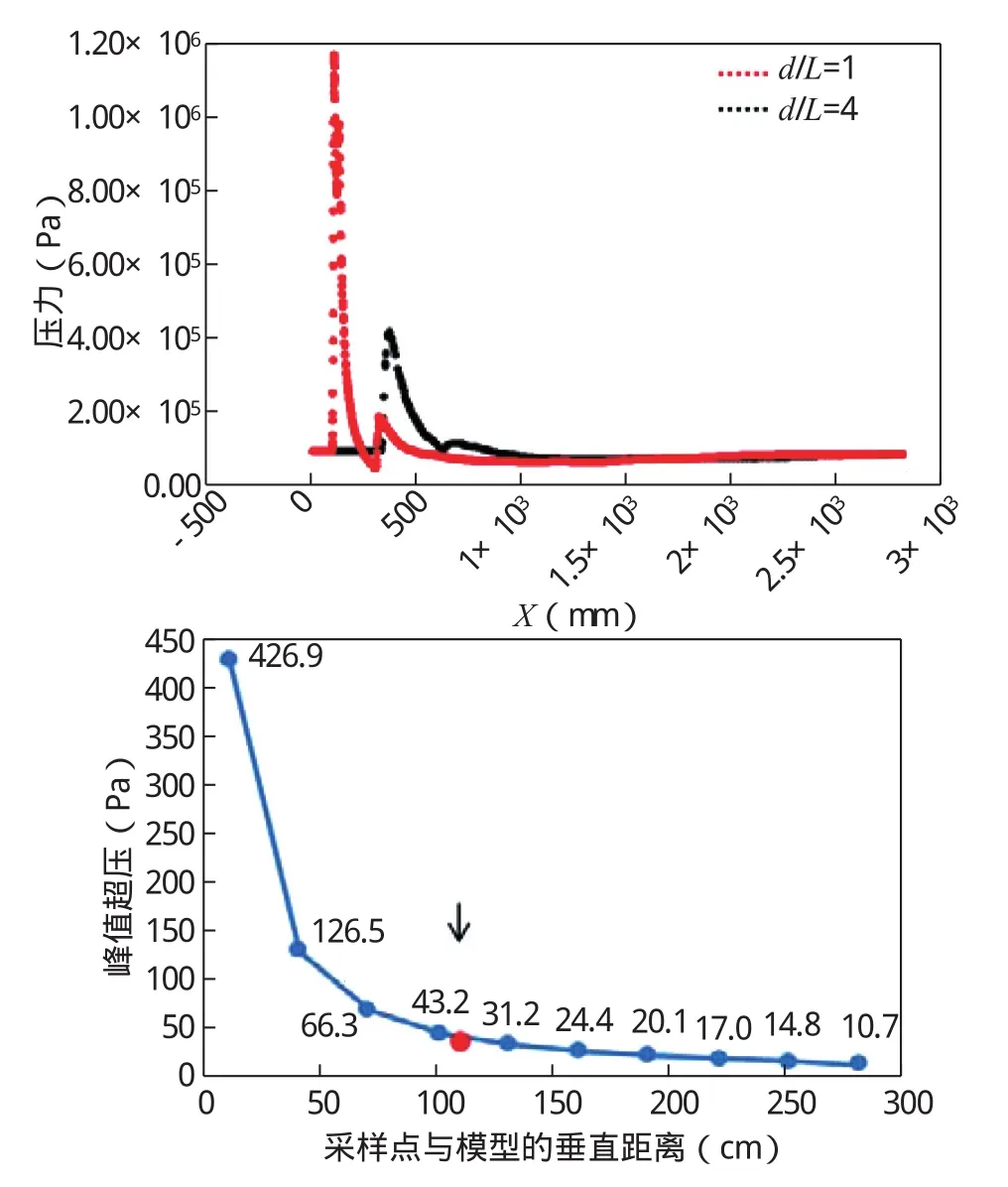
圖12 CFD計算得到的近場音爆波形及峰值超壓Fig.12 Near field sonic boom waveform and peak overpressure from CFD computation

后續，需從以下幾個方面進一步建立和完善隕石音爆計算方法和試驗手段，并開展對比驗證。一是發展考慮隕石材料、形狀和燒蝕特性的近場數值計算方法；二是開展更大測量范圍和更多采樣點的隕石音爆模擬試驗，獲取更加豐富和準確的實測數據；三是探索從近、中場到遠場的音爆傳播計算方法并開展對比驗證。