下穿古遺址隧道爆破振動預測模型及安全限界

費聿鵬

(中煤科工集團沈陽設計研究院有限公司，沈陽 110015)

近年來，交通軌道建設逐漸成為經濟可持續發展的新方向。在交通軌道建設過程中，工程爆破被廣泛應用于公路、鐵路隧道等掘進工程項目，但在應用過程中都面臨著一個丞待解決的重大問題——如何準確預測爆破振動強度大小并有效減小其對既有構筑物的影響。

爆破施工時炸藥爆炸產生的能量除了用來做有用功以外，其余能量轉變成有害效應被釋放出來，國內外學者[1-6]認為爆破施工所誘發的振動效應影響范圍及危害最大，因此準確預測爆破振動強度大小并探明其在介質中的傳播衰減規律對保護既有構筑物穩定而言顯得尤為重要。謝烽等[7]利用Anderson線性疊加模型建立符合現場實際的隧道近區振速計算模型，并驗證了其對隧道近區振速預測的可行性。李勝林等[8]分別采用薩道夫斯基公式和日本株式會社公式對比分析淺埋隧道爆破施工引起的地表振動衰減規律，認為采用日本株式會社公式對振速預測效果要比薩式公式更好。張士科等[9-11]通過建立基于基因表達式編程算法及遺傳算法優化BP神經網絡預測模型來擬合爆破振動參數與特征參量之間的非線性關系，并采用該模型對爆破振動特征參量進行預測。還有許多學者[12-14]為研究爆破振動的影響，采用數值模擬計算的方法建立模型，從而實現對爆破振動的動態預測分析。

上述學者對爆破振動預測方法進行了大量研究并取得了一定的研究成果，但所依據的理論不同，不能統一衡量每種方法的優缺點且不同的預測方法應用于特定的工程實際還缺乏一定的適用性，因此對爆破振動預測模型仍需進一步研究。筆者以朝凌客專翠巖隧道為依托，采用量綱分析法建立質點峰值振動速度預測模型，結合HHT法分析得出爆破振動的能量衰減規律；同時依據相關規范考慮最不利條件，確定爆破安全允許峰值振速，據此得出保護明長城遺址的安全限界閾值并提出相應的減振措施，以確保隧道爆破掘進施工對明長城遺址不造成影響。

1 振動速度預測模型的建立

衡量爆破振動強度大小的3個主要參數分別是：質點峰值振動速度v、質點振動頻率f和質點振動持續的時間t。據能量守恒定律可知，質點峰值振動速度v的大小直接影響振動強度的大小，因此以質點峰值振動速度作為爆破振動強度的研究對象。

目前國內普遍采用薩道夫斯基公式對質點峰值振動速度進行預測[15]：

(1)

式中：v為質點峰值振動速度，cm/s；Q為單段最大裝藥量，kg；R為測點到藥包中心的距離，m；k為與爆破場地條件有關的參數；α為爆破振動質點速度衰減系數。

當對復雜地質條件下監測的爆破振動數據進行分析時，由于各種因素對爆破振動波傳播的影響，如果仍采用式(1)預測質點峰值振動速度將會產生較大的誤差，為更準確地預測質點峰值振動速度，基于量綱分析法對式(1)進行修正。

1.1 相似準數方程的構建

隧道爆破掘進施工過程中爆破工藝參數、介質參數、炸藥參數及地質條件等因素都會影響爆破振動質點峰值速度的大小及其在介質中傳播的衰減速率[16-17]。因此，可將引起振動峰值速度變化的物理量總結為15個(見表1)。

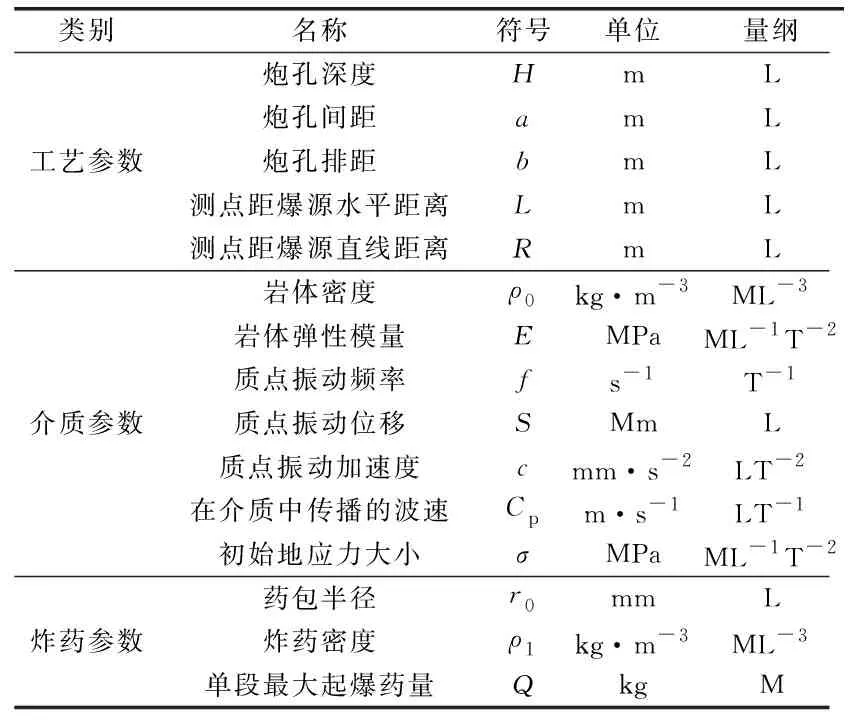
表1 物理量參數

基于量綱分析的π定理，任一物理量x的量綱公式可以用基本量綱的指數乘積形式來表示[18]。選取R、Q、Cp作為獨立量綱，將影響質點峰值振動速度的函數模型用15個獨立參量組合成的12個無因次數組πi(i=1～12)之間的函數關系來表示：

(2)

因此相似標準方程可寫成：

π=φ(π1，π2，π3，π4，π5，π6，π7，π8，π9，π10，π11，π12)

(3)

從式(3)可以看出，要想構建完整的相似準數方程十分復雜，但在實際工程中，往往要進行多次爆破才能得出該方程。在這種情況下，由于施工中每次爆破使用的工藝參數、炸藥種類和巖體特性變化不大，因此式(3)可簡化為

(4)

1.2 隧道爆破振速預測模型的構建

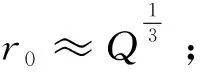
(5)

2 工程實例

2.1 工程概況

朝凌客專TJ-3標翠巖隧道位于錦州市凌海西北部，設計為雙線隧道，隧道進口里程為DK71+710，出口里程為DK73+187，全長1 477 m。隧道處于低山丘陵區，區段內山體多基巖裸露，植被稀疏，僅黃土覆蓋地區有人工林發育，最高山峰176.10 m，最低溝谷112.87 m，相對高差62.23 m，最大埋深62.62 m，隧道范圍內縱坡為3‰上坡。目前，隧道掘進掌子面處于里程DK72+650，設計在里程DK72+447處下穿明長城遺址，二者水平距離為203 m，區段內圍巖等級為Ⅴ級；明長城遺址與隧道走向呈一定角度相交，沿山脊起伏蜿蜒而過，交叉中心點處高程差為31.5 m，且明長城遺址保存較為完整，相對位置關系如圖1所示。

勃列日涅夫時期，政治體制倒退，使得蘇聯在斯大林時期就存在的“特權階層”進一步擴大與穩定，這一階層的人思想更趨僵化，這也成為阻礙整個體制改革的一個重要因素。

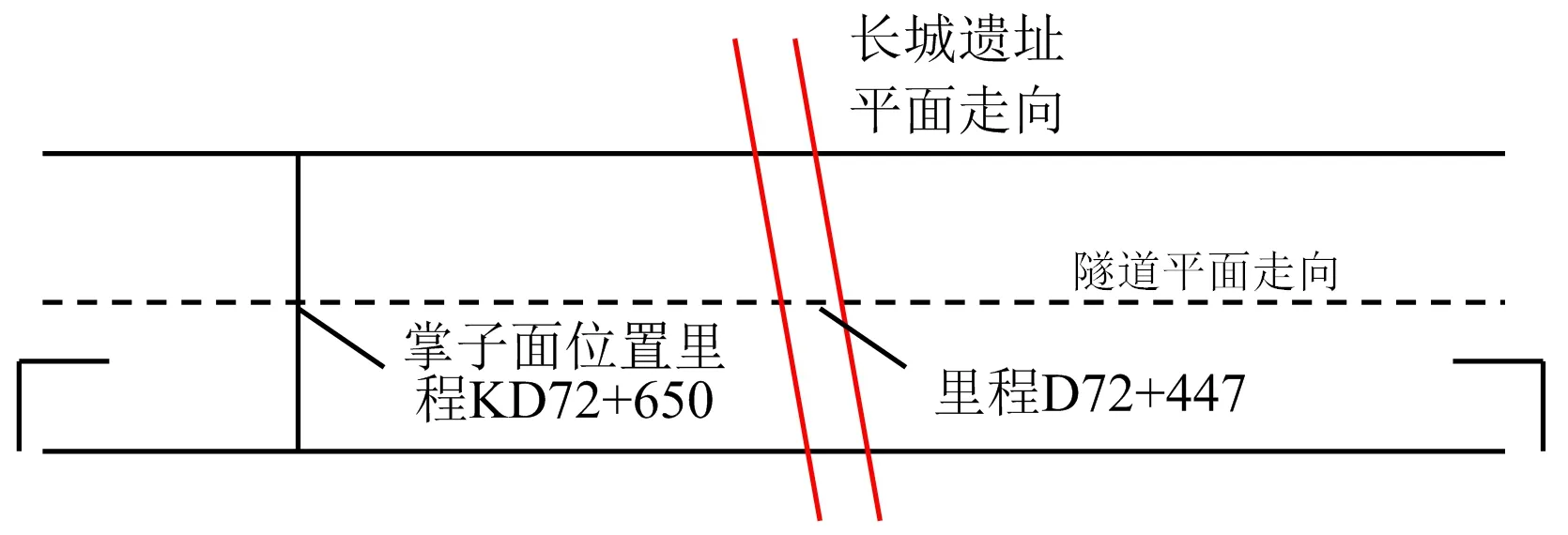
圖1 隧道與明長城遺址相對位置Fig.1 Relative location of the tunnel and the Great Wall site of the Ming Dynasty

2.2 爆破施工及振動監測概況

隧道掘進施工采用臺階爆破法(見圖2)。爆破施工采用2#巖石乳化炸藥、配套塑料導爆毫秒雷管及高能電容式起爆器，炮孔直徑42 mm，炮孔裝藥卷直徑32 mm、長度20 cm、每卷藥質量為0.2 kg，循環進尺為1.8 m，選用雷管段別范圍為MS1～MS15，起爆順序為先上后下。

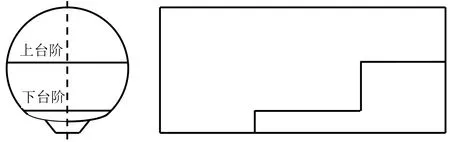
圖2 隧道爆破臺階布置Fig.2 Layout of tunnel blasting steps

現場監測采用9臺測振儀器，以隧道爆破掌子面為中心，測量范圍為0～50 m，呈交叉十字形對隧道上層地表進行爆破振動監測，同時采用2臺儀器對隧道與明長城遺址交叉點處進行監測；布置爆破測振儀時將x軸指向隧道的徑向，y軸指向隧道的軸向，z軸指向隧道的垂向，儀器布置如圖3所示。

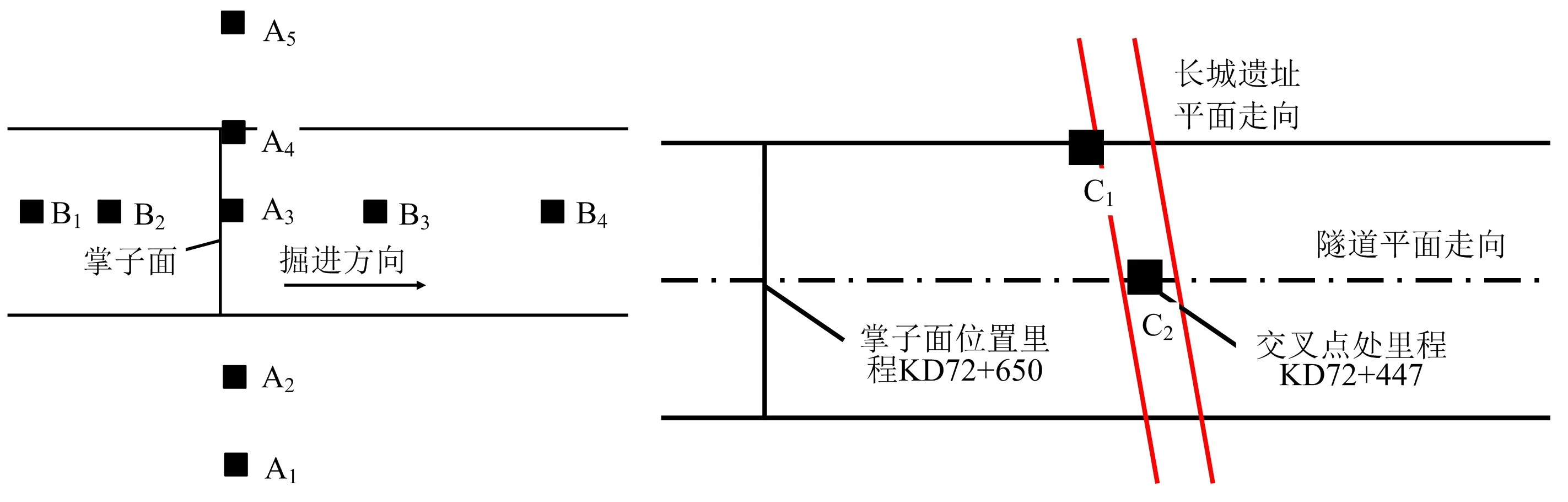
注：A1～A5、B1～B4、C1～C2為測振儀位置編號。圖3 現場監測儀器布置Fig.3 Layout of field monitoring instruments

盧文波等[21-22]對在不同自由面條件下爆破產生的振動信號進行頻譜分析，得出隨著自由面數量的增加，振速隨之減小、主頻增大且持續時間變短等結論。針對本工程實際情況，由于上臺階只有一個自由面，而下臺階具有兩個自由面，因此可認為臺階爆破在相同單段最大起爆藥量的條件下，上臺階爆破所引起的振動效應較大。為能夠準確反映爆破振動強度的大小，采用上述監測方案進行現場試驗，并根據毫秒導爆雷管的延時時間范圍[23]，現提取上臺階雷管段別MS5和MS7對應時刻的質點峰值振動速度，試驗數據剔除無效數據后如表2所示。

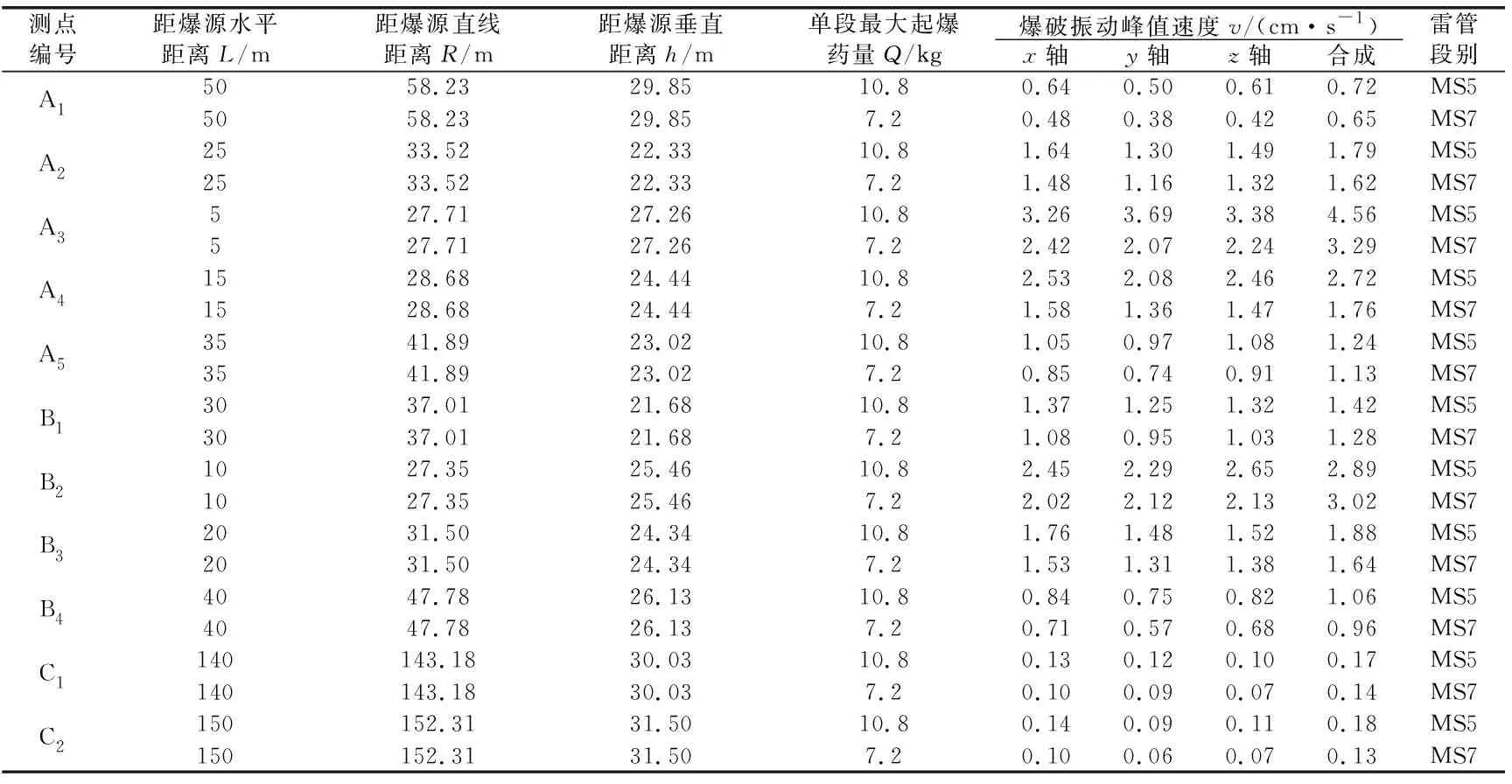
表2 現場監測試驗數據

3 信號分析及安全限界閾值研究

3.1 監測數據回歸分析

實際上，國內采用的薩道夫斯基經驗公式是根據硐室爆破提出的，相關參數值需要通過回歸運算獲取。考慮明長城遺址處C測點較A和B測點距離較遠，如將3個測點數據一起進行回歸運算，其結果可能會引起較大誤差；因此利用A、B測點數據進行非線性回歸運算，得出薩氏經驗公式(1)和新建公式(5)的參數值及相似系數R(見表3)，非線性回歸如圖4～圖5所示。

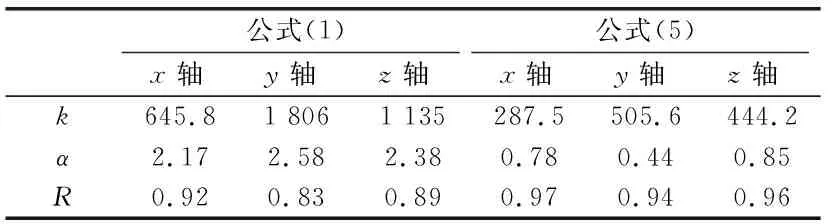
表3 回歸系數

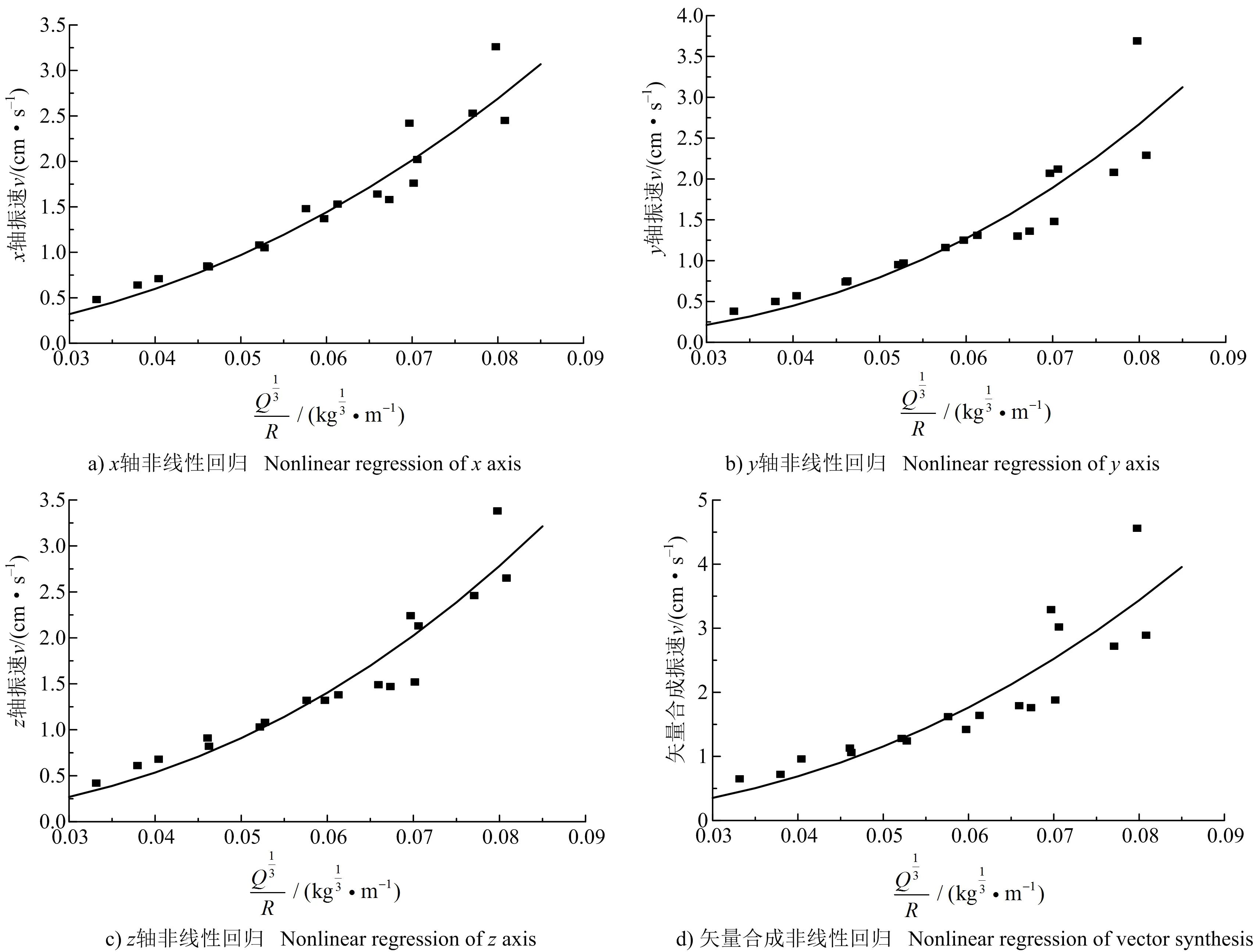
圖4 公式(1)非線性回歸Fig.4 Formula (1) nonlinear regression

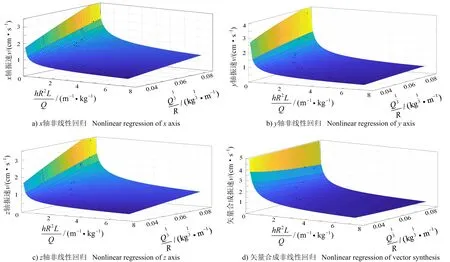
圖5 公式(5)非線性回歸Fig.5 Formula (5) nonlinear regression

因此可得公式(1)為

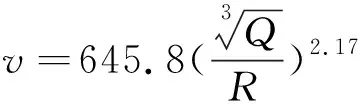
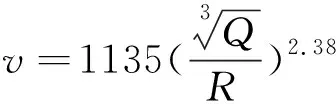
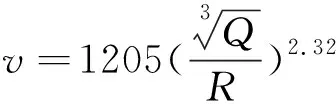
(6)

公式(5)為

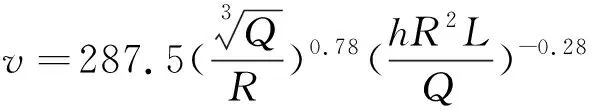
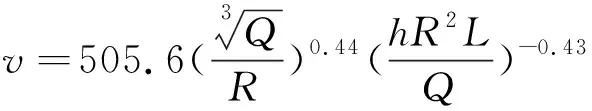
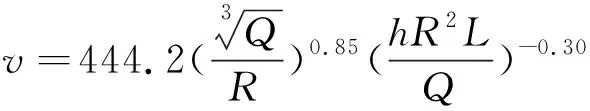
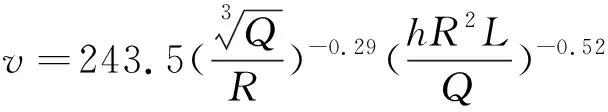
(7)

3.2 非線性回歸運算準確度評價

由于爆破振動波在巖土體內傳播過程中差異性較大，非線性回歸運算結果勢必存在一定誤差，因此用式(6)和式(7)預測各測點振速并與實測數據進行相對誤差分析，從而判斷回歸運算及預測的準確性。ε為相對誤差，εi=|vi預-vi實|/vi實，測點實測數據參照表2，各方向誤差分析結果如表4所示，各方向相對誤差區間及平均誤差如表5所示。

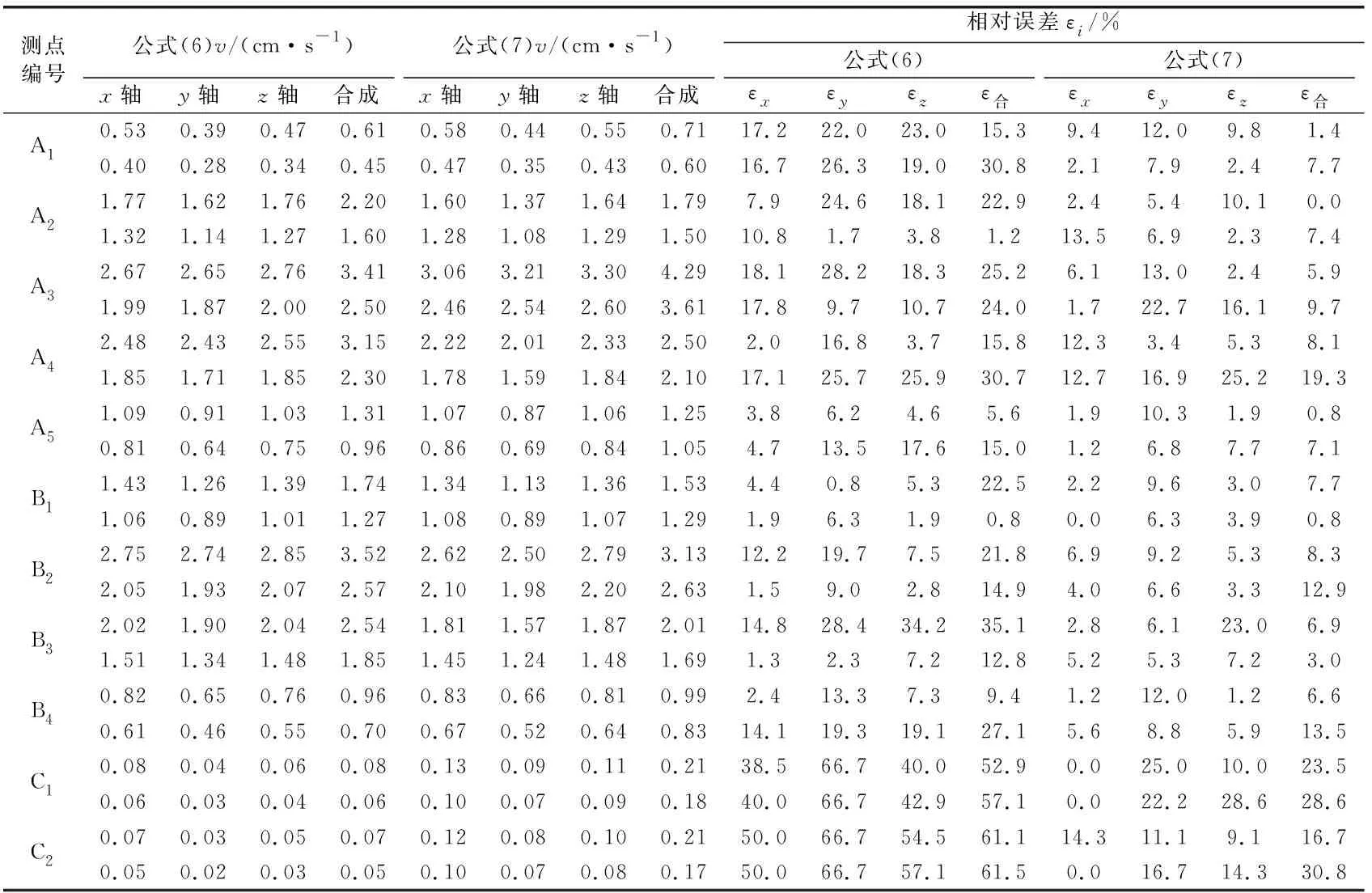
表4 誤差分析結果

表5 誤差對比

從表5對比結果可以看出式(1)和式(5)的非線性回歸運算結果都較為精確；采用非線性回歸運算得出的式(7)對振速預測結果較式(6)誤差更小，二者最大平均相對誤差分別為15.9%和40.4%，尤其是對明長城遺址與隧道走向交叉點處振速的預測；同時也證明了采用量綱分析法建立的爆破振速預測模型可應用于工程實踐，且其較傳統的薩氏公式對振速的預測更為準確。

3.3 爆破振動強度信號分析

近年來，采用希爾伯特-黃變換法(簡稱HHT法)對短時性、非線性及非平穩性的爆破振動信號進行分析是在傅里葉變換基礎上的重大突破[24-25]。HHT分析法不需要固定先驗信號基底，并且能夠描繪出信號的時頻譜圖、Hilbert能量譜圖等，是一種更具有自適應性的時頻局域化分析方法[26-27]。

為探明爆破振動強度沿隧道各方向的衰減規律，選取上述測點中A2、A3和B3的振動信號進行Hilbert變換處理，在該分解變換過程中剔除高頻噪聲和殘余項，最終得出上述測點各方向的時間—頻率—信號幅值三維圖(簡稱Hilbert譜)及瞬時能量圖，由于篇幅有限，僅給出測點A2處圖形(見圖6)。

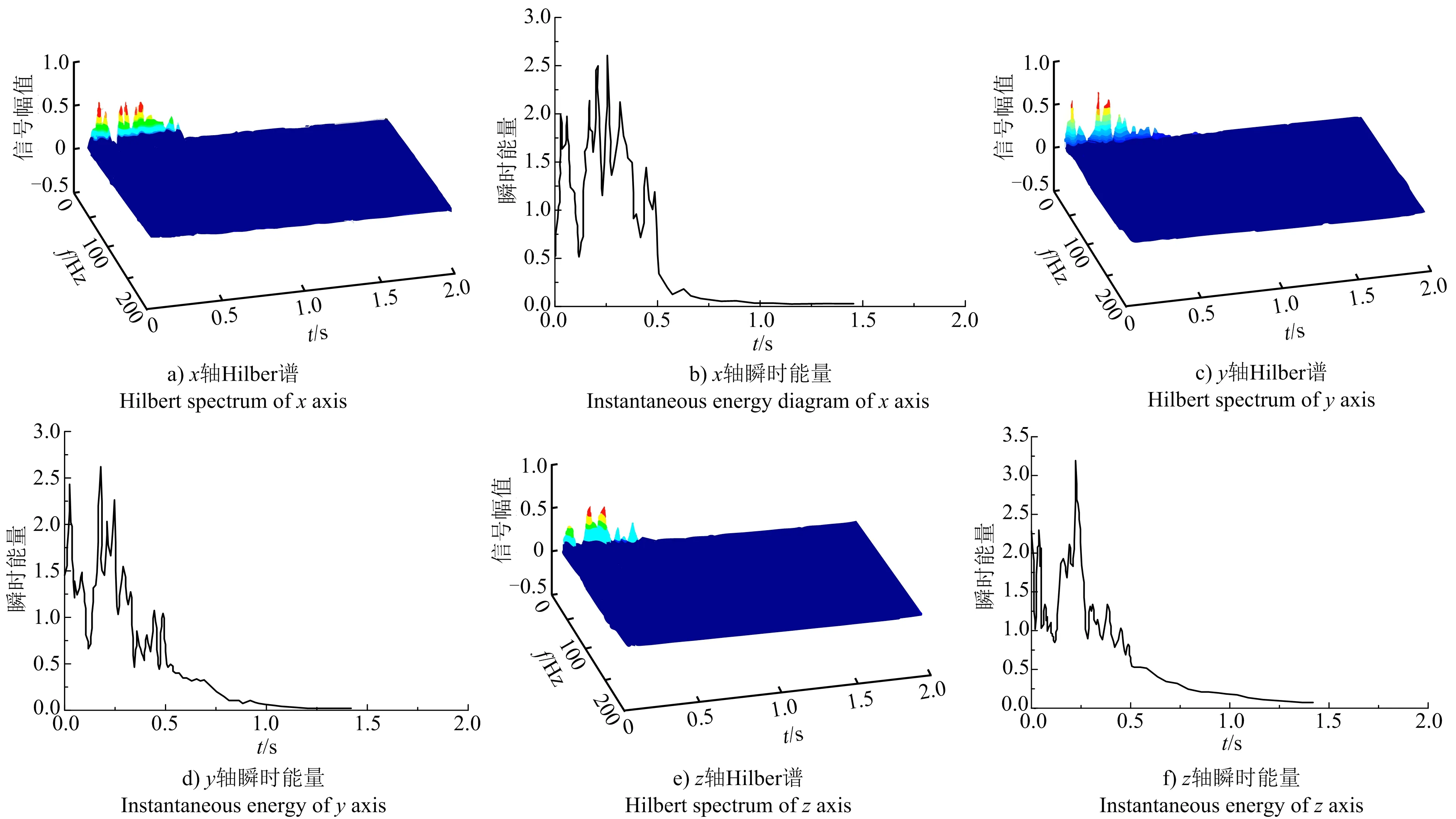
圖6 A2測點各方向Hilber譜與瞬時能量Fig.6 Hilbert spectrum and instantaneous energy of A2 measuring point in all directions

根據圖6中各測點各方向的Hilbert譜可以看出實測爆破振動波的頻率主要分布在20 Hz以內，最大幅值的頻率集中在10～20 Hz，最大幅值出現的時間在0.5 s以內。從爆破振動瞬時能量的角度分析其衰減規律會顯得更加清晰，從圖6～圖8中匯總出各測點x軸、y軸和z軸的最大瞬時能量值及對應的時刻，其結果如表6所示。

表6 測點瞬時能量-時刻

由表6可知，A3測點各方向的瞬時能量值最大，原因是A3測點距爆源最近，因此爆破振動波傳播至A3測點的距離較短，能量損失較少，振動強度衰減速率較小；對比各測點x軸瞬時能量值可以看出，爆破振動能量沿隧道徑向衰減速率要快于軸向；同時對比y軸與z軸瞬時能量值可以分別得出，y軸振動強度沿隧道徑向和軸向的衰減速率相差不大，z軸振動強度沿隧道軸向的衰減速率比徑向衰減速率大。

產生上述現象的原因是：爆源正上方的區域，由于隧道埋深較淺，爆破振動波在傳播過程中先受到上覆巖土體初始地應力的阻礙作用，導致振動波能量部分損失；且上方表土較為松散多種植果樹木，表土下部多為裂隙較發育的巖體，迫使振動波傳播發生透反射，而透射入巖土體繼續傳播的振動波，由于巖土體內裂隙、節理的存在，使爆破振動波強度再次大幅衰減；因此振動波傳播隨著距爆源水平距離的增大，能量損失越多，振動強度衰減速率也十分迅速。

3.4 保護明長城遺址安全限界估算

從上述研究結果可知，爆破振動最大幅值的頻率集中在10～20 Hz，而相關規范[15]中規定一般文明古跡在該頻率段內安全允許質點振動速度為0.2～0.3 cm/s；考慮最不利因素，取安全允許振速為0.2 cm/s，利用回歸得到的公式(7)繪制出在安全振速范圍內單段最大起爆藥量與安全距離的關系(見圖7)。

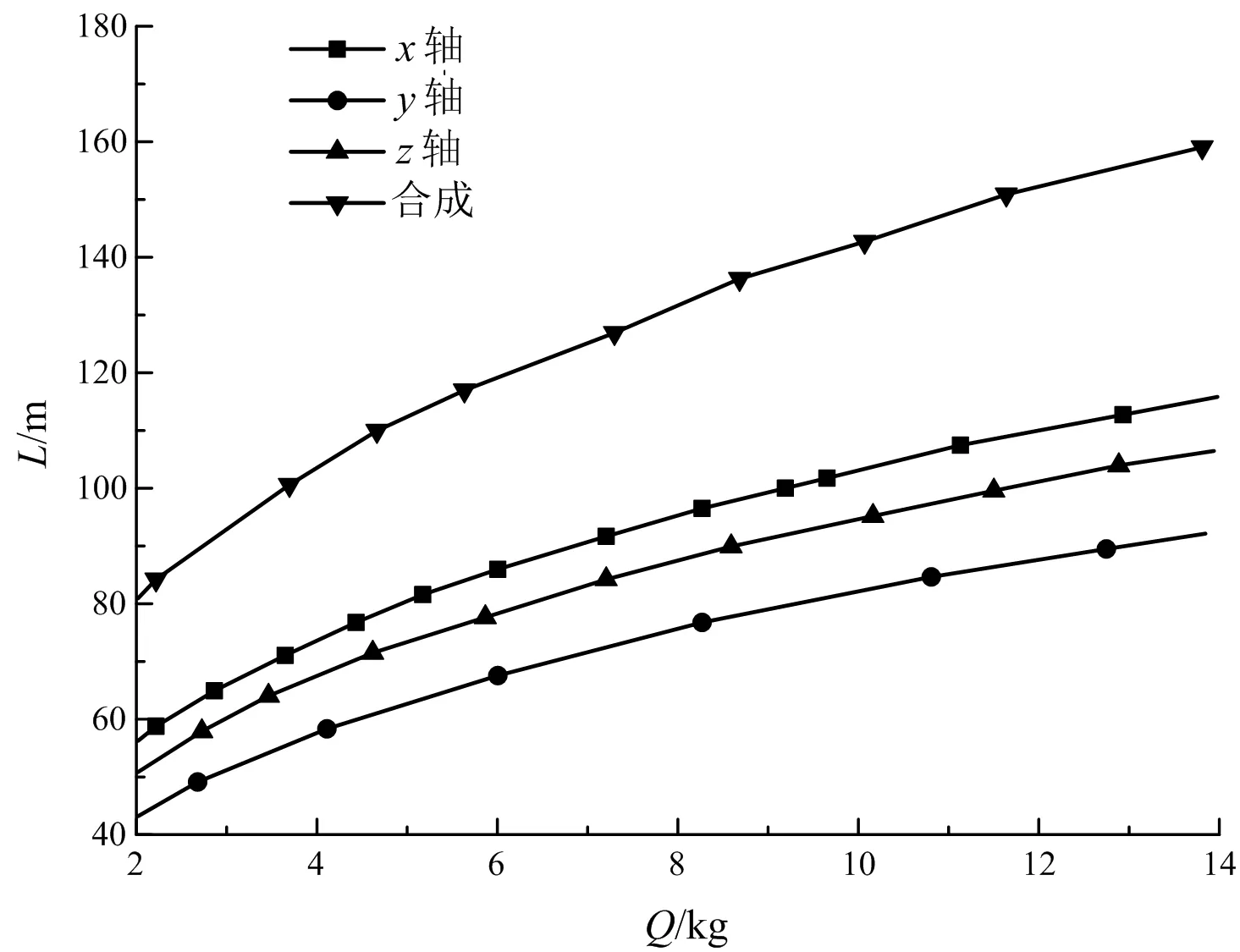
圖7 安全距離與單段最大起爆藥量關系(v=0.2 cm/s)Fig.7 Relationship between safety distance and single maximum detonating charge(v = 0.2 cm/s)

由圖7知：在安全允許振速v=0.2 cm/s條件下，單段最大起爆藥量與安全距離呈非線性函數關系；且隨著單段最大起爆藥量的增加，安全距離大小呈現：矢量合成方向>x軸>z軸>y軸，即在單段最大起爆藥量確定的條件下，應用式(7)中的矢量合成振速預測公式計算所需的安全距離最大；據此可以認為采用該公式的計算結果作為保護明長城遺址的安全距離閾值相對具有安全可靠性。同時依據上述研究結果，計算出保護明長城遺址安全距離的參考范圍(見表7)。

表7 安全距離

根據目前施工方案，從表6中可以得出隧道爆破掘進至距明長城遺址192 m時，必須采取相應措施以減小爆破振動效應的影響。減小爆破振動效應的措施：①選取合適的掏槽形式，合理布置孔網參數，并嚴格控制單段最大起爆藥量；②優化起爆網路和裝藥結構，采取孔內延時爆破技術，合理設置起爆延時時間，以提高爆破振動主振頻率，從而增大安全允許振速閾值；③建議采用高精度導爆管雷管或電子數碼雷管，以保證雷管延時時間更加精確，降低爆破振動波能量疊加的機率。

4 結論

1)采用量綱分析法建立的爆破質點峰值振動速度預測模型，運用非線性回歸運算得出模型相關參數，并與傳統薩氏公式進行準確度評價分析，證明了新建公式預測的準確性及應用于工程實際的可行性。

2)應用HHT法對爆破振動信號進行Hilbert處理，繪制出時間—頻率—信號幅值三維圖和瞬時能量圖，進而得出爆破振動強度沿隧道徑向、軸向及垂向傳播的特征規律，為分析爆破振動強度衰減規律提供了一種新方法。

3)依據相關規定及爆破振動強度的衰減規律，計算得出隧道爆破掘進掌子面在距離明長城遺址192 m處時，必須采取相應的減振措施以確保爆破施工對明長城遺址不造成影響。