PCA-BP算法在地面爆破振動中的應用

趙紅夢，姜志俠

(長春理工大學理學院，長春130000)

隨著科技的發展與進步，礦場開采等活動所引起的地面爆破振動對生產和生活環境的影響引起大眾的廣泛關注；目前評估地面振動以及損害最重要的兩個參數為爆破質點峰值振動速度(PPV)和頻率[1]。傳統的地面振動研究方法是通過對爆破振動相關有效數據進行回歸分析，然后通過回歸分析得到的薩道夫斯基經驗公式進行預測[2]，現實中質點峰值振動速度本身與很多因素有關，而常用的經驗公式考慮的影響因素較少，導致其預測結果的誤差較大。

基于常用公式的局限，眾多學者提出應用BP神經網絡算法解決預測爆破質點峰值振動速度問題[3]。其中郭連軍等[4]利用優化的神經網絡建立爆破的預測模型；施建俊等[5]將MATLAB與VB技術相結合，開發得到爆破質點峰值振動速度預測模型；孟陸波等[6]基于人工神經網絡算法建立了爆破質點峰值振動速度預測模型；張藝峰等[7]建立了針對爆破質點峰值振動速度以及主頻的預測模型。

針對目前研究現狀，筆者將主成分分析(PCA)與BP神經網絡算法結合在一起，提出了一種新的預測爆破質點峰值振動速度的算法,記為PCA-BP算法；其中主成分分析為一種利用降維思想提取數據中方差貢獻率較大特征的方法[8]。該算法整體步驟為首先采用主成分分析方法對影響爆破質點峰值振動速度的眾多因素進行分析和簡化，再結合BP神經網絡算法進行預測，并且將預測結果與傳統經驗公式預測結果進行對比分析。

1 PCA-BP算法提出

1.1 PCA算法

PCA算法最核心的思想就是降維，是通過正交變換將指標減少的多元統計分析方法[9]。

現有p個變量x1,x2,…xp，n個樣品的數據陣為

(1)

(2)

將p個變量綜合為p個新的綜合變量，即

(3)

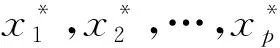
1.2 BP神經網絡算法

BP算法由輸入層、輸出層、隱藏層3部分構成，BP算法的學習過程由正向、反向傳播組成[11]。

設輸入模式為x=(x1,x2,…,xn)T，算法設置隱藏層有h個單元，隱藏層的輸出為y=(y1,y2,…,yh)T，輸出層有m個單元，網絡輸出為z=(z1,z2,…,zm)T，目標輸出為t=(t1,t2,…,tm)T，隱藏層到輸出層的傳遞函數為f,輸出層的傳遞函數為g，于是可得：

(4)

式中：yj為隱藏層第j個神經元的輸出;w0j=θ,x0=-1。

(5)

式中：zk為輸出層第k個神經元的輸出;此時網絡輸出與目標輸出的誤差為

(6)

1.3 PCA-BP算法

首先采用PCA方法對影響爆破質點峰值振動速度的參數進行降維處理[12]，再以PCA算法計算的綜合評價得分作為BP算法輸入的初始數據，最后通過BP神經網絡算法對爆破質點峰值振動速度進行預測。

PCA-BP算法主要步驟如下：

1)對地面爆破振動的輸入數據進行標準化處理；

2)計算數據相關系數矩陣的特征向量；

3)選擇p個特征向量構成主成分；

4)由主成分綜合評價得分和BP參數隨機選取第k個輸入數據作為輸入及對應期望輸出；

5)利用隱藏層各神經元的輸入和輸出，計算誤差函數ε對輸出層的各神經元的偏導數和誤差函數對隱含層各神經元的偏導數，分別為

6)計算從隱藏層到輸出層的權值

wjk(t+1)=wjk(t)+ηδkyj，

再計算從輸入層到隱藏層的權值

wij(t+1)=wij(t)+ηδjxi；

7)判斷目標誤差是否滿足要求，當誤差達到預設精度則停止計算；否則，返回到第5步，進入下一輪學習。

2 案例分析

現引用文獻[5]中的20組實測地面爆破振動數據(見表1)進行研究，影響爆破振動的參數比較多，將爆心距x1、高程差x2、總藥量x3、炮孔深度x4、單段最大量x5作為研究的自變量，以爆破質點峰值振動速度作為因變量，通過PCA方法提取主成分，利用BP神經網絡算法進行預測。

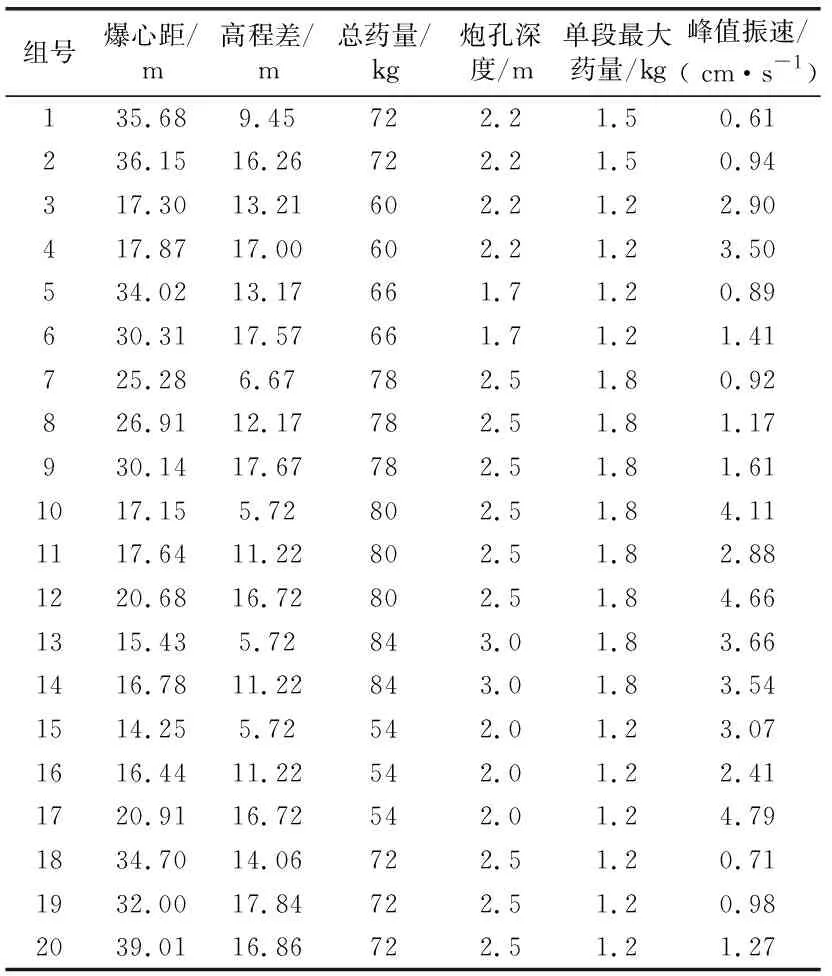
表1 爆破振動數據

表1中，選擇前15組數據作為訓練數據，后5組作為測試數據，通過訓練數據得出的結論預測后5組數據的爆破質點峰值振動速度；并將預測結果與傳統薩道夫斯基經驗公式所得結果進行對比分析。

2.1 相關性分析

首先進行原始數據的標準化處理，標準化處理公式為

(7)

式中：x′為標準化后的數據;x為原始數據;u為樣本均值;σ為樣本標準差.

根據正態分布的基本性質，有x～N(u,σ2)，則有

(8)

原始數據集標準化為接近于正態分布(均值為0，方差為1)的數據集，然后對其數據進行相關性分析，得到相關系數如表2所示。

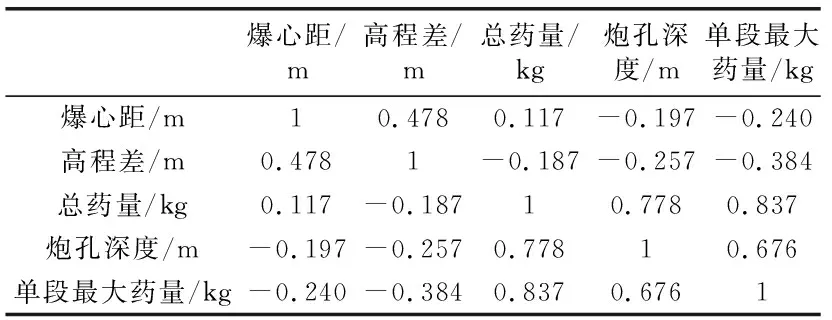
表2 相關系數

由表2知單段最大藥量與總藥量、炮孔深度相關系數較高，所以適合做主成分分析。

2.2 主成分分析

1)主成分選取。首先利用碎石圖(見圖1)選取主成分。

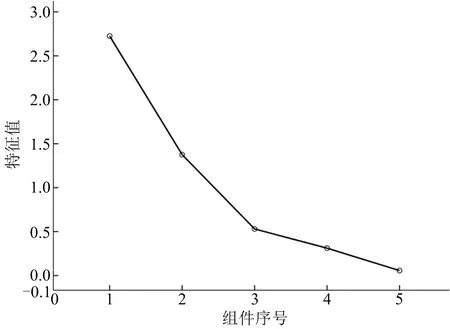
圖1 碎石圖Fig.1 Break store chart

由圖1知，組件序號在4到5時圖形區域平緩，初步判定可以選擇3～4個主成分,其次進行累計方差貢獻率研究(見表3)。

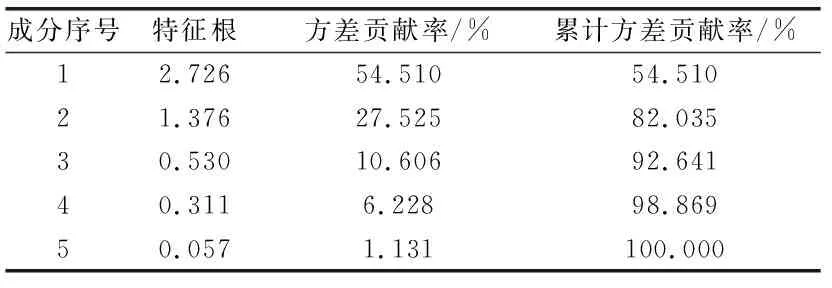
表3 累計方差貢獻率

可以看出在選擇3個主成分時候，保留了原始變量92.641%的信息。利用新的3個主成分代替原來的5個變量，從而起到降維的作用[13]。

2)主成分得分。第一步進行因子載荷陣的求取，利用軟件得到因子載荷矩陣(見表4)。

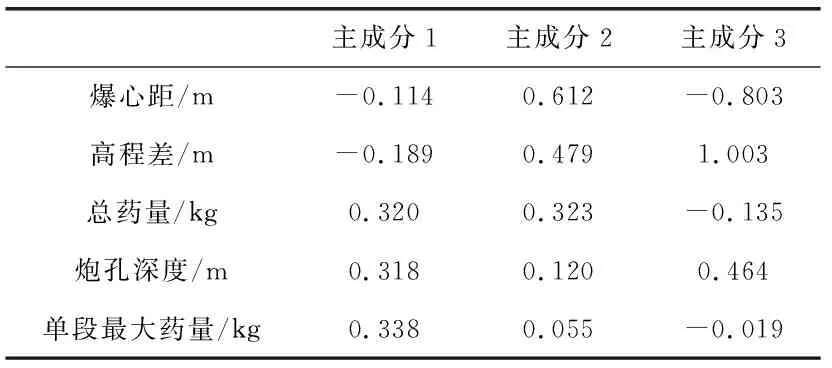
表4 因子載荷陣

根據因子載荷陣計算主成分得分公式：

(9)

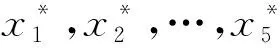
從而根據主成分得分公式以及方差貢獻率分別計算20組數據的綜合評價得分為：-7.04、3.21、-11.25、-5.56、-18.33、-11.53、2.38、10.6、18.76、2.38、10.66、18.82、14.15、22.38、-29.47、-21.27、-13.17、1.47、7.29、5.51。

2.3 PCA-BP算法

將主成分分析提取的3個主成分，經計算得綜合評價得分作為BP算法初始數據的輸入，通過訓練組數據(前15組)得出的結論預測測試組(后5組)數據。構建一個3層BP神經網絡對地面振動后5組數據(見表1)的爆破質點峰值振動速度進行預測，其中輸入層結點數為3個，隱藏層結點數為8個，激活函數選擇‘tansig’;輸出層結點數為1個，激活函數選擇‘logsing’。

采用梯度下降動量和自適應lr算法‘tansig’訓練BP網絡。學習率為0.05，目標誤差為0.625×10-3，最大迭代次數為1 000，使用MATLAB軟件進行計算。前15個網絡輸出與實際輸出對比如圖2所示。

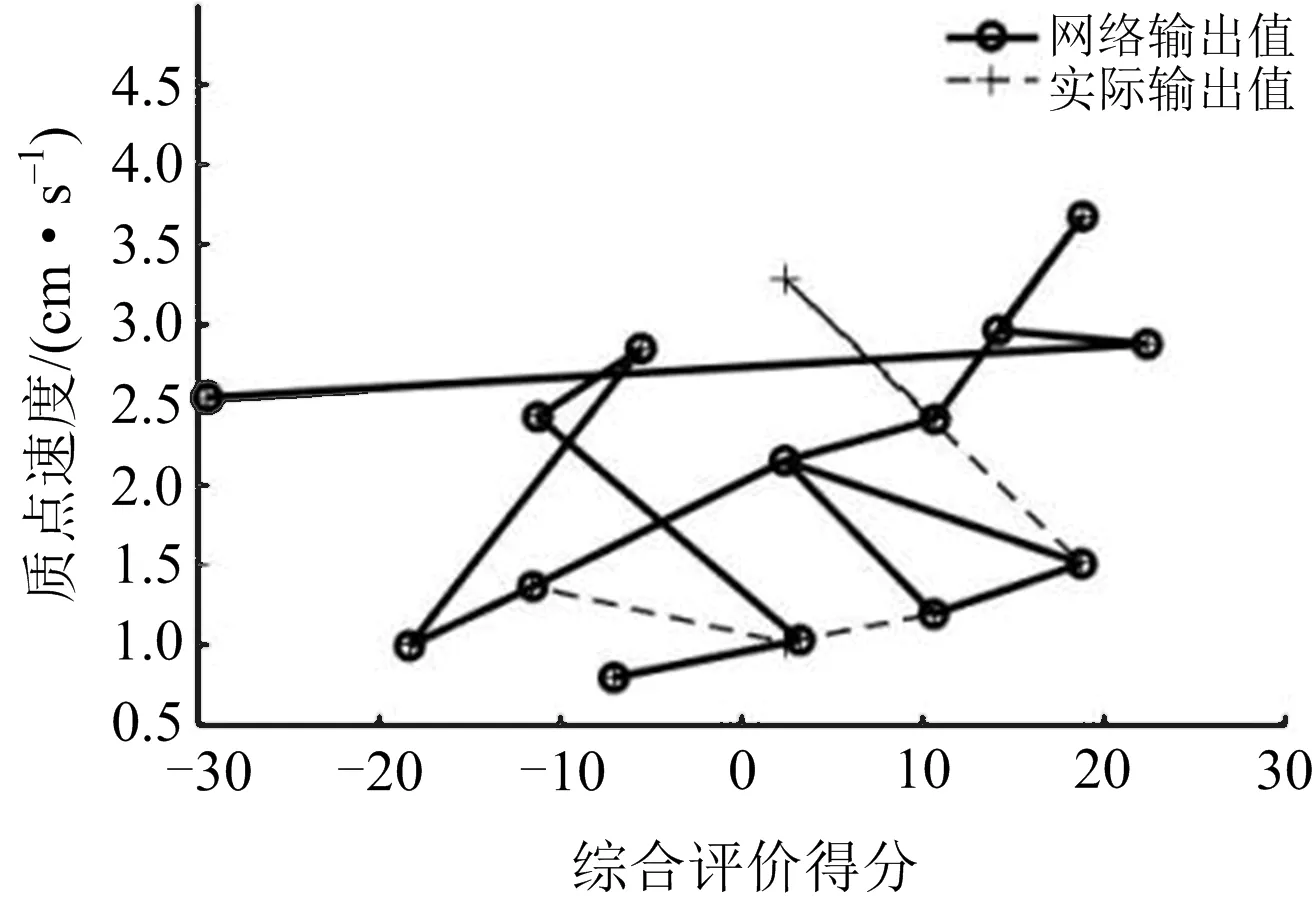
圖2 前15個網絡輸出與實際輸出對比Fig.2 Comparison of the first 15 network outputs and the actual output

地面爆破質點峰值振動速度預測結果與期望目標的關系如圖3所示。

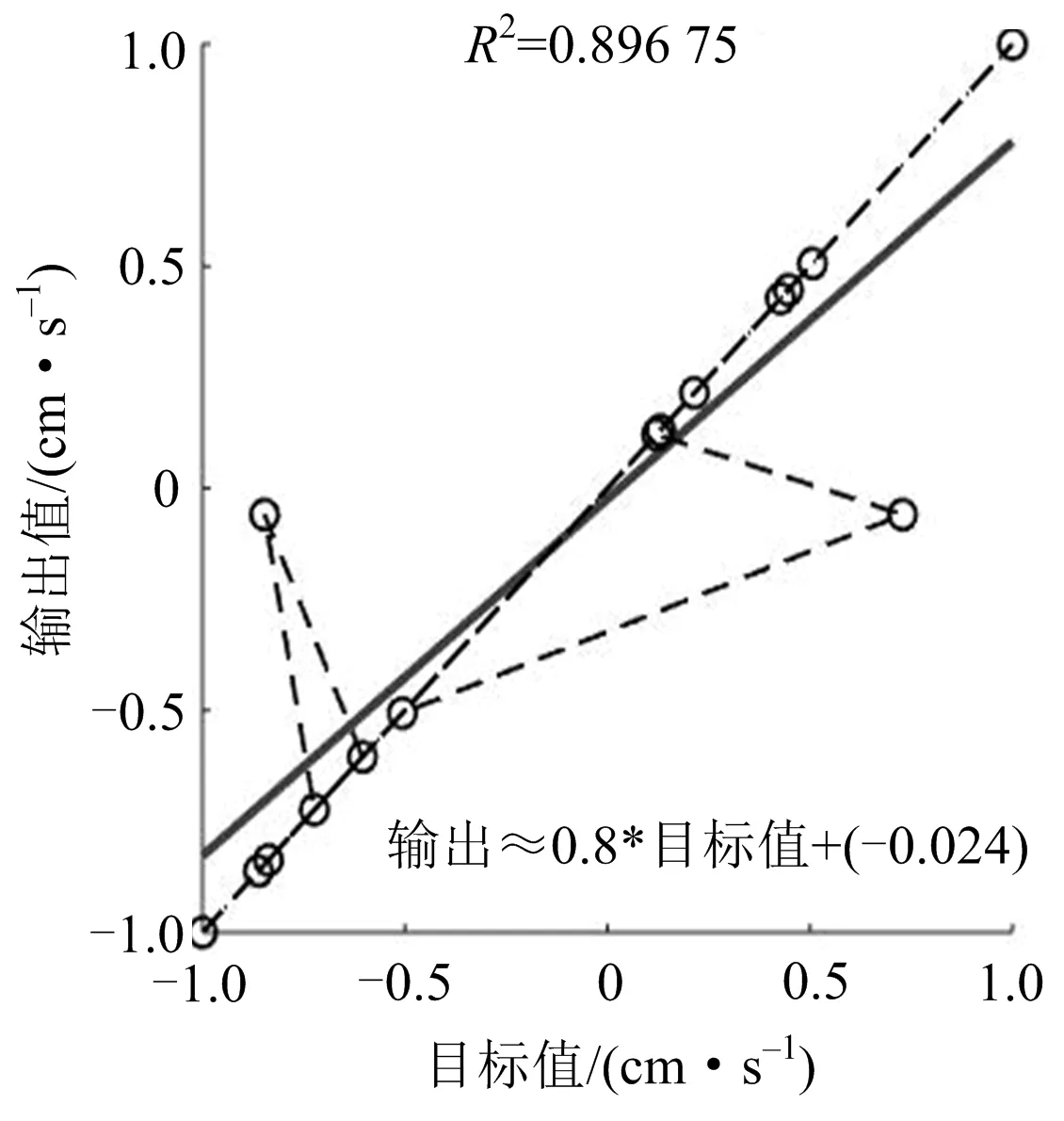
注：實直線為預測結果擬合的線性曲線，散點圖構成的虛線為實際值擬合而成。圖3 振速預測與期望目標關系Fig.3 Relationship between vibration speed prediction and desired target

利用PCA-BP算法經MATLAB計算可得測試數據(后5組)預測結果值分別為2.349 2、4.929 6、0.771 2、1.150 3、1.421 4。將預測結果與期望目標擬合成線性函數，計算得二者的相關系數達到 0.896 75(理想狀態是相關系數等于1時)[13]，說明預測結果的可信度較高。

3 對比分析

傳統薩道夫斯基經驗公式[14]為

(10)

式中：k,α為經驗系數；Q為單段藥量；R為測點到爆心的距離。

從而利用對數變換

(11)

令

公式變為回歸方程

y=b+αx

從而得到預測公式為

y=2.551+1.747x

(12)

利用傳統經驗公式計算后5組數據預測結果為1.60、1.34、0.91、0.97、0.83，具體回歸分析結果如表5所示。

表5 回歸分析結果

將傳統薩道夫斯基經驗公式[15]以及PCA-BP算法預測結果進行對比分析(見表6)，這里以測試數據(后5組)預測結果的相對誤差、平均誤差作為參照，可看出利用PCA-BP算法預測的相對誤差分別為2.52%、2.83%、7.94%、14.80%、10.65%，平均相對誤差為7.748%；傳統經驗公式的相對誤差較高，分別為33.61%、72.03%、21.97%、1.02%、34.64%，平均相對誤差為32.654%；除了第19組的相對誤差略高于用傳統經驗公式預測的相對誤差外，其他組利用PCA-BP算法預測的相對誤差均較小；這說明PCA-BP算法預測模型有效性較高。

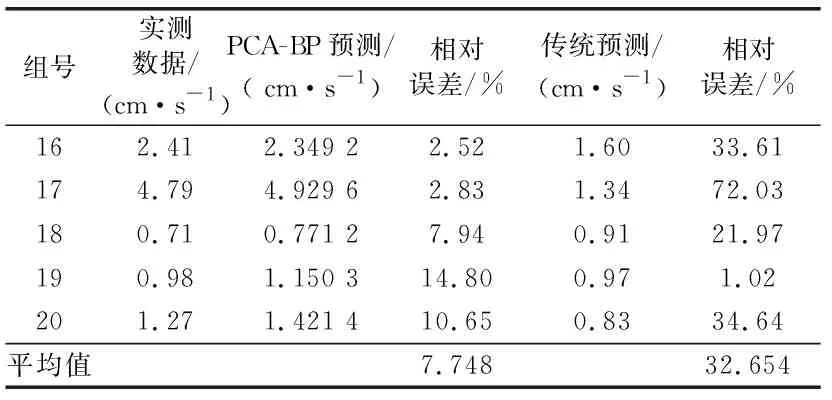
表6 預測結果對比分析

4 結語

PCA-BP算法解決了在預測爆破質點峰值振動速度中輸入數據較多，各個輸入變量之間存在多重共線性和相關性的問題。在案例分析中，通過對輸入數據進行主成分分析提取主成分特征向量，計算綜合評價得分作為BP算法的輸入，并與傳統薩道夫斯基經驗公式預測相比，PCA-BP 算法綜合考慮影響地面爆破振動的因素，使得預測結果更加合理，結合主成分分析和BP神經網絡算法的預測結果平均相對誤差為7.748%，小于用薩道夫斯基經驗公式進行預測的平均相對誤差32.654%，故說明，將PCA-BP算法應用到爆破振動工作中是比較可行的。