一道解析幾何題的拓展探究

陜西 韓紅軍

高三教學中，我們遇到一道解析幾何試題如下：設圓x2+y2-4x-60=0的圓心為F2，直線l過點F1(-2,0)且與x軸不重合，交圓F2于C，D兩點，過點F1作CF2的平行線交DF2于點E.

(Ⅰ)求|EF1|+|EF2|的值；

(Ⅱ)設點E的軌跡為曲線E1，直線l的斜率為1，且與曲線E1相交于A，B兩點，與直線x=-8相交于M點，試問在橢圓E1上是否存在一定點N，使得k1，k3，k2成等差數列(其中k1，k2，k3分別是指直線AN，BN，MN的斜率).若存在，求出N點的坐標；若不存在，請說明理由.

【分析】此題屬于解析幾何中的存在性問題，也是高考的熱點問題之一，第(Ⅰ)問構思巧妙，重在考查平面幾何基本知識，考查邏輯推理核心素養；第(Ⅱ)問是以探究的方式，考查直線與橢圓的位置關系，同時將等差數列融入其中.

【解析】(Ⅰ)因為|F2D|=|F2C|，F1E∥CF2，所以∠F2DC=∠F2CD=∠EF1D，所以|EF1|=|ED|，所以|EF1|+|EF2|=|ED|+|EF2|=|DF2|，又因為圓F2的半徑為8，即|DF2|=8，所以|EF1|+|EF2|=8.

一、逆向拓展探究

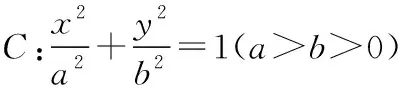
根據解題習慣，我們將左焦點、左準線分別換成右焦點、右準線，進一步深入探究上述命題的逆命題是否成立？

二、類比拓展探究

如果將上述的橢圓換成雙曲線或拋物線，又會得出什么樣的結論呢？此結論是否正確呢？于是我們進行進一步探究，得到如下命題：

以上這些變式是從高考經常考查的橢圓熱點問題入手思考的，首先考慮能否將問題一般化，其次考慮能否將問題進行推廣，將橢圓變成雙曲線、拋物線后，情況如何？這樣才能找到規律，將問題理解得更透、把握得更全、思考得更深.這些變式環環相扣，層層深入，落點很高，實現由知識向能力、能力向素養的轉化.