2019年北京卷理科第18題圓錐曲線的探究與推廣

廣東 蔡芝芝

一、題目呈現

(2019·北京卷理·18)已知拋物線C:x2=-2py經過點(2,-1).

(Ⅰ)求拋物線C的方程及其準線方程；

(Ⅱ)設O為原點，過拋物線C的焦點作斜率不為0的直線l交拋物線C于兩點M，N，直線y=-1分別交直線OM，ON于點A和點B.求證：以AB為直徑的圓經過y軸上的兩個定點.

二、題目分析

本題以拋物線為載體考查直線與圓錐曲線的綜合應用.第(Ⅰ)問求曲線方程，屬于容易題；第(Ⅱ)問是圓過定點問題，考查拋物線與圓的定義、性質及直線與圓錐曲線的位置關系，并考查數形結合、函數與方程和化歸與轉化的數學思想方法，同時考查運算求解能力和綜合運用數學知識解決問題的能力.試題結構非常簡單，題干簡潔，求解的思維過程體現了對解析幾何核心內容和通性通法的考查.本文通過解法分析、規律探索和規律推廣等方面對本試題進行分析.

三、解法分析

(Ⅰ)因為拋物線C:x2=-2py經過點(2,-1)，

所以4=2p，所以拋物線C的方程為x2=-4y，準線方程為y=1.

(Ⅱ)解法一：證明：因為拋物線的焦點為F(0,-1)，

設直線l的方程為y=kx-1(k≠0).

綜上，以AB為直徑的圓經過y軸上的定點(0,1)和(0,-3).

評注：把題目中的幾何條件用代數形式(坐標)表示出來，利用韋達定理進行整體代換是解析幾何中最常用的方法之一.“以AB為直徑的圓經過y軸上的定點D”可轉化為“∠ADB=90°”，再利用向量數量積求值，也可以用斜率之積來轉化運算.體現了化歸與轉化的數學思想方法在解析幾何問題中的應用.

解法二：因為拋物線的焦點為F(0,-1)，

所以設過焦點的直線l的方程y=kx-1(k≠0).

剩下部分與解法一相同，不再重復.

解法三：證明：因為拋物線的焦點為F(0,-1)，

所以設過焦點的直線l的方程為y=kx-1(k≠0).

所以，以AB為直徑的圓的方程為(x-2k)2+(y+1)2=4(k2+1)，

令x=0得4k2+(y+1)2=4k2+4，解得y=-3或y=1.

所以，以AB為直徑的圓經過y軸上的定點(0,1)和(0,-3).

評注：曲線過定點問題常見解法有兩種，一是通過特殊位置確定定點再證明曲線過定點；二是先求出曲線的軌跡方程，再通過曲線的軌跡方程求軌跡所經過的定點.本題解法三屬于第二種解法.

解法四：證明：如圖所示，記拋物線C的準線與y軸的交點為P，分別過點M，N作準線的垂線交準線于M′，N′，連接M′F，N′F，PA，PB，由引理得O，N′，M三點共線，且OP=OF，N′P∥AF,所以ON′=OA，所以四邊形N′PAF為平行四邊形，所以N′F∥PA，同理M′F∥PB.

由引理得M′F⊥N′F，結合等角定理得PA⊥PB,所以以AB為直徑的圓經過y軸上的定點P(0,1).根據對稱性可知以AB為直徑的圓經過y軸上的另一個定點P′(0,-3).

綜上所述，以AB為直徑的圓經過y軸上的定點(0,1)和(0,-3).

評注：解法四為純幾何證法，通過拋物線焦點弦的兩個性質，結合平面幾何的知識，可以證得結論.與解析法相比，幾何證明方法的特點體現在“巧”和“快”，避開了圓錐曲線問題的一些繁雜運算，過程簡潔干脆.

四、規律探索

本題看起來平常，但實際上背景豐富，設問新穎，有一定的區分度，是一個值得深入研究的好題.接下來通過開口向右的拋物線來闡述本題所隱藏的解析幾何的規律，并從通性通法的角度去證明這個結論.其他形式的拋物線可以通過類比得到相應的結論.

證明：設過點Q(m,0)的直線l的方程為y=k(x-m)(k≠0).

評注：2019年北京卷理科第18題就是性質二當拋物線開口向下，取n=-1,m=1,p=2時的一種特殊情況.

五、規律推廣

上述兩個結論可以推廣到橢圓和雙曲線.

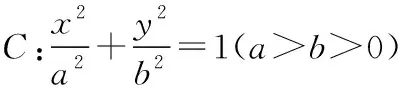
證明：設過點Q(m,0)的直線l的方程為y=k(x-m)(k≠0).

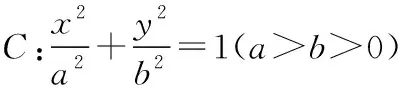
證明：設過點Q(m,0)的直線l的方程為y=k(x-m)(k≠0).

六、總結反思