怎樣培養學生的創新思維

（四川省儀隴縣第二中學 四川 南充 637600）

創新意識是指學習者主動發現問題，積極探索求解問題的思路和方法，從而充分發揮自己的潛力的一種心理取向。

教育本身就是一個創新過程，新時期下的教師必須具備培養學生創新思維的能力，改變以前全部灌輸的教學方法，以培養學生創新意識和實踐能力為目標。中學數學教學內容是前人創新的產物，數學知識源于創新，創新思維又寓于首先教學教學之中。正因為有創新思維才有一維、二維……n維空間的發現，也才能解決世界級難題（如：七橋問題）。那么，我們在數學的教學中怎樣培養學生的創新思維？下面我談談幾點看法：

1.注重培養學生的觀察能力，發展學生的創新思維

“任何思維，不認它是多么抽象的和多么理論的，都是觀察分析經驗材料開始的。”觀察是思維的前哨，是啟動思維的按扭。正如有牛頓細心的觀察才發現了萬有引力定律。觀察的深度，決定著創新思維的形成。引導學生明白對于一個問題，不要急于按想的套路求解，而要深刻地觀察、思考，這樣不但能解決問題而且還能創建性地找到解決該問題的契機。善于觀察不但能培養學生的創新思維，而且還能讓學生克服定向思維。

例如：解方程（2009-X）2+（X-2008）2=1

如果按常規解法去括號、移項、合并，難以湊效，反而計算麻煩。但是仔細觀察，分析，不難發現，2009-2008=1，則可以把方程右邊的1換成2009-2008，再添上-X+X，即：（2009-X）2+（X-2008）2=［（2009-X）+（X-2008）］2

整理：2（2009-X）（X-2008）=0

所以：X1=2009X2=2008

這樣既解決了問題，又簡化了計算過程，降低了計算的復雜性。

2.引導學生一題多解，發展學生的創新思維

在數學中教學中，注重發散思維的訓練，不緊可以開闊學生的思維而且對于培養學生勇于探索新方法、新理論。通過一題多解，引導學生從不同角度思考問題，分析問題。使學生不滿足常規方法，而求新思路、新方法。使學生解題思路開闊，妙法橫生。

如：求一次函數Y=9X-5和Y=9X+1的交點坐標。可以用圖解法，移用圖象求交點坐標，也可以利用方程組來解。不同的方法揭示出數與形的結合，又溝通了幾類知識的橫向聯系。

再如：已知（如圖1），梯形 ABCD中，AB∥CD，以 AC和 AD為邊作平行四邊形ACED，連接BE交DC于點F，求證：EF=FB。

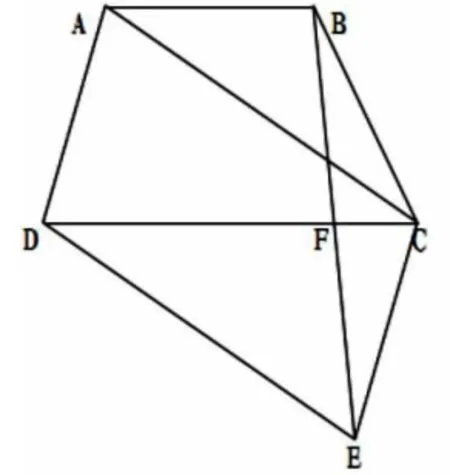
（圖1）

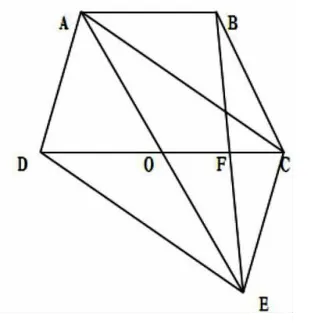
（圖2）

思路1：由題設AB∥CD，對照要證明的結論EF=FB，聯想平行線等分線段定理的推論2：經過三角形一邊中點平行于另一邊的直線平分第三邊，因此要構造一個三角形，連結AE交CD于O（如圖2），利用平行四邊形 ACED和性質AO=EO，即可證明結論。

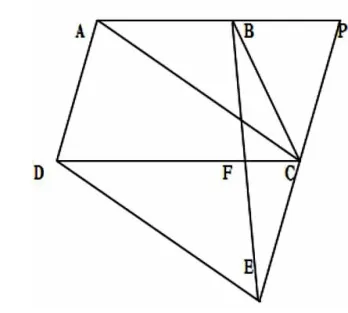
（圖3）

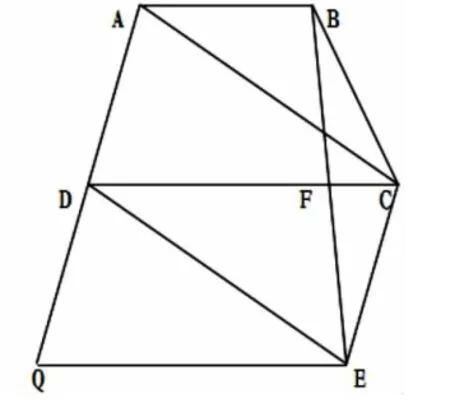
（圖4）

思路2：與思路1類同，也可延長EC交AB的延長線于點P（如圖3），構造出可以應用平行線等分線段定理推論2的△EPB，以及另一個平行四邊形APCD從而可證CP=AD=CE，從而證得。

思路3：設法構造出可應用平行線等分線段定理（或推論1）的基本圖形來證明，由AB∥CD，只要再畫第三條平行線，即過點E作EQ∥AB，交AD的延長線于點Q（如圖4），這樣由AD=CE=DQ，EQ∥AB∥DF，即可證明結論。

一題多解是命題角度的集中，解題方法的發散；多題一解是命題角度的發散，解法角度的集中，而一題多變是命題和解法的同時發散。運用上述手段要注意多種思維方式的相互滲透和相互影響，進而把它們辨證地聯系在一起，才能使學生的思維更加靈活、敏捷，以促進思維結論的完善。

3.培養學生學會質疑，發展學生的創新思維

質疑問題本身就蘊含創新思維的火花，也是創新的起點。只有善于發現問題和提出問題，才能夠在此基礎上思考和尋求解決問題的方法。有疑問才能提高，有疑問才能思考，有疑問才能進步。因此，教師在教學中要經常鼓勵學生多問幾個為什么？要大膽提出問題，帶著問題去思考，去探索，去研究。

4.協作學習、自主學習，發展學生創新思維

獨創性，是創新思維的本質特點，獨具一格。在教學過程中要注重培養學生的獨特性和自主性，引導學生質疑、調查、探究，在實踐中學習，促進學生在教師指導下主動地、富有個性地學習。

協作學習是指通過兩個或兩個以上的個體在一起，從事學習活動，互促學習，以提高學習成效的一種學習形式。它以建構主義理論和人本主義學習理論為基礎。協作學習，一方面培養了學生的學習興趣，激發了學生的學習主動性；另一方面也便于學生按照自己的情況安排學習內容和進度，鍛煉了學生的自學能力，培養了良好的學習習慣和團結協作精神。

對于學生的思維能力，特別是創新思維能力的培養，是一個很復雜而系統的領域，這需要我們老師在教學中不斷探索、總結，再探索、再總結才能取得很好的效果。在思維和解題中要做到有“法”可循、有“路”可行，有“據”可依。但有些學生往往忽視知識的靈活運用，受到某些方法的局限，形成一定的思維定勢，影響了思維的靈活性，因而我們教師在教學中應設法克服學生的某些思維定勢，注重多角度思維，培養學生思維的靈活性和全面性。

總之，要把數學的創新思維能力的培養貫穿于整個數學教學中，才能培養出有用之才。教學實踐中，學生創造思維的培養是多方位的，既需要教師的因勢利導，也需要學生的積極思考與配合，只有師生共同努力，才能教學相益，才能更好的培養學生的創新思維能力。