載體初始姿態對單軸旋轉慣導誤差傳播的影響*

徐志浩，周召發，郭 琦，徐梓皓，常振軍

(1 火箭軍工程大學兵器發射理論與技術國家重點學科實驗室， 西安 710025； 2 96902部隊， 北京 100000)

0 引言

1 單軸旋轉慣導系統誤差方程

1.1 姿態誤差方程

旋轉調制型捷聯慣導系統姿態誤差方程為：

(1)

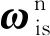
(2)

式中：s系為IMU坐標系，εs、δKg、δG分別為陀螺常值漂移、標度因數誤差矩陣和安裝誤差矩陣。

1.2 速度誤差方程

旋轉調制型捷聯慣導系統速度誤差方程為：

(3)

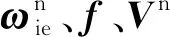
(4)

式中：▽s、δKa和δA分別為加速度計零偏、標度因數誤差矩陣和安裝誤差矩陣。

1.3 位置誤差方程

(5)

式中：VE、VN、VU分別為載體在導航系下東北天方向速度，δVE、δVN、δVU分別為載體在導航系下東北天方向速度誤差，L、λ、h分別為載體所在點的緯度、經度和高程，RM、RN分別為子午圈和卯酉圈的曲率半徑。

2 旋轉調制的自補償原理

2.1 靜基座條件下的系統誤差傳播方程

因為純慣導解算的高度通道是發散的，故在分析系統誤差特征方程時不考慮δVU和δh。根據式(1)、式(3)和式(5)得，靜基座條件下的系統誤差方程為[8]：

(6)

由式(6)可知，由于經度誤差δλ并沒有以輸入量的形式出現在其他系統誤差方程中，即經度誤差在系統回路之外，對系統的動態特性不產生影響，故在建立誤差特征方程時暫不考慮δλ。

忽略經度誤差δλ后，將式(6)的前6個方程改寫為矩陣形式：

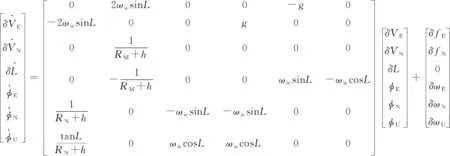
(7)

為了便于分析，下面將地球近似為球體并忽略高程h，即設RM=RN=R。將式(7)簡記為：

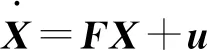
(8)

對式(8)進行拉普拉斯變換，得到靜基座條件下的誤差傳播方程為：

(9)

式中：N(s)為系統特征矩陣(sI-F)的伴隨矩陣；Δ(s)為系統特征方程。

(10)

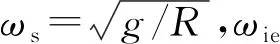
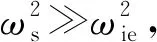
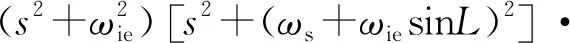
[s2+(ωs-ωiesinL)2]

(11)

求解式(11)，得系統的特征根為：

(12)

對式(9)作拉普拉斯反變換，可得到式(6)中前6個狀態量的解析解，因經度誤差δλ不在式(7)中，需要單獨計算。由式(6)可知:

(13)

對式(13)進行拉普拉斯變換得：

(14)

代入δVE(s)，作拉普拉斯反變換，即可得到經度誤差δλ的解析解。

忽略解析表達式中的振蕩項，保留常值項和積累項，可以得到慣性器件等效常值誤差與系統誤差的函數關系為：

(15)

2.2 陀螺常值漂移的自補償原理

設初始時刻IMU坐標系與載體坐標系重合， IMU繞豎直方向以恒定的角速度ω開始轉動，則t時刻IMU坐標系與導航坐標系關系為[9]:

(16)

僅考慮常值漂移時，由式(16)得:

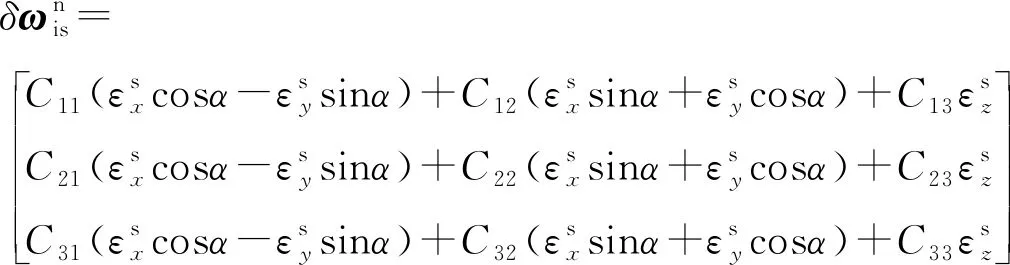
(17)

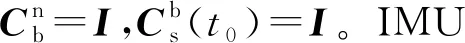
(18)

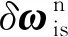
(19)

2.3 載體初始姿態對等效陀螺常值漂移的影響

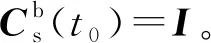
當IMU以角速度ωc繞zs軸連續旋轉時，直接對式(17)整周期積分得:

(20)

由于姿態矩陣是單位正交陣:

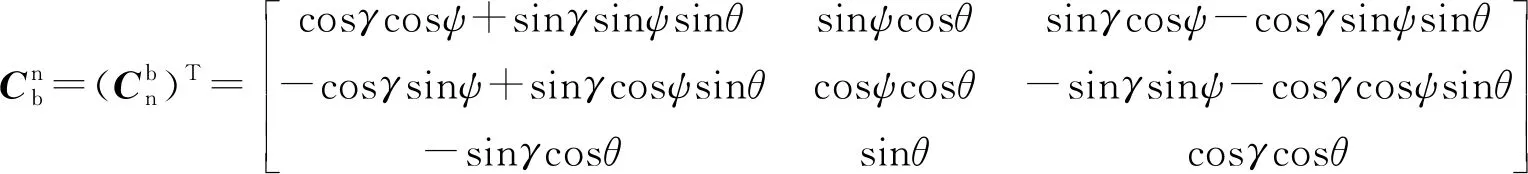
(21)

將式(21)代入式(20)得：

(22)

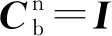
3 仿真試驗與分析

為了直觀反映旋轉調制過程的自補償效果，以單軸連續旋轉方案為背景設計仿真試驗。從式(6)系統誤差模型出發，進行符號表達式的拉氏變換和反變換。而后，將參數值代入拉氏反變換后的公式，得到對應圖像，以使得理論推導的解析表達式(15)與MATLAB符號運算的圖像相互印證。

3.1 載體系與導航系重合時的誤差傳播仿真

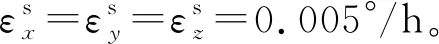
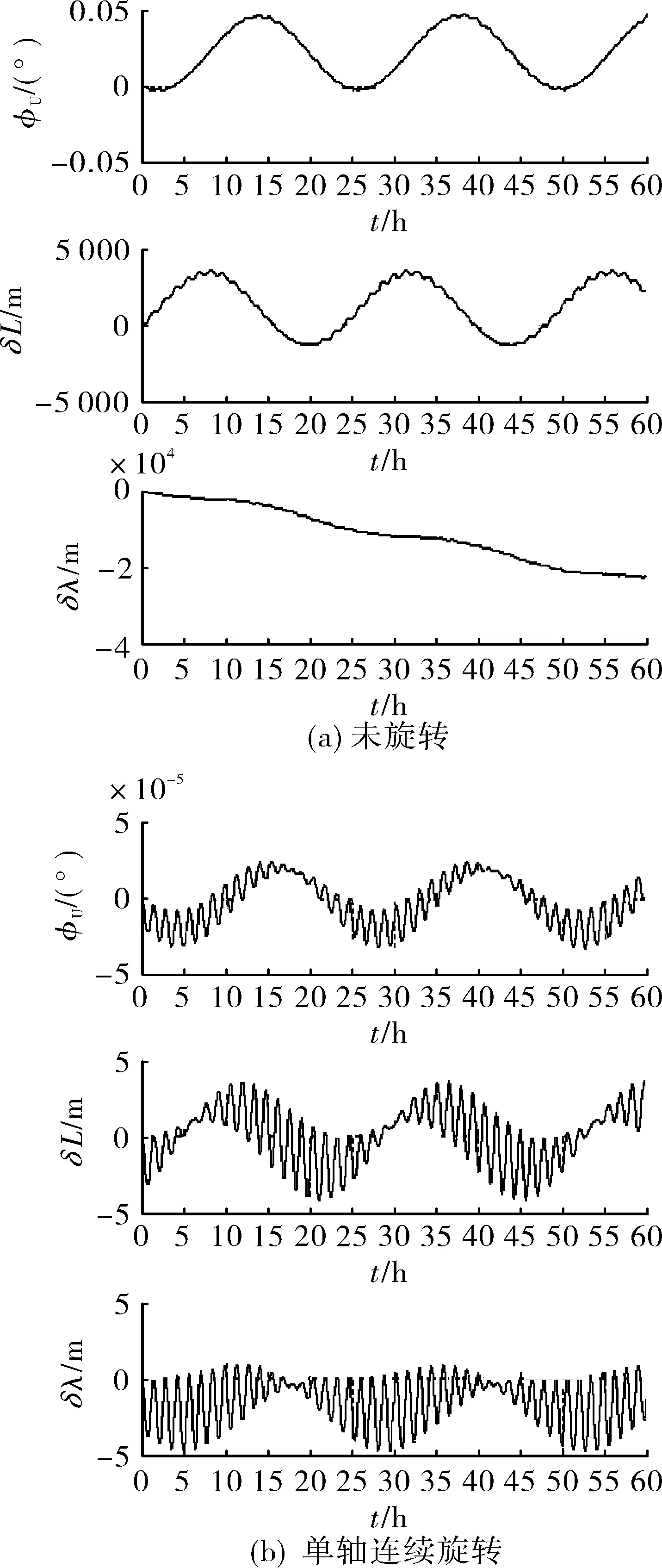
圖1 x,y軸陀螺漂移引起的導航誤差對比圖

如圖1所示，未旋轉調制時，陀螺常值漂移除了引起周期振蕩傳播的誤差外，還產生航向角和緯度的常值誤差，更嚴重的是產生隨時間積累的經度誤差。單軸連續旋轉將與旋轉軸垂直平面內的陀螺常值漂移調制成周期變化的量，經過積分后在水平面內的作用結果為零，使導航誤差明顯減小。仿真結果與理論分析一致。

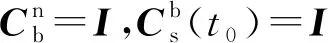
(23)

(24)

3.2 載體系與導航系任意姿態時的誤差傳播仿真

如圖2所示，當橫滾角γ=0°且俯仰角θ=0°時，航向角ψ的取值對zs軸陀螺漂移引起的導航誤差沒有影響，與前述理論分析一致。

將θ=10°,γ=10°,ψ=270°代入式(22)得:

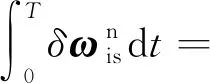
(25)

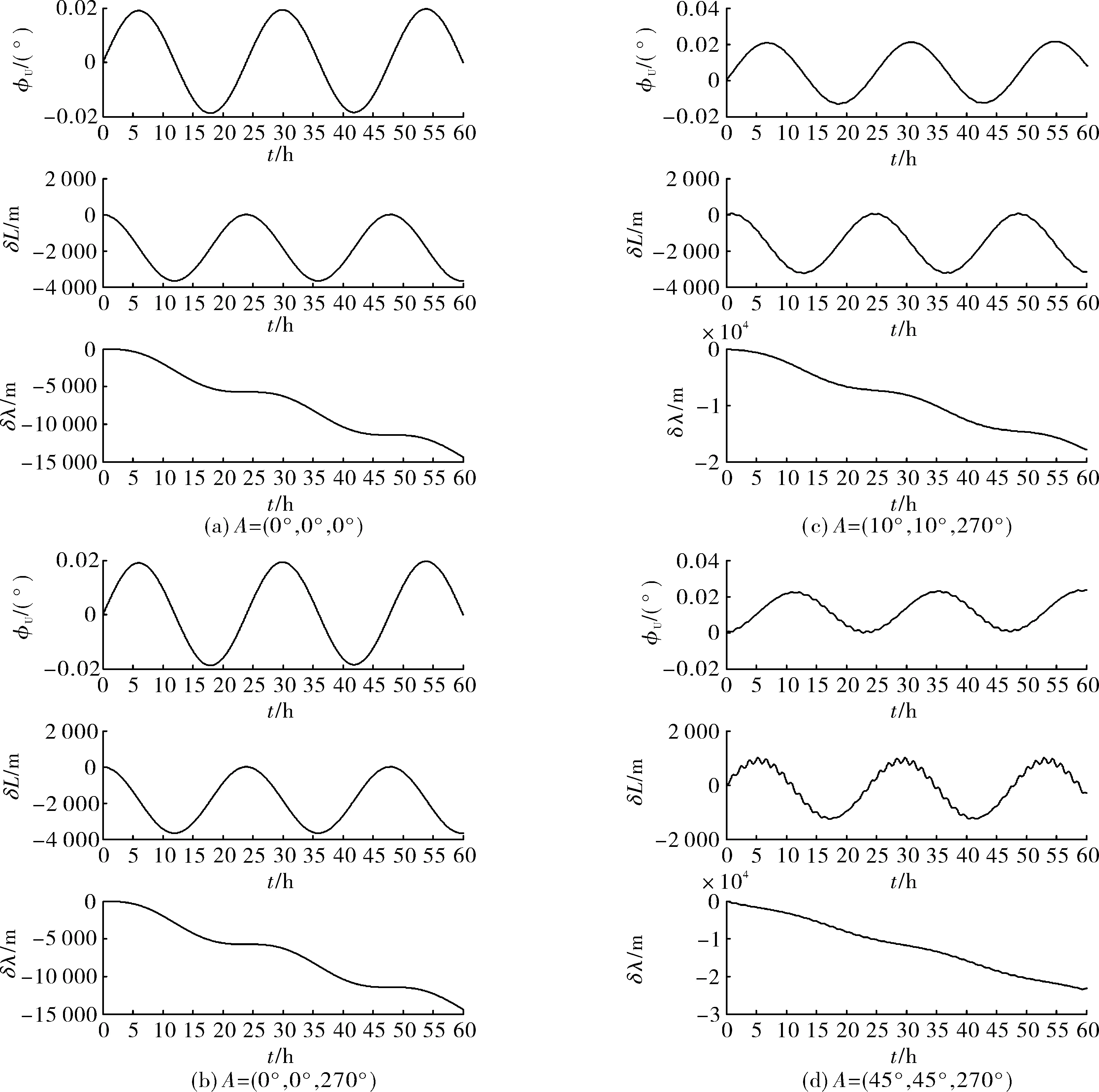
圖2 不同初始姿態時z軸陀螺漂移引起的導航誤差對比

將θ=45°,γ=45°,ψ=270°代入式(22)得:

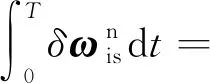
(26)

對比式(25)和式(26)，與圖2(c)相比，圖2(d)δωN較大，引起式(15)中與δωN相關的航向失準角φU的常值項增大，故圖2(d)φU的曲線均值略大于圖2(c)φU。由于θ=45°,γ=45°,ψ=270°時δωN較大且δωU較小，代入式(15)中可得緯度誤差δL的常值項數值增大，因此圖2(d)δL的曲線均值較圖2(c)明顯上移。

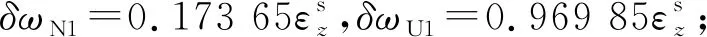
因此，相同時間內圖2(d)δλ的積累項誤差大于圖2(c)。仿真結果與理論分析一致。

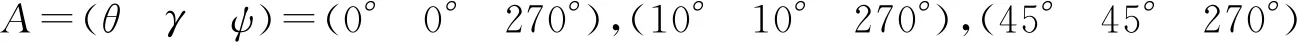
根據式(15)可知影響航向角精度的主要因素是δωE。對于實際的單軸旋轉慣導系統，絕大多數的初始對準環境為ψ≠0。雖然使δωE=0的θ、γ組合有多種，但在ψ的真值未知或存在誤差時，θ、γ除(0,0)外的其他解不能準確求出。為了實現旋轉調制效果的最優且簡化操作流程，應將載體調至水平即θ=0,γ=0，只需要一個水準器即可。室外進行車載初始對準時，若難以準確調平，也應盡量選擇較平整的地勢。

4 結論

基于旋轉調制型捷聯慣導系統的誤差模型，推導了靜基座條件下的捷聯慣導系統誤差傳播方程，得到了慣性器件等效常值誤差與系統誤差的函數關系，分析了單軸連續旋轉時陀螺常值漂移的調制形式及其對系統誤差的影響，對任意載體姿態下陀螺常值漂移的誤差傳播特性進行了仿真并得出結論：載體調至水平狀態時旋轉調制效果最優。