圓錐運動下幾種姿態算法的比較與誤差建模*

熊麗娟，朱洪濤，王志勇，曹娟華，周 波

(1 南昌大學機電工程學院， 南昌 330031； 2 南昌航空大學航空制造工程學院， 南昌 330063；3 南昌航空大學測試與光電工程學院， 南昌 330063)

0 引言

實時姿態解算是導航、機器人、遠程操作和虛擬現實等工程領域的重要技術之一[1-4]。計算機和傳感器的飛速發展對姿態精度和計算速度提出了更高的要求。此兩者不僅和傳感器性能有關，還和處理器所采用的姿態算法緊密相關。評判選擇姿態算法時，常須考慮其在最不利條件下的性能。圓錐運動因可能引起最大不可交換誤差[5-6]，被眾多文獻認定為最不利條件。但常用姿態算法在不同圓錐運動條件下的性能表現尚未得到系統研究。

姿態解算方法中，四元數法因其非奇異性、簡單性和計算時間短等優點而成為目前最流行的方法[7-9]。 文中針對4種基于四元數的常用高精度姿態算法，研究它們在不同圓錐運動條件下的姿態解算性能。這4種算法分別為：四子樣旋轉矢量算法(RV4)，四階龍格庫塔算法(RK4)，四階泰勒算法(T4)和五階泰勒算法(T5)。為進行較全面的分析，文中通過變化錐進步長和錐半角進行了一系列圓錐運動仿真實驗。實驗以姿態角誤差，即偏航、俯仰和橫滾角3者的誤差作為結果輸出，籍此研究4種算法的姿態解算精度，并歸納建立4者的姿態角誤差模型。相較而言，前人文獻更傾向于依據誤差漂移參數[1]、旋轉矢量幅值誤差或姿態四元數誤差[5, 7, 10]來評價姿態算法的精度。這類誤差模型因推算過程有假設與簡化存在，并不準確，亦不利于理解和用作誤差補償。

所選4種算法雖非當前精度最高的姿態算法[11-13]，但因文中意在展示一種新的姿態算法研究方式，故并不需要遍歷各種高級算法。另，因篇幅有限，文中僅展示了實驗結果中有代表性的一部分。

1 姿態解算數學模型

姿態解算需先更新姿態四元數，再將其換算為姿態角，即橫滾角、俯仰角和偏航角。除旋轉矢量法外，姿態四元數的更新一般以式(1)為基礎：

(1)

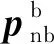
(2)

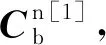
(3)

θ=-arcsinc31

(4)

式(4)中atan2是C++中的函數，返回-π ～ π范圍的弧角。當θ= ±π/2時，由于橫滾軸和偏航軸已成平行軸[1]，故無法獲取φ和ψ的唯一解。因此，當θ接近±π/2時，可采取交替更新φ和ψ的方法[1]。

2 圓錐運動下的四元數更新算法

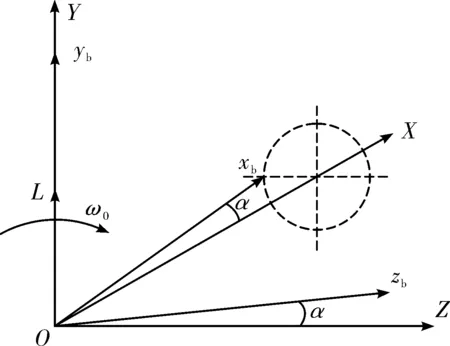
圖1 典型圓錐運動示意圖

典型圓錐運動是因系統兩個正交軸上同時被施以相位差90°的角振動而產生[1]，具體如圖1所示：O-XYZ為導航坐標系，O-xbybzb為載體坐標系；OL是從導航到載體坐標系的旋轉矢量，正在YOZ平面內以恒角速度ω0旋轉，載體坐標系此時即作典型圓錐運動，其xb軸可看作在導航坐標系空間中一錐半角為α的圓錐面上滾動，OL幅值亦為α。將OL記為Φ：

(5)

式中：t為載體圓錐運動時間；文中仿真的載體零點狀態如圖1所示。Φ的等效姿態四元數為：

(6)

載體相對導航坐標系的角速度為：

(7)

根據式(6)，不同時刻的精確姿態角可以算得；而式(7)可作為角速度傳感器測得的轉速，實現圓錐運動仿真。

2.1 RV4算法

在姿態更新區間Δt內，載體從(k-1)Δt到kΔt時刻的四子樣旋轉矢量μk計算如式(8)[7]。

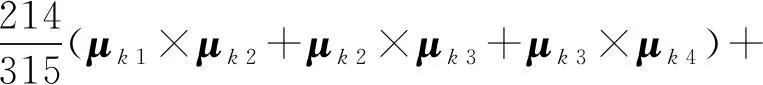
(8)

式中：k=1,2,3,…；μk1、μk2、μk3、μk4分別對應四分之一更新區間內的角積分。對典型圓錐運動而言，μki(i=1，2，3，4)可通過對式(7)積分得到。

求出對應旋轉矢量μk的四元數為：

(9)

式中：μk為μk的幅值。

(10)

2.2 RK4算法

典型圓錐運動下，姿態四元數傳播方程具體化為：

(11)

qk=qk-1+(K1+2K2+2K3+K4)Δt/6

(12)

式中：K1、K2、K3、K4按式(13)順序求解：

(13)

2.3 泰勒級數算法

使用泰勒級數法[14]求解方程(11)得：

(14)

式中：上標(j)代表求導階數，l為所使用泰勒級數法的階數。

3 實驗結果

3.1 基礎分析

文中變化錐進步長(即ω0Δt，簡記為β)和錐半角α進行了一系列圓錐運動仿真實驗。為方便起見，文中所有仿真中ω0均保持在30°/s，而Δt在0.1 ～ 4 s間變化，這樣錐進步長β在3°～ 120°間變化；錐半角α在5°～ 85°間變化。

當α=5°、β=3°時，4種算法的姿態角誤差如圖2所示。此時4者精度由高到低排序為：RV4、T5、RK4、T4。圖2還顯示，由于圓錐運動中姿態角的周期變化，所有姿態角誤差都以類諧波的形式隨時間波動。

圖2中120 s的仿真誤差發展趨勢不夠明朗，因此仿真時長被延至20 000 s，其實驗結果(未圖示)清楚表明各算法的姿態角誤差絕對峰值幾乎均隨時間線性增加，且橫滾角誤差發散速度基本都比偏航和俯仰角誤差發散速度快。這與文獻中所述“圓錐誤差(漂

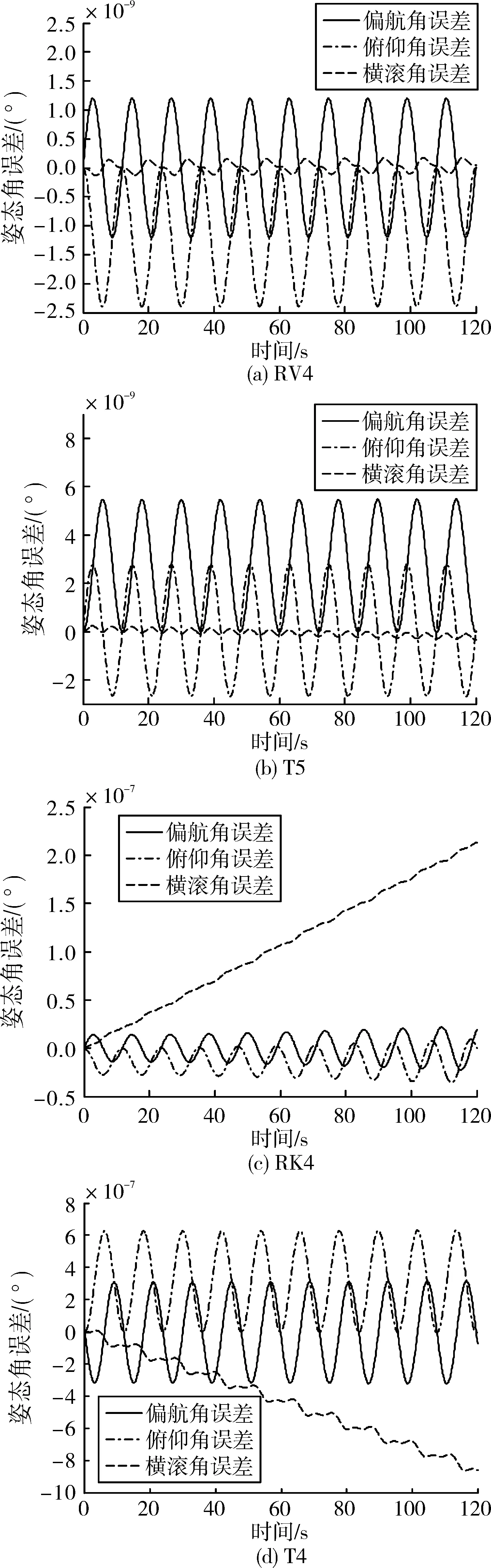
圖2 120 s仿真中的姿態角誤差(α=5°、ω0=30°/s、Δt=0.1 s)

移)主要出現在錐進軸上”[7, 15-16]相吻合。雖然多數文獻根據其簡化誤差模型認為偏航和俯仰角誤差基本無漂移[7, 15-16]，但仿真實驗結果證明，這兩者的絕對峰值其實也在累加(漂移)，只是速度通常沒有橫滾角誤差發散得快。

3.2 誤差建模

為研究姿態誤差會如何隨步長或其它因素的變化而變化問題，文中將4種算法在120 s仿真時間內的最大姿態誤差，即最大姿態角絕對誤差E繪于圖3、圖4之中。圖3描繪了E在不同錐進步長下如何隨錐半角α的變化而變化，圖4則描繪E在不同錐半角下如何隨錐進步長β的變化而變化。

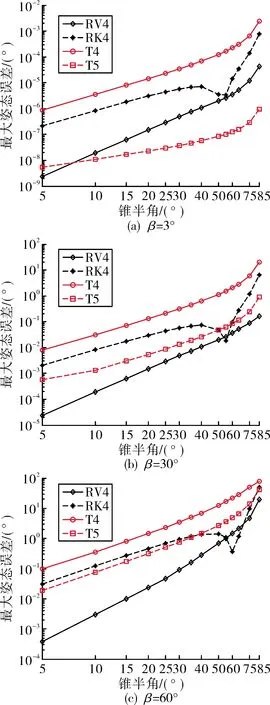
圖3 120 s仿真中最大姿態誤差與錐半角的關系

圖3、圖4均反映出RV4、T5、RK4和T4這4者的精度排序并不總是不變的,比如，T4算法雖不如RV4和RK4精確，但并非總是不如T5；T5算法在錐進步長較小時精度較高，但隨著錐進步長增大，其精度相比其余3者急速下降——也就是說，T5的精度易受步長影響；而最易受錐半角變化影響的是RV4算法，某些時候它的精度還不如RK4。

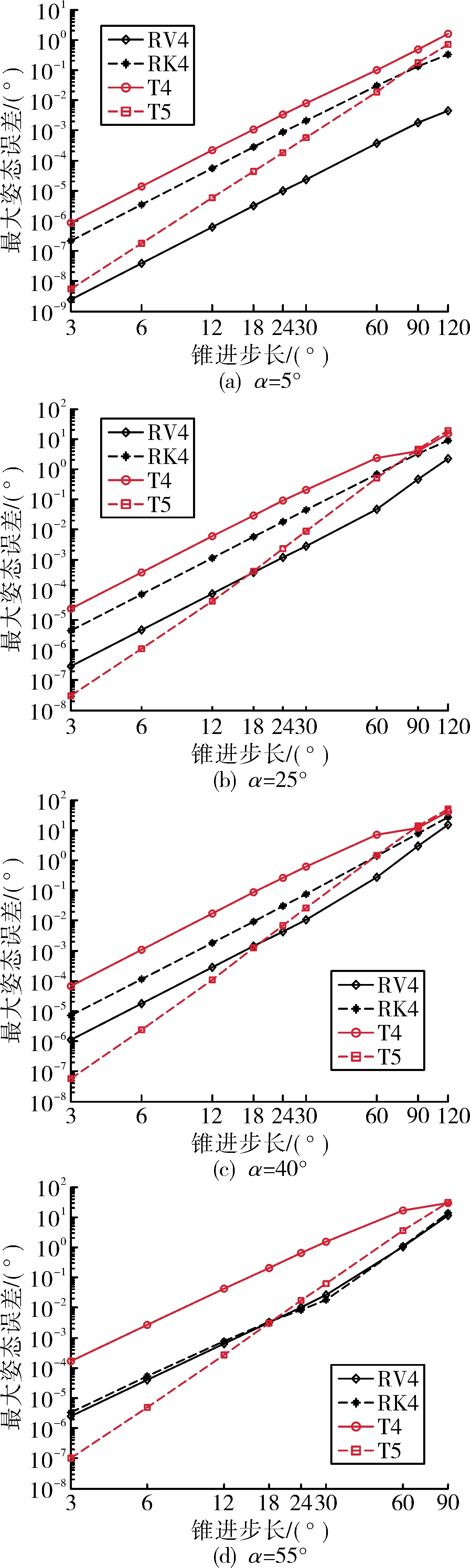
圖4 120 s仿真中最大姿態誤差與錐進步長的關系

由圖3可知，當α不超過30°時，lgE與lgα間基本呈線性關系。由圖4可知，當β不超過30°時，lgE與lgβ間亦基本呈線性關系。為此，可用式(15)表達4種算法的E與α、β之間的關系。

E=Aαmβn

(15)

式中：上標m即圖3數據擬合線斜率，上標n即圖4數據擬合線斜率，系數A取決于運動時長t和錐進速度ω0。對不同的算法，這3個參數自然不同。

根據上一小節中的分析，A值基本與時間t成正比，也與ω0成正比，故將式(15)中的A代以Cω0t，得：

E=Cω0tαmβn

(16)

式中:C是取決于算法的常數。

為確定4種算法的m和n值，將圖3、圖4中橫坐標不超過30°的數據擬合直線，斜率m、n分別列于表1、表2中。

表1 不同錐進步長β下的m值

*使用部分數據擬合。

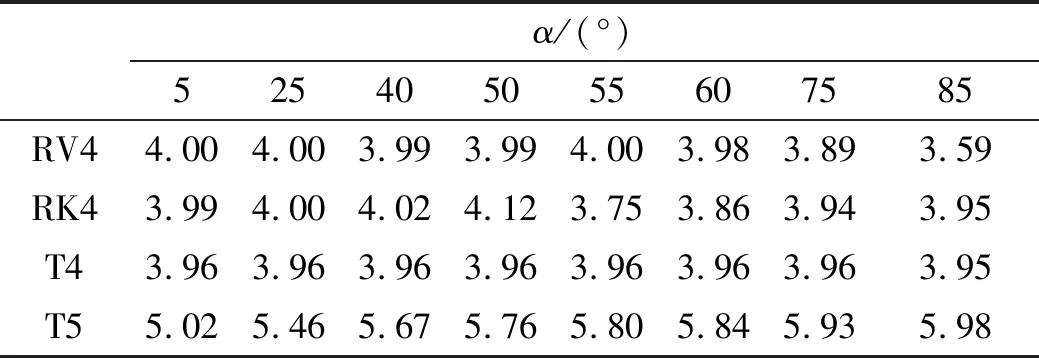
表2 不同錐半角α下的n值

表1顯示：當β≤ 60°，RV4算法的m總在3左右；當β≥ 90°時，其m在4左右。深入剖析發現，β≤ 60°時，120 s仿真時間內RV4算法的最大姿態誤差E為俯仰角誤差；而β≥ 90°時，其E為橫滾角誤差。所以，m值從3跳變到4是因為E從俯仰角誤差切換到了橫滾角誤差，或者說3是RV4俯仰角誤差的m值，而4是RV4橫滾角誤差的m值。

須申明的是，當運動時間足夠長，橫滾角誤差通常將成為3個姿態角誤差中最大的，此時E即橫滾角絕對誤差極值。

表1還顯示：①無論β如何變化，RK4和T4算法的m值均在2左右。因為在這兩種算法的120 s仿真實驗中，大多數情況E都是橫滾角誤差，所以其m值未出現跳變。②當β= 3°，T5算法的m在1左右；當β≥ 12°，其m在2左右。經剖析發現，1實為T5偏航角誤差的m值，而2為其橫滾角誤差的m值。

同理由表2推知：①當α不超過75°，RV4橫滾角誤差的n總在4左右；②無論α如何變化，RK4橫滾角誤差的n總在4左右，T4橫滾角誤差的n亦在4左右，而T5橫滾角誤差的n總在6左右。

值得一提的是，表2中RK4算法的n值在α= 55°時突然降至3.75。這種突變在圖3中也有出現——RK4的E值在α= 55°附近突然下降。圖4則反映，當α從5°升至55°，RK4的精度從遠不如RV4漸升至與其相當。經深入分析，這一現象源自RK4橫滾角誤差發散方向會隨α增加而變化——當α升至一定值，其誤差發散由朝正方向發展變為朝負方向發展。該轉變點α值會隨β值變化，β增大，轉變點α值也漸漸增大；當β增至120°時，轉變點消失(因為α不會超過90°)。橫滾角誤差發散方向的改變令RK4橫滾角誤差在轉變點處大大減小并散失其誤差支配地位。上述現象在4種算法中為RK4算法所獨有，一定程度上提高了RK4算法對高機動運動環境的適應能力。這也是為什么一些學者會發現RV4的抗干擾能力不如RK4[17-18]。

綜上，當α≤ 30° 且β≤ 30°時，圓錐運動t時長內以上4種算法的最大橫滾角誤差，記為|δφ|max，可建模如下：

(17)

式中：|δφ|max單位(°)，錐進速度ω0單位(°)/s，圓錐運動時長t單位s，錐半角α和錐進步長β單位(°)；利用實驗結果算得系數C1、C2、C3、C4依次為：9.11e-19，2.63e-14，1.20e-13，5.31e-18。該式給出的是錐進軸姿態角誤差模型，而非以往文獻常給出的“圓錐誤差模型[7]”(即文中旋轉矢量μk的誤差幅值模型)。

在同樣使用環境下用4種算法分別進行1 200次姿態更新發現：RV4算法用時0.168 8 s， RK4算法用時0.270 7 s，T4算法用時448.049 6 s，T5算法用時1 365.3 s。顯然，RV4是4者中計算速度最快的算法，而T5是四者中速度最慢的算法。

4 結論

文中研究了4種高精度姿態算法，通過分析其在圓錐運動下的姿態角計算誤差，發現其精度排序將隨條件的改變而變化。這和以往一些文獻給出的精度優劣論斷不一樣[19-20]。

就計算速度而言，RV4和RK4算法比T4和T5算法快得多。綜合考慮計算精度和速度，多數情況下RV4算法會是4者中姿態解算性能最佳者。

文中還建立了4種算法的錐進軸姿態角誤差模型，亦即文中實驗條件下的橫滾角誤差模型。在工程應用中，若能即時對待測物的角速度進行頻域分析，可針對其包含的圓錐運動分量使用此誤差模型進行誤差預測乃至補償[21-22]。