水下低頻球面聲波近場與遠場散射特性研究

張 健，周奇鄭，王德石

(海軍工程大學 兵器工程學院，湖北 武漢，430033)

0 引言

低頻聲波水下傳播距離遠，是遠距離探測敵方目標的主被動聲吶設備采用的重要能量形式。由于低頻聲波的波長不比目標特征尺寸小，致使目標表面聲壓和振速的比值不能近似為平面波的形式，采用傳統的射線法或數值計算方法都存在較大偏差。因此，研究水下低頻聲波散射聲壓的統一漸近解，獲得其散射機理，在水下聲散射理論、水聲測量等方面，具有重要理論和應用價值。

低頻聲波的散射機理是水聲學研究中的基礎性問題。聲波在水下傳播時遇到比其波長小的障礙物時會產生散射，即Rayleigh 散射。以往關于Rayleigh 散射的研究主要是針對平面入射聲波[1-4]，然而采用平面聲波假設計算低頻散射聲波與實際測量結果總有一定的偏差，因此，研究非平面聲波的散射機理具有重要意義。聲散射主要研究的是聲波遇到目標即障礙物時的散射聲場，只要目標表面和聲傳播介質的聲學特性不同就會產生散射。嚴格的理論解法主要有積分方程法和分離變量法。對于散射問題，受聲波激勵作用的散射表面就像次級聲源一樣發出散射波，積分方程法是以Helmholtz 和Kirchhoff 對Huygens 原理的數學解釋為基礎，通過引入符合波動方程的Green 函數并根據Gauss 公式將包含哈密頓算子的體積分轉化為曲面積分，從而通過被積曲面上的表面聲壓和法向振速求得目標的散射聲場[5-6]。原則上積分方程法的解是精確的，可以應用于任意復雜形狀的目標，但在具體運用時，積分方程需要用數值方法求解，又變成了一種近似方法，并且在實際計算中會出現解的唯一性和奇異積分等問題。

分離變量法本質上是將入射聲場和散射聲場按照某種坐標系下完備正交函數族的級數展開[7-8]，比如基本波函數的Rayleigh 簡正級數，再根據邊界條件以及函數的完備正交性求得散射聲場的系數，最終得到散射聲場的級數解。利用簡正級數解可以得到目標的各種散射特性，如頻率響應特性、方向特性等。對于球殼和圓柱殼等典型殼體，在入射平面聲波激勵下的散射問題已得到詳細研究，文獻[9]和[10]給出了平面波從球形和無限長圓柱形散射聲壓的無窮級數表達式。Rayleigh 在1872 年就給出了單頻球面聲波遇到球形障礙物散射問題的精確解，該解是由球Bessel 函數和Legendre 多項式相乘組成的無窮級數的疊加，不容易用于揭示散射的物理機理。近年來，Godin 等[11-12]采用級數展開的形式，研究了低頻球面聲波的散射問題，其研究工作距工程應用還有一定的差距。

由于可以采用分離變量法獲得典型殼體聲散射問題的簡正級數解，且低頻球面波是較簡單的非平面波，因此，文中重點考慮低頻球面聲波遇到球形障礙物的散射問題，推導其近場和遠場散射聲壓的統一漸近解，研究漸近解的適用性、球面波散射和平面波散射的差異以及低頻球面聲波的近場和遠場散射特性。

1 低頻球面聲波散射問題無窮級數解

在水下，潛艇和魚雷頭部的橢圓結構都可近似視為球形障礙物。假定聲波頻率為ω、球形障礙物的半徑為a、球形障礙物浸沒在聲速為c、密度為ρ的均勻流體介質中。以球形障礙物的中心為坐標原點，建立如圖1 所示的球坐標系(r，θ，φ)。圖中，O為障礙物的中心、b為聲源位置、r(x，y，z)為空間任一接收點的位置，笛卡爾坐標系與球坐標系之間的轉換關系為x=rsinθcosφ，y=rsinθsinφ，z=rcosθ。

圖1 球面散射問題幾何模型Fig.1 The geometry model of spherical scattering problem

假定入射球面波的表達式為

2 散射聲壓漸近解

由于低頻聲波波長較長，水下傳播時介質對低頻聲能的吸收較少，能夠傳播的距離較遠，因此，需重點研究低頻聲波的近場和遠場特性。低頻聲波在水下傳播時遇到尺寸比其波長小的障礙物時會發生Rayleigh 散射，因此，這里主要考慮Rayleigh 散射的情形，即假定

在該條件下，式(4)中的求和級數可以在一定精度要求下進行簡化。

根據Rayleigh 公式，可以將球Bessel 函數和第1 類球Hankel 函數表示為冪級數的形式，即

由式(15)、式(16)和式(18)可以看出，當n≥2時，3 種障礙Rayleigh 散射波的級數中系數An是(ka)5高階小量；系數An都與頻率k相關，且隨n的增大迅速減小，而n≤1 的情況卻有所不同。對于軟球、阻抗球、剛性球，n=0 時，系數A0分別與ka、(ka)2、(ka)3成正比；n=1 時，系數A1與(ka)3成正比。因此，當ka＜＜1 時，散射聲波的無窮級數解可以取前3 項近似。

為了便于分析，忽略(ka)5的高階小量，可以將3 種散射情形下，n≥2 時的系數An可以統一用A1近似表示為

式中，γ=0 和1 分別對應于軟球和剛性球。

2.1 近場散射聲壓漸近解

考慮近場條件下聲波的散射問題，即接收點和聲源點都距散射體較近，有

該條件意味著： Hankel 函數可以用式(12)和式(13)表示。那么，系數An用式(19)表示，則散射聲壓可表示為

由式(21)可知，3 類邊界條件下散射聲壓的不同主要體現在包含系數A0和A1的項上，而n≥1的級數可以采用統一的形式表示。A0和A1僅與入射聲波的頻率、散射體的半徑a、以及散射體的特征阻抗參數γ有關。定義S（α，β，γ）為

式中：β=cosθ；α=a2/br；故 -1 ≤β≤1，近場條件下，0＜α＜ 1。函數S（α，β，γ）與入射聲波的頻率無關，且式(22)中沒有大的或小的參數，不能采用近似計算方法，需要給出精確的計算結果。

對于軟球體，有γ=0，根據Legendre 函數的性質[13]有

略去高階小量，將S（α，β，γ）的表達式代入散射聲壓式(21)，可得低頻近場散射聲壓的近似表達式

近場散射聲壓可以表示為位于散射體中心的單極子聲源、散射體中心與(0，0，a2/b)之間分布的偶極子源的疊加。

2.2 遠場散射聲壓漸近解

考慮遠場條件下聲波的散射問題，即接收點或聲源點距散射體中心的距離較遠，有

這時不要求式(20)成立。在式(8)和式(29)成立的條件下，由于式(15)、(16)和(18)中的系數An隨n的增大迅速降低，不需要采用聲壓的衰減進行補償，聲壓表達式(4)中的級數收斂很快，因此，在一定精度范圍內可以采用前2 階近似表示散射聲壓，球Hankel 函數采用式(13)的形式，那么遠場散射聲壓可近似表示為

2.3 散射聲壓統一漸近解

通過上述分析發現，在Rayleigh 散射區，散射聲壓都可以表示為點聲源和偶極子聲源的疊加，只是要求的條件有所不同，如果能夠在重疊區找到一個統一的公式表示散射聲壓將很有意義。

那么，散射體外的總聲壓可近似表達為

將A0代入式(33)可知，障礙物的存在一定程度上降低了散射聲壓的幅值。

3 散射特性分析

采用推導的散射聲壓統一漸近解研究低頻聲波的近場和遠場散射特性。

3.1 球面波散射聲壓的級數解與漸近解

研究球面波散射問題的精確級數解式(4)和統一漸近解式(31)之間的關系。圖2 為ka=0.1，kb=0.8，kr=0.6 時，0≤θ≤2π 范圍內，3 種邊界條件下散射聲壓的實部與虛部。

圖2 0≤θ≤2π 范圍內3 種邊界條件下散射聲壓Fig.2 The scattering acoustic pressure under three boundary conditions in the range of 0≤θ≤2π

由圖2 可知，3 種邊界條件下，在0≤θ≤2π范圍內推導的統一漸近解和球面波散射的級數解一致性較好；軟球體情形下散射聲壓的實部和虛部在θ=0 和2π 時最小，在θ=π 時最大，且關于θ=π對稱，聲壓虛部的幅值比實部的幅值大；而剛性球體和阻抗球情形與軟球體的情形相反，散射聲壓的實部和虛部在θ=π 時最小，也關于θ=π 對稱，且聲壓實部與虛部幅值的數量級相同，這與式(16)和式(18)揭示的物理意義相符，即有限阻抗小球的散射聲壓與剛性球的散射聲壓僅有微小差別，可以通過相同半徑剛性球的散射聲場得到有限阻抗球的低頻散射場。

圖3 為ka=0.2，kb=0.6，θ=π/3 時，3 種邊界條件下散射聲壓rRe（psc）和rIm（psc）與kr的關系。由圖3 可知，在給定的參數條件下，0.2＜kr＜20 范圍內，統一漸近解與球面波的級數解一致性較好。圖3 也表明，測量低頻聲波的散射特性時，應選取合適的測量點，以免測量結果處于散射聲壓的最小值點，致使測量誤差較大。

圖3 kr 變化時3 種邊界條件下散射聲壓Fig.3 The scattering acoustic pressure versus kr under three boundary conditions

圖4 為a=1，b=2，r=3，θ=π/4 時，3 種邊界條件下散射聲壓的實部與虛部隨ka的變化情況。由圖可知，當ka＜0.2 時，聲壓漸近解的實部與虛部都與級數解的結果保持一致；而當ka較大時，剛性球和阻抗球散射的聲壓與級數解的結果有差異，但變化趨勢一致，且最大誤差僅為0.002，這主要與采用的假設條件和A0、A1的截取項有關。

圖4 ka 變化時3 種邊界條件下散射聲壓Fig.4 The scattering acoustic pressure versus ka under three boundary conditions

上述分析表明，當ka較小時，采用推導的散射聲壓的統一漸近解能夠較好地代替無窮級數解，且可以較清晰地揭示散射問題的物理意義。

3.2 近場與遠場散射特性分析

研究球面波和平面波入射情形下水下球形障礙物散射問題的近場與遠場特性。文獻[10]給出了平面波散射問題的求解方法，假定平面入射聲波沿-z方向傳播，將入射平面波按球面波分解為

平面波從球形障礙物的散射聲壓為

其中，bn為待定散射系數，由球形障礙物的邊界條件確定，與球面波入射情形下散射聲壓的系數一致。

定義回聲強度為[10]

采用球面波入射情形下的統一漸近解式(32)、平面波入射情形下的無窮級數解式(35)和回聲強度式(36)研究低頻聲波的散射特性。

聲源點b距障礙物較近(kb=0.4)的情形： 圖5為ka=0.15，kr=0.6 時，3 種邊界條件下的回聲強度；圖6 為ka=0.15，kr=70 時，3 種邊界條件下的回聲強度。

圖5 ka =0.15,kb =0.4,kr =0.6 時3 種邊界條件下回聲強度(單位： dB)Fig.5 The echo strengths under three boundary conditions when ka =0.15,kb =0.4,kr =0.6 (Unit： dB)

圖6 ka =0.15,kb =0.4,kr =70 時3 種邊界條件下回聲強度(單位： dB)Fig.6 The echo strengths under three boundary conditions when ka=0.15,kb =0.4,kr =70(Unit： dB)

由圖5 和圖6 可知，3 種邊界下的近場和遠場回聲強度有明顯差異： 球面波入射情形下軟球體的近場回聲強度如圖5(a)所示呈蝶形，而遠場回聲強度如圖6(a)所示近似為圓形，也即無指向性；而平面波入射情形下的近場與遠場回聲強度均為圓形，且幅值較小。球面波入射情形下，剛性球體和阻抗球的近場回聲強度在θ=π/2、θ=3π/2 附近最大，θ=π 時次大，而遠場回聲強度均為葫蘆形，只是頭尾有區別，如圖6(b)和(c)所示；而平面波入射的情形有明顯差別，剛性球體和阻抗球的近場回聲強度為橢球形，只是在θ=π/2、θ=3π/2 附近有 2 個極大值；剛性球的遠場回聲強度在θ=π/3、θ=5π/3 附近最大，θ=π 時最小，而阻抗球的遠場回聲強度在θ=2π/3、θ=4π/3 時最大，θ=0時最小。

聲源點b距障礙物較遠(kb=60)的情形： 圖7為ka=0.15，kr=3 時，3 種邊界條件下的回聲強度；圖8 為ka=0.15，kr=63 時，3 種邊界條件下的回聲強度。

圖7 ka =0.15,kb =60,kr =3 時3 種邊界條件下回聲強度(單位： dB)Fig.7 The echo strengths under three boundary conditions when ka =0.15,kb =60,kr =3(Unit： dB)

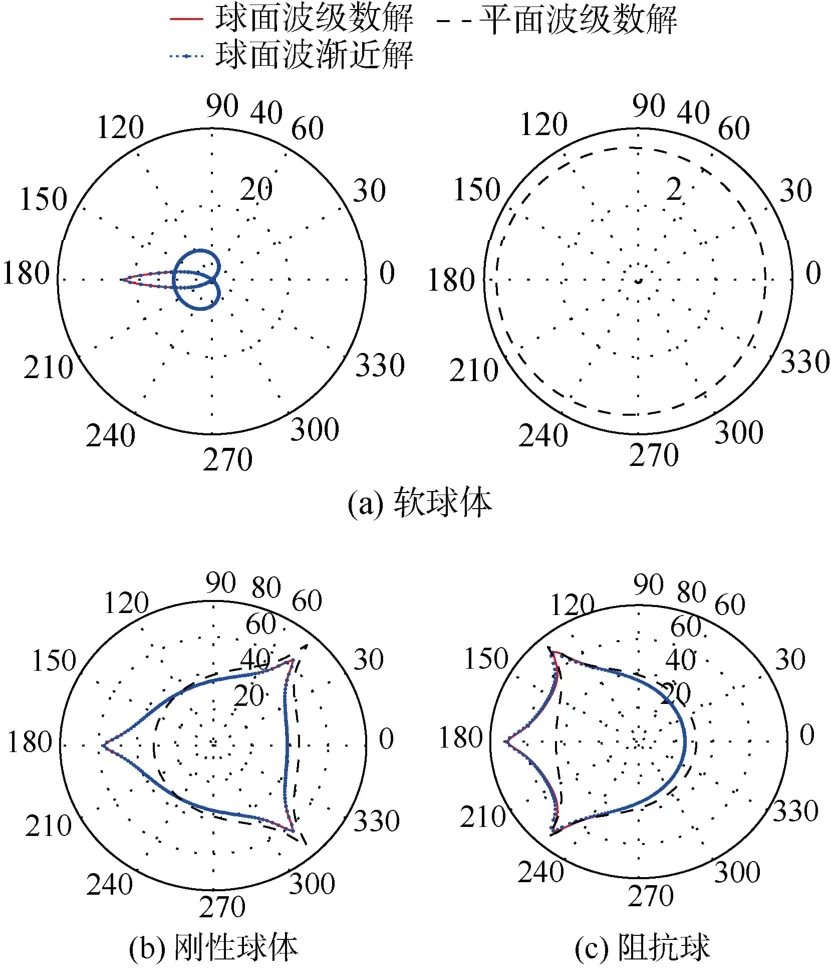
圖8 ka =0.15,kb =60,kr =63 時3 種邊界條件下回聲強度(單位： dB)Fig.8 The echo strengths under three boundary conditions when ka=0.15,kb=60,kr =63(Unit： dB)

由圖7 可知，球面入射波和平面入射波情形下，障礙物在3 種邊界的近場回聲強度基本能夠保持一致，這是主要是由于聲源距目標較遠(10倍波長左右)，聲源入射到障礙物上的球面波波陣面趨于平面，球面波入射與平面波入射基本沒有差別。由圖8 可知，球面入射波和平面入射波情形下，障礙物在3 種邊界的遠場回聲強度有明顯不同： 球面波入射情形下軟球體的回聲強度為“剪刀”形，而平面波入射情形下軟球體的回聲強度為橢圓形，且幅值較小；球面波入射情形下，剛性球體的遠場回聲強度在θ=π/3、θ=5π/3 附近最大，θ=π 時次大，阻抗球的遠場回聲強度在θ=π時最大，θ=2π/3、θ=4π/3 附近次大；平面波入射情形下，剛性球和阻抗球的回聲強度少了θ=π 處的極值點。這主要是由于接收點的散射聲壓雖然可以用平面波近似，但是接收點距聲源較近，入射聲壓不可用平面波近似。但是由于平面波散射問題的研究已較成熟，因此，下一步需要研究兩者之間的關系，以對平面波散射解進行修正，滿足球面波散射問題計算的需求。

4 結論

研究低頻聲波的散射特性對水下目標探測、低頻噪聲的抑制具有重要意義。文中針對水下低頻球面聲波的散射問題，根據3 種典型邊界條件下散射聲壓的級數解，在低頻、近場和遠場的假設條件下，采用近似形式表示 Bessel 函數和Hankel 函數，推導出了散射聲壓的統一漸近解，在此基礎上研究了低頻聲波的近場和遠場特性，研究表明：

1) 低頻球面聲波的散射聲壓可以表示為單極子聲源和偶極子源的疊加，給出的統一漸近解可以用于研究ka＜0.5 時低頻球面聲波的散射特性；

2) 聲源距障礙物較近時，不可采用平面波入射時的回聲強度代替球面波入射的回聲強度；接收點距聲源或障礙物較遠的情形下，軟球體的回聲強度為圓形，而剛性球體和阻抗球的回聲強度為葫蘆形；

3) 聲源距障礙物較遠時，在接收點距障礙物較近的情形下，可以采用平面波入射時的回聲強度代替球面波入射的回聲強度；在接收點距聲源較近的情形下，入射波的回聲強度與其形狀有關。

研究結果可用于水下低頻聲波的被動控制，可指導目標低頻探測。但文中未從理論層面給出平面波與球面波解的關系和球面波場解的精度，下一步會在理論上逐步完善，并加入低頻柱面波的研究。