彈塑性彎曲直梁的回彈變分原理及應用

陳英杰， 郭清超， 周夢飛， 張 華

(燕山大學河北省土木工程綠色建造與智能運維重點實驗室, 秦皇島 066004； 燕山大學建筑工程與力學學院, 秦皇島 066004)

關于物體變形問題的研究由來已久，而應用變分原理研究物體的變形經過了漫長的時間，經研究發現，理想彈塑性材料的耦聯系統塑性成形過程可以視為實際系統的變形，對應的反耦聯系統的變形可以作為實際系統的回彈變形。因此，可以應用反耦聯系統求解出彈塑性梁對應的回彈撓曲線方程。當前工程中涉及梁的變形及回彈問題還有很多是根據彈性理論或經驗公式解決的，存在一定的誤差，也在一定程度上造成材料浪費，為了限制彈塑性梁的變形，需要建立能夠指導實際生產應用的理論。彈塑性梁的振動問題[1-2]和彎曲問題[3-4]一直被廣大學者所關注，由于材料本構關系的原因，荷載作用下的梁會產生彎曲變形，從而截面會產生彈性區和塑性區，如何劃分彈塑性區和彈塑性梁的變形是研究熱點之一。受力構件卸載后，結構產生了反向變形，由于材料的回彈值很小，因此需要研究出有效、精確的方法解決回彈問題。中國學者對回彈問題開展了大量研究。吳斌等[5]基于U形板熱沖壓構件的殘余應力與回彈影響之間的關系進行了研究；羅之軍[6]建立了電子設備罩殼彈塑性材料有限元模型，對結構的回彈現象進行了研究；錢偉長研究發現，由于材料本構關系的原因，荷載作用下的梁會發生彎曲變形，從而會產生彈性區和塑性區，而彈性區和塑性區的分界面并不能事先給定，需要找出劃分彈塑性區的分界線；前人采用邊界待定的變分法[8-10]解決了塑性力學中理想彈塑性材料變形體彈性區和塑性區的劃分問題，以及理想彈塑性材料的梁在不同條件下的變形及回彈問題，通過求解可以得到該類問題的精確解。對彈塑性直梁彎曲變形和回彈變形的研究具有重要的理論意義和工程應用價值。為了方便敘述，彎曲直梁變形均為有限變形。

1 彎曲直梁的反耦聯系統和反耦聯方程

首先引入彎曲直梁的反耦聯系統和反耦聯方程的概念，考慮材料、形狀和尺寸相同，位移邊界條件相同，但體力及邊界力相反的兩直梁系統。其中之一為成形直梁，該直梁在加載時發生彈塑性變形。另一直梁成為回彈直梁，該直梁在加載時只發生彈性變形。成形直梁和回彈直梁構成彎曲直梁-反耦聯系統。成形直梁如圖1所示。

成形直梁的平衡方程、靜力邊界條件和位移邊界條件分別表示為

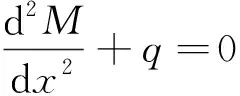
(1)

(2)

式中：M為成形直梁彎矩；Mx=0、Mx=l分別為成形直梁的梁左、右端彎矩；Wx=0、Wx=l分別為成形直梁的梁左、右端撓度。

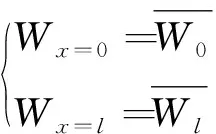
(3)

回彈直梁和相應的力學方程分別表示為

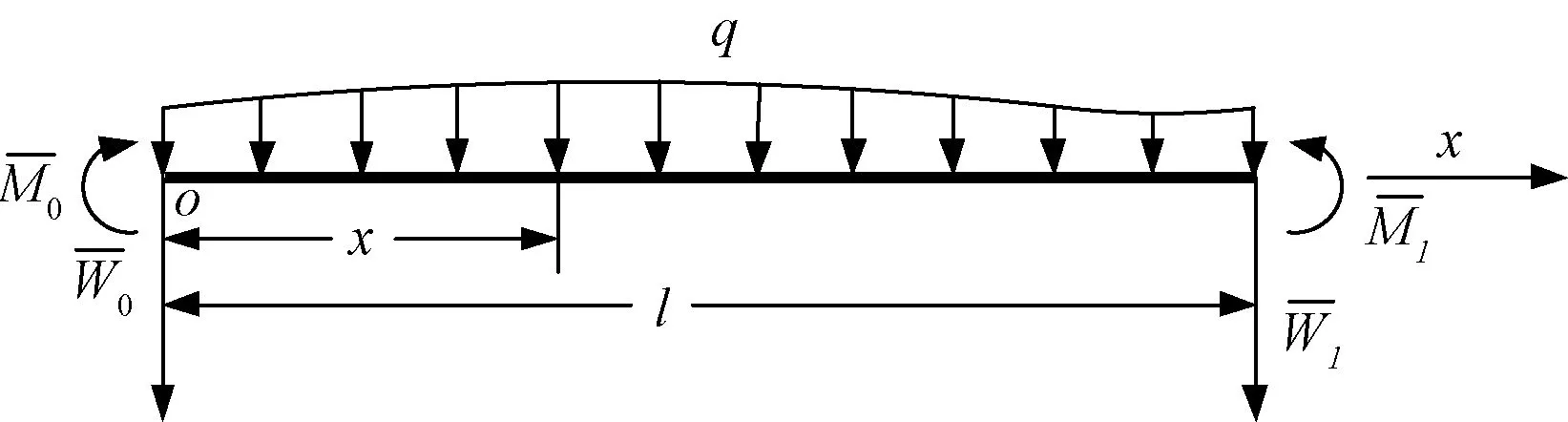
x為成形直梁從原點o到直梁上任意一點的距離；為梁左、右端彎矩；表示梁左、右端撓度；q為均布外荷載；l為跨度圖1 成形直梁Fig 1 Straight beam forming

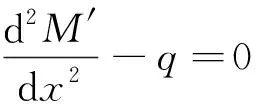
(4)

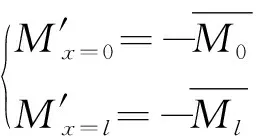
(5)

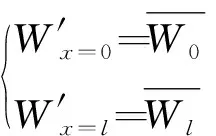
(6)

式中：M′為回彈直梁彎矩；M′x=0、M′x=l分別為回彈直梁的梁左、右端彎矩；W′x=0、W′x=l分別為回彈直梁的梁左、右端撓度。

式(1)～式(3)分別與式(4)～式(6)合并，則得方程為

(7)

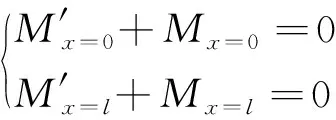
(8)

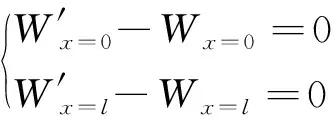
(9)

式中：式(7)為成形體與回彈體構成的反耦聯系統的反耦聯平衡方程；式(8)為反耦聯靜力邊界條件；式(9)為反耦聯位移邊界條件。

2 彎曲直梁的回彈變分原理

2.1 彎曲直梁的回彈最小勢能原理

采用加權余量法對式(7)、式(8)進行計算，則有：

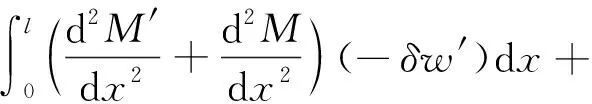
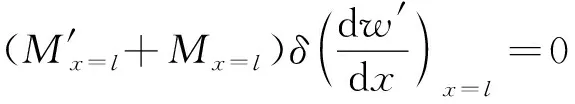
(10)

對式進行相應的變分運算。

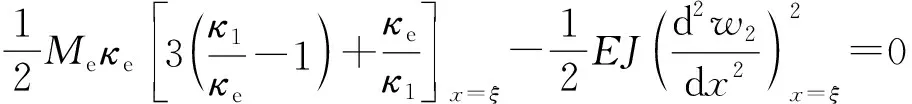
(11)

則得

(12)

式中：Π′sp為回彈直梁的彈性勢能；A(K′)為回彈勢能密度；式中：δ為變分極值；w′為回彈直梁的容許撓度；Me為梁水平方向彎矩κe為彈塑性區與彈性區交界處的轉角；κ1為彈塑性區的轉角；ξ為梁跨內彈塑性區長度；E為楊氏模量；J為慣性矩；A(K′)為回彈勢能密度；K′為回彈直梁彎曲曲率。

對式(13)進行變分運算。

(13)

則得

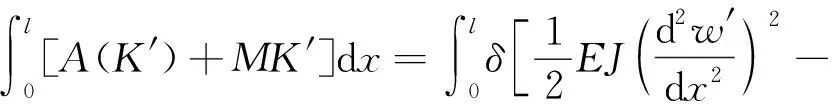
(14)

根據變分法基本預備定理，則得歐拉方程為

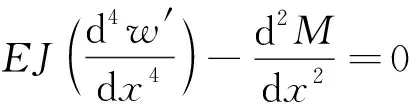
(15)

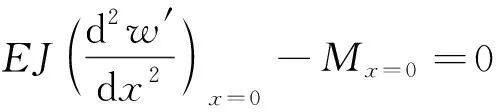
(16)

(17)

2.2 彎曲直梁的回彈最小余能原理

應用加權余量法，可得回彈總余能Π′sc為

(18)

因

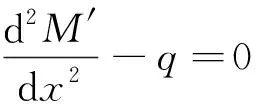
(19)

即

(20)

式中：B(M′)為回彈余能密度；K為成形直梁彎曲曲率；w為成形直梁的容許撓度。

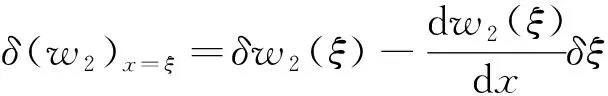
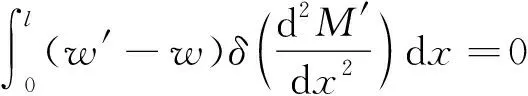
(21)

由于內力是容許的，故應滿足平衡方程和靜力邊界條件：

(22)

δM′x=0=δM′x=l=0

(23)

于是式(21)變為

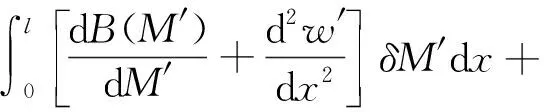
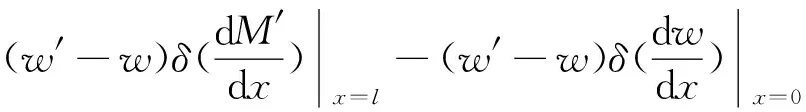
(24)

據變分法基本預備定理，則得歐拉方程為

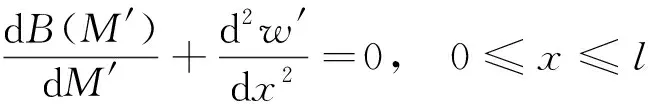
(25)

w′x=0-wx=0=0

(26)

w′x=l-wx=l=0

(27)

式中：wx=0、wx=l分別為成形直梁的梁左、右端容許撓度；w′x=0、w′x=l分別為回彈直梁的梁左、右端容許撓度。

3 彎曲直梁的廣義回彈變分原理

3.1 彎曲直梁的廣義回彈勢能原理

應用拉格朗日乘數法，可得廣義回彈勢能泛函數為

(w′-w)x=l(Q′+Q)x=l

(28)

式(28)中：Π′gsp為回彈直梁的廣義彈性勢能；Q、Q′分別為成形、回彈直梁剪力。

對式(28)取w′、K′和M′的變分駐值，則得:

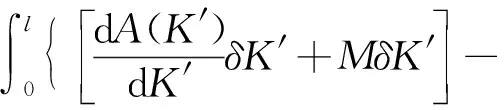
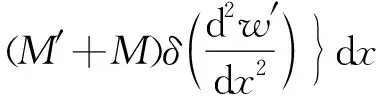
(w′-w)x=lδQ′x=l+(Q′+Q)x=0δw′x=0-

(Q′+Q)x=lδw′x=l=

(w′-w)x=0δQ′x=0-(w′-w)x=lδQ′x=l+

(Q′+Q)x=0δw′x=0-(Q′+Q)x=lδw′x=l=0

(29)

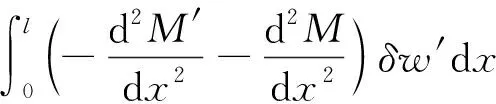
(30)

式(29)右端后兩項和式(30)右端后兩項相抵消，則式(28)變為

(w′-w)x=0δQ′x=0-(w′-w)x=lδQ′x=l-

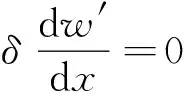
(31)

根據變分法基本預備定理，則歐拉方程為

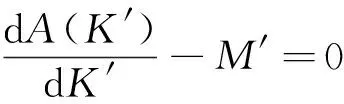
(32)

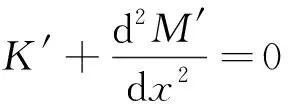
(33)

(34)

(w′-w)x=0=0

(35)

(w′-w)x=l=0

(36)

(M′+M)x=0=0

(37)

(M′+M)x=l=0

(38)

3.2 彎曲直梁的廣義回彈余能原理

應用拉格朗日乘數法，則得廣義余能泛函數為

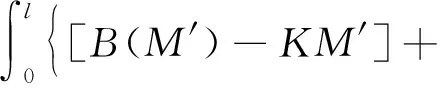
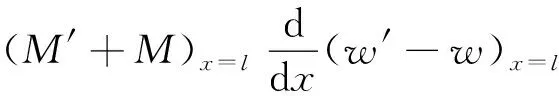
(39)

式(39)中：Π′gsc為回彈直梁的廣義彈性余能。

對式(39)M′、K′和w′取駐值變分，則得

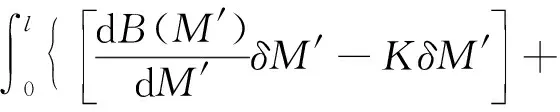
(40)

則式(40)變為

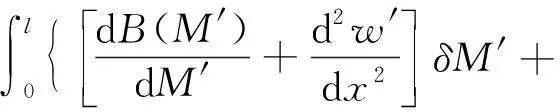
(41)

根據變分法基本預備定理，則得歐拉方程為

(42)

(43)

(M′+M)x=0=0

(44)

(M′+M)x=l=0

(45)

(w′-w)x=0=0

(46)

(w′-w)x=l=0

(47)

4 集中荷載作用下彈塑性懸臂梁回彈變分原理的應用

4.1 回彈變分最小勢能原理的應用

應用最小勢能原理計算想彈塑性材料懸臂梁的回彈變形。成形懸臂梁的任意截面彎矩為

M(x)=-P(l-x)

(48)

(49)

式中：P為成形直梁所受集中力。

于是有:

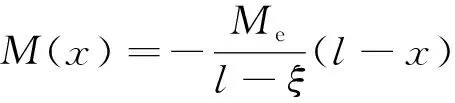
(50)

使回彈懸臂梁的容許位移為

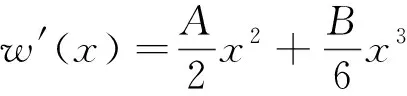
(51)

于是有：

(52)

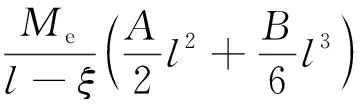
(53)

對式(53)中的Π′sp取A、B極值，得

(54)

將式(54)代入式(51)得回彈撓曲線方程為

(55)

4.2 回彈變分最小余能原理的應用

應用最小余能原理計算理想彈塑性材料懸臂梁的回彈變形。假設懸臂梁的任意截面彎矩為

M′(x)=-P′(Al-Bx)

(56)

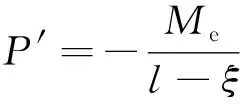
(57)

式中：M′(x)為回彈直梁在梁上一點出彎矩；P′為回彈直梁所受集中力。

于是有：

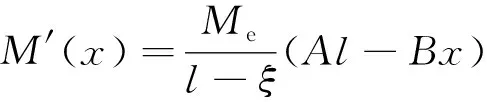
(58)

懸臂梁的容許位移為

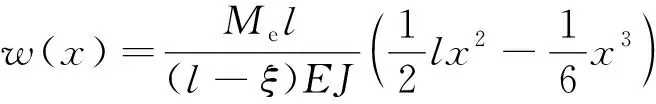
(59)

(60)

(61)

對Π′sc取A、B極值，得

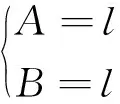
(62)

將式(62)代入式(58)，得到回彈撓曲軸方程為

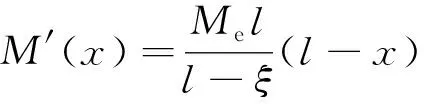
(63)

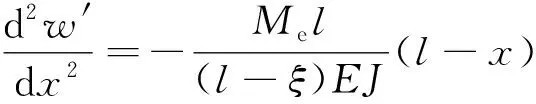
(64)

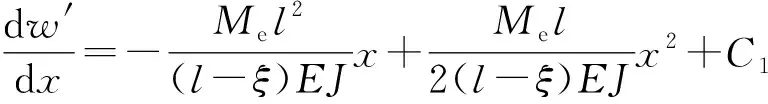
(65)

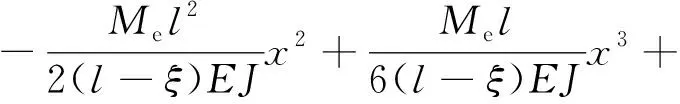
C1x+C2

(66)

式中：C1、C2為常量。

滿足的位移邊界條件：當x=0時

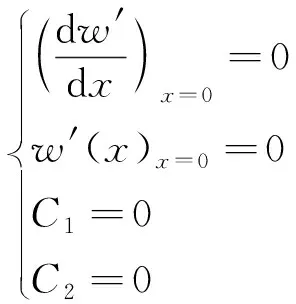
(67)

最后得回彈撓曲線方程為

(68)

4.3 有限元模擬以及數值計算

4.4 結果分析

從圖2可知，通過本文方法計算的懸臂梁回彈值與ANSYS模擬計算得出的懸臂梁回彈值基本吻合，其中最大相對誤差在允許范圍內。證明了應用回彈變分原理計算彈塑性懸臂梁的回彈撓曲線方程是正確的。

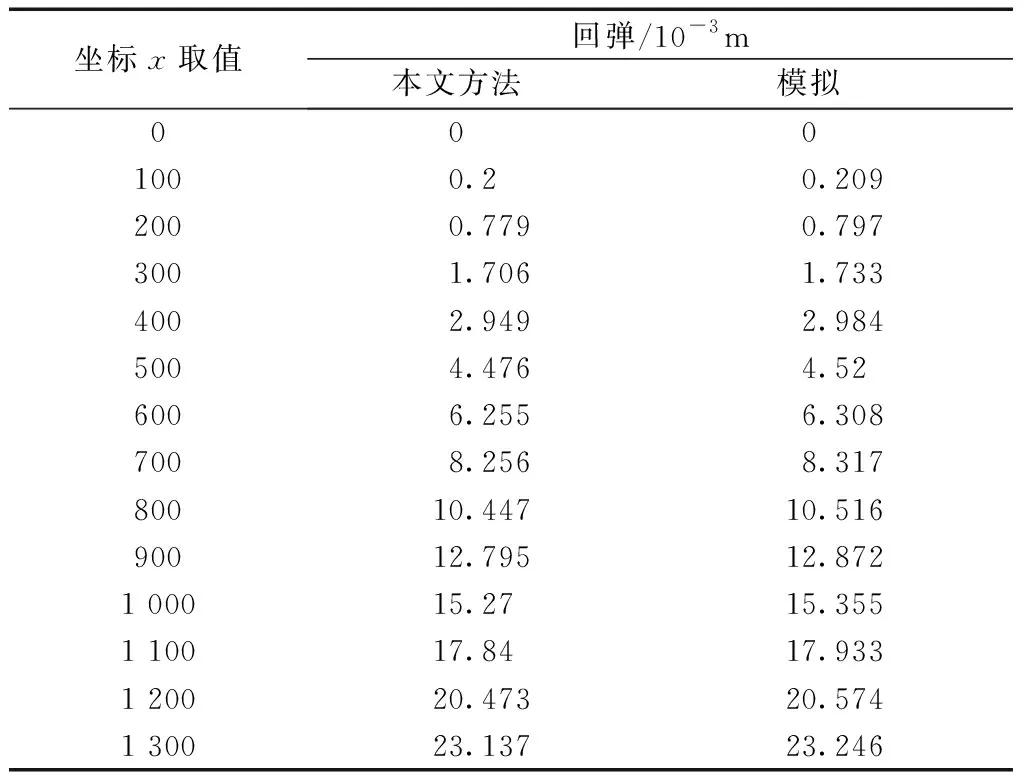
表1 當ηx=0(x)=0時本文方法與模擬的回彈數值Table 1 The proposed method and numerical simulation of spring back when ηx=0(x)=0

圖2 固定端截面彈性區高度不同時梁的回彈變形Fig.2 Springback deformation of beams with different height of elastic zone of fixed end section

5 集中荷載作用下彈塑性簡支梁回彈變分原理應用

5.1 回彈變分最小勢能原理的應用

應用最小勢能原理計算想彈塑性材料簡支梁的回彈變形。簡支梁的任意截面彎矩為

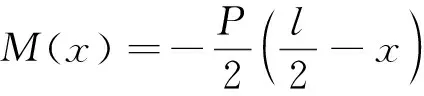
(69)

(70)

于是有：

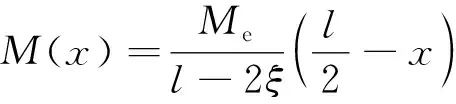
(71)

假使簡支梁的容許位移為

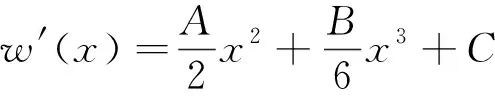
(72)

于是有：

(73)

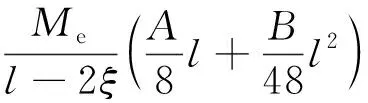
(74)

對Π′sp取A、B極值，得

(75)

將式(75)代入(72)得到回彈撓曲線方程為

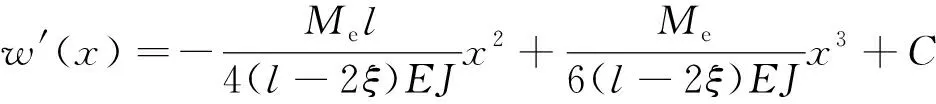
(76)

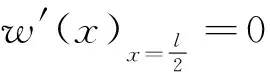
(77)

(78)

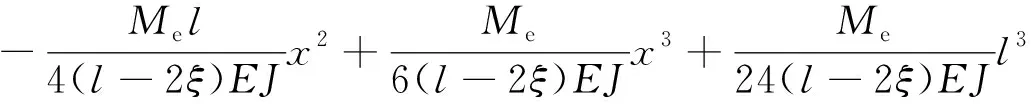
(79)

5.2 回彈變分最小余能原理的應用

應用最小余能原理計算理想彈塑性材料簡支梁的回彈變形。假設簡支梁的任意截面彎矩為

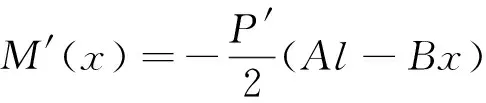
(80)

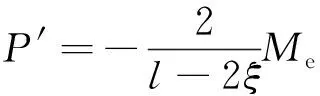
(81)

于是有：

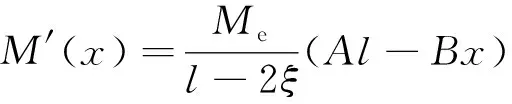
(82)

梁的容許位移為

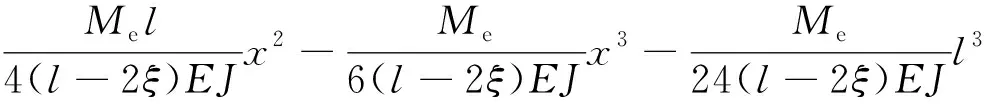
(83)

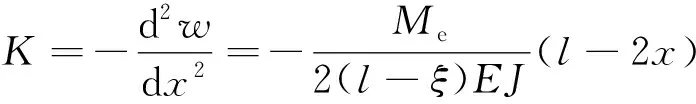
(84)

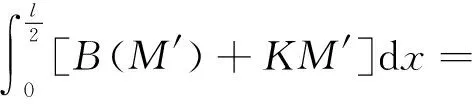
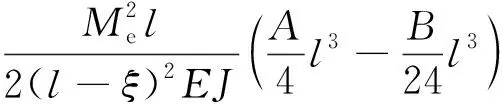
(85)

對Π′sc取A、B極值，得

(86)

最后得回彈撓曲軸方程為

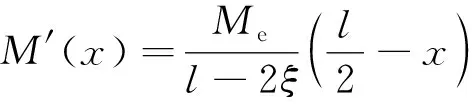
(87)

(88)

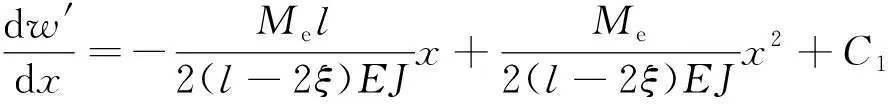
(89)

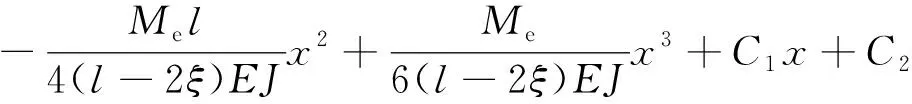
(90)

為滿足位移邊界條件，當x=0時

(91)

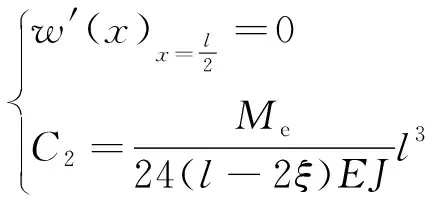
(92)

最后得回彈撓曲線方程為

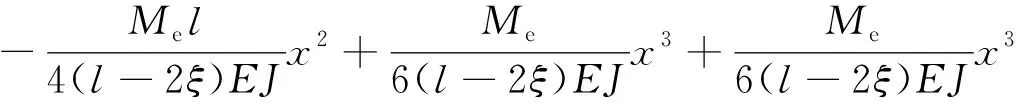
(93)

5.3 有限元模擬以及數值計算

表2 當ηx=0(x)=0時本文方法與模擬的回彈數值

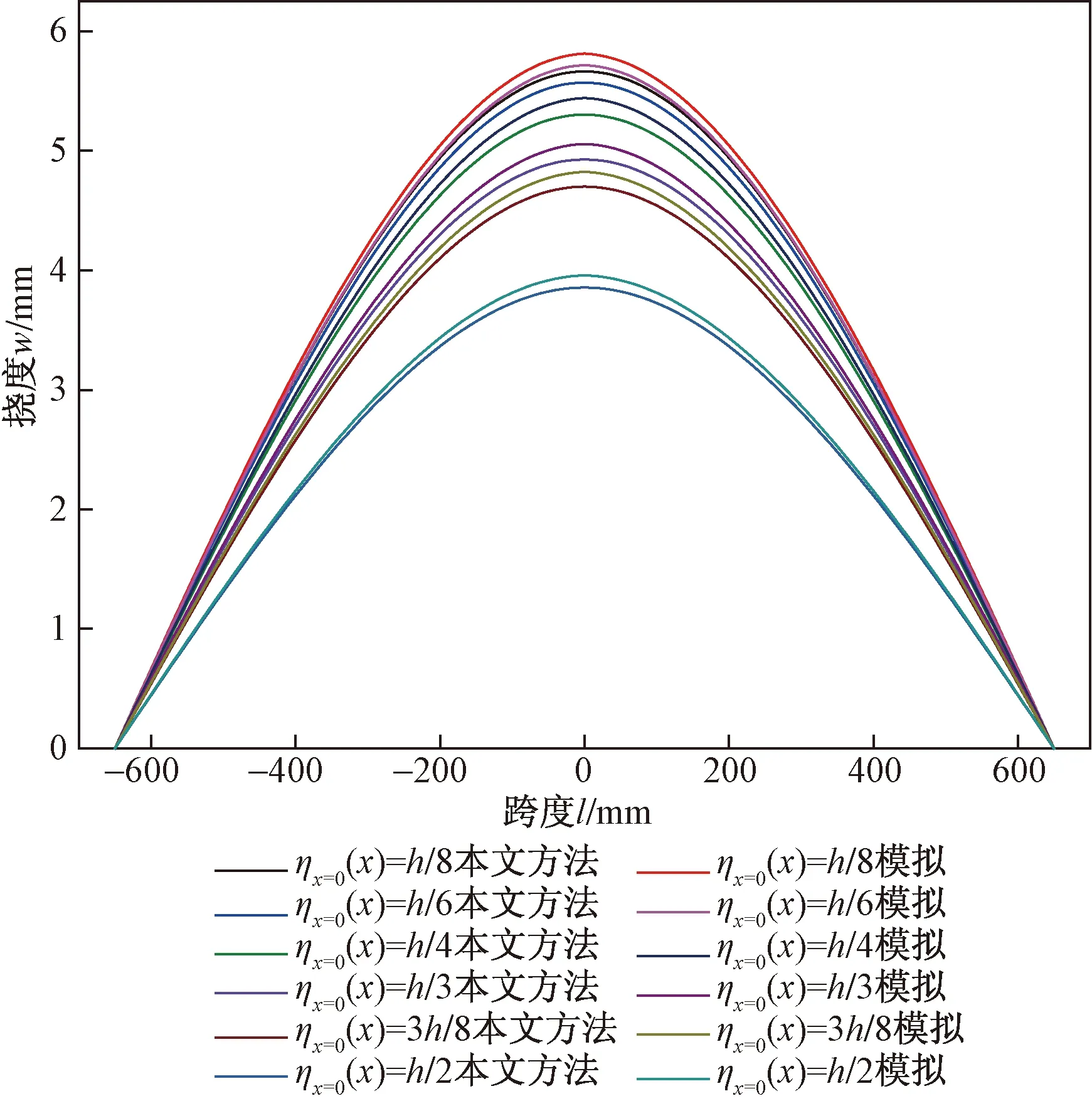
圖3 跨中截面彈性區高度不同時梁的回彈變形Fig.3 Springback deformation of beams with different height in elastic zone of mid-span section

5.4 結果分析

從圖3可知，通過本文方法計算的懸臂梁回彈值與ANSYS模擬計算得出的懸臂梁回彈值基本吻合，其中最大相對誤差在允許范圍內。從而證明，應用本文研究的回彈變分原理計算彈塑性懸臂梁的回彈撓曲線方程是正確的。

6 結論

主要闡述了彈塑性彎曲直梁回彈變分原理在理想彈塑性懸臂梁和理想彈塑性簡支梁中的應用。建立了彈塑性彎曲直梁的耦聯系統和反耦聯系統，由反耦聯系統推導出反耦聯方程，并應用加權余量法得到了回彈變分原理，并通過最小勢能原理和最小余能原理推導出彈塑性彎曲直梁變形后的回彈撓曲線方程。根據梁上的荷載條件，聯立不同的邊界條件進行求解，最終得到回彈撓度值。然后應用ANSYS進行實體建模分析，得到具體計算結果。最后將兩種計算結果分別進行對比，證明了所推導彈塑性彎曲直梁回彈變分原理的正確性，因此本文方法在工程應用計算中具有一定的參考價值和科學理論意義。