一種基于正則化方法的非負矩陣分解算法研究與應用

李小珍

(安徽國防科技職業學院，安徽 六安 237001)

0 引言

非負矩陣分解(NMF)是由學者Lee和Seung首次提出的矩陣分析方法，隨著信息化技術的快速發展，矩陣分解在大數據處理和模式識別中發揮著越來越重要的作用[1]。傳統的矩陣分解工具，結果中普遍含有負數，這為實際應用帶來了一定的難度。與此不同的是，非負矩陣分解的所有結果均為非負值，對象的物理表達更加自然，具有更加廣闊的應用前景。但是傳統非負矩陣分解方法無法同時考慮數據樣本特征信息和數據固有幾何結構，在一定程度上影響了數據的聚類結果。本文將圖正則化方法和半監督學習思想深度結合起來，提出新的非負矩陣分解算法。該方法充分考慮樣本的類別信息和數據空間的幾何流行結構信息的有效性，并以圖像聚類為例，選擇ORL數據集進行算法驗證[2]。

1 圖像分類與模式識別

圖像數據的維度較高，直接影響了圖像分類的準確性和運算效率，所以圖像分類的第一步就是圖像降維。降維能夠去掉冗余的維數，將有用的維數保留下來，實現高維數據低秩逼近。圖1所示為圖像分類的基本框架，首先通過圖像降維處理獲得圖的特征值、特征向量，然后將其輸入分類器或者支持向量機，以此實現圖像分類。

圖1 圖像分類的框架

2 非負矩陣分解

2.1 非負矩陣分解的基本概念

對非負矩陣X∈Rm×n來說，矩陣分解的目標就是為了得到兩個非負矩陣W∈Rm×r和H∈Rr×n，使得X≈WH，其中r=min(m,n)。X≈WH的求解可以近似看做是求最優解的問題。常用的非負矩陣分解的目標函數有基于歐式距離和基于K-L散度兩類。

基于歐式距離的目標函數可以表示為：

(1)

基于K-L散度的目標函數可以表示為：

-Xij+(WH)ij)2

(2)

在統計獨立性方面，K-L散度具有突出優勢。K-L散度是X和WHT差異的非對稱性度量。當X=WHT，K-L散度函數最小值為0。如果單獨分析矩陣W和H，那么上文提到的目標函數為凸函數；如果同時考慮矩陣W和H，那么目標函數不是凸函數。非負矩陣分解之后的矩陣W和H具有稀疏性，可以有效的降低數據冗余。但是，這種方法帶來的稀疏性不夠明顯，很多情況下無法滿足應用要求，所以需要在目標函數中增加稀疏限制項。非負矩陣分解算法及其常見的改進算法中，矩陣W和H的初始值都是隨機選擇的，這些隨機值均為非負值。如果實際問題相關信息不明確，那么W和H的初始值無法確定，只能隨機選擇。非負矩陣分解算法類似于約束優化問題，執行問題的步驟復雜繁多，選擇最優分解也帶來了很大的時間消耗，無法滿足實踐應用需要[3]。

2.2 迭代規則及算法收斂性

利用乘性迭代算法更新W，利用交替迭代算法更新H，不僅能夠提升收斂速度，也能夠降低計算難度。

Lee和Seung[4]提出一種乘法更新算法，將(1)更新為：

(3)

式(2)的更新規則可以表示為：

(4)

其中1≤i≤m,1≤j≤n,1≤k≤r，轉置矩陣表示為T，基矩陣表示為W，其中的列稱為基向量，系數矩陣表示為H。矩陣W和H的初始值隨機，在運算過程中不斷更新矩陣W和H的值，直到矩陣的變化足夠小，獲得矩陣分解結果。為了確保更新過程中不因為分母為零而導致異常，在分母上要添加一個足夠小的正數。

歐式距離函數(1)單調遞減，如果W和H是函數的穩定點，那么函數值不再繼續變化。

K-L散度函數(2)單調遞減，如果W和H是函數的穩定點，那么函數值不再繼續變化。

在討論非負矩陣分解算法的收斂性時，引入了輔助函數[5]來分析，并導出迭代規則。

定義G(k,k′)為F(k)的輔助函數，并且滿足式：

G(k,kt)≥F(k),G(k,k)=F(k)

(5)

2.3 圖正則非負矩陣分解算法

采用圖正則化方法的非負矩陣分解算法，就是在進行矩陣分解時，明確低維度空間樣本數據的基本幾何結構。假設存在兩個數據點，分別表示為xi和xj，它們在原數據空間是鄰近的關系，那么在新的基矩陣下其對應的vi和vj也是鄰近關系。

假設G是由原始數據點組成的圖，權重矩陣用Sij來表示，xi的p個鄰近數據點由Np(xi)表示，那么：

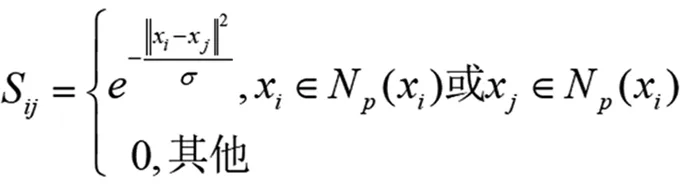
(6)

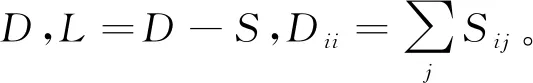
式(7)為圖正則化非負矩陣分解算法的最小化目標函數：

(7)

迭代更新規則表示為：

(8)

3 基于圖正則化和稀疏約束的半監督非負矩陣分解

在特征提取方面，非負矩陣分解算法只能在數據原始空間展開，在變形空間無法實現。本文提出在非負矩陣分解算法基礎上，對基矩陣進行稀疏約束，引入拉普拉斯正則化約束，最終有效減少運算環節和節約存儲空間，提升非負矩陣分解的效率。

本文提出的新的最小化目標函數可以表示為：

(9)

上式中，標簽約束矩陣可以表示為A，拉普拉斯矩陣表示為L，正則化參數表示為λ，稀疏系數表示為β，β∈(0,1)。‖g‖F表示的是F范數。按照迭代法和最速下降法的原則，式(9)的迭代規則可以表示為：

=Tr(XXT)-2Tr(SAZWT)+Tr(WZTATAZWT)

(10)

φ和φ表示的是約束Wik≥0,Zjk≥0對應的拉格朗日乘子，那么可以將拉格朗日函數表示為：

L1=OF+Tr(φWT)+Tr(φZT)

(11)

求解W和Z的偏導數，令它們的值為零，那么：

(12)

利用KKT條件，可以將迭代規則確定為：

(13)

根據上述分析，目標函數和Z中任意元素Zij相關的部分可以表示為Fij，那么：

(14)

此處假設F′表示的是Z的一階微分，那么Fij的輔助函數可以表示為：

(15)

證明G(z,z)=Fij，按照輔助函數的定義，則需要證明G(z,zt)≥Fij(z)。Fij(z)的泰勒展開可以表示為：

(16)

相較于輔助函數，可以將G(z,zt)≥Fij(z)等價表示為：

≥(AAT)ii(WTW)jj+λ(ATLA)ii

(17)

已知

≥zt(ATA)(WTW)

(18)

且

≥λ(AT(D-U))zt=λ(ATLA)zt

(19)

得證。

4 實驗驗證

在Windows10環境下，利用Matlab R2012b進行算法的驗證。此次驗證基于英國劍橋Olivetti實驗室提出的人臉圖像數據庫ORL展開。所有圖像的尺寸都是92×112。ORL數據集共有400張圖片，維度為1024，共40個類別。

首先從ORL數據集的各個樣本類中選取包含有標記信息的樣本，從其中隨機的選擇K類樣本開展聚類分析，本文選定的實驗次數為20次。

圖2 ORL數據庫的圖像舉例

算法的聚類性能采用聚類準確率(AC)的指標來分析，即數據集中正確分類的樣本的占比。如果樣本的數據量為n，ri表示給定的正確樣本類別信息，li表示聚類后的樣本信息。則

(20)

上式中，δ(x,y)表示二值函數。如果x=y，那么二值函數值為1；如果x≠y，那么值為0。map(li)表示映射函數，是li和數據集中其他類別的樣本之間的映射關系。

互信息表示聚類樣本之間存在的相關性，即MI。假設存在兩個聚類樣本集，分別表示為C和C′，則：

MI(C,C′)

(21)

將其歸一化之后，可以表示為：

(22)

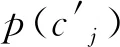
此處正則項參數λ取值為100，稀疏系數β的取值為0.3。

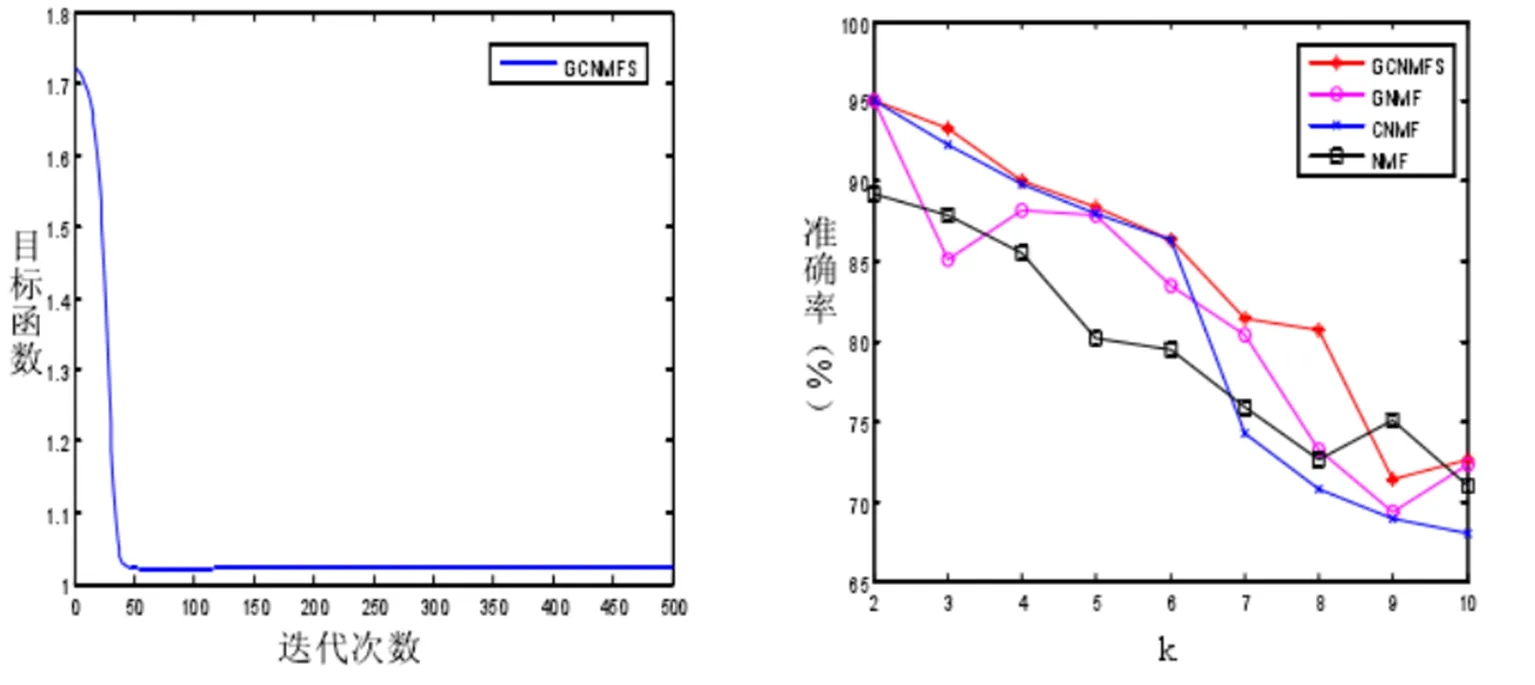
圖3 ORL數據集的收斂曲線及聚類準確率

圖3所示為利用ORL數據集實驗后的收斂曲線，實驗結果表明利用該方法迭代50次左右就能夠滿足收斂要求。采用幾種不同的非負矩陣分解算法，對每個隨機的k值運行20次后，最終的聚類結果表明該算法在圖像聚類方面效率良好。

5 結語

總體來看，利用本文提出的新的非負矩陣分解算法，降維之后的圖像聚類效果遠好于一般的非負矩陣分解算法，并且穩定性能保持在良好的范圍內，該算法在圖像分類中有良好的應用效果。