高維廣義具阻尼項(xiàng)的Bq方程解的整體存在性和衰減行為

李梅玲，王云青

( 渤海理工職業(yè)學(xué)院 基礎(chǔ)部，河北 滄州 061199)

0 引言

本文主要考察下面一類(lèi)Bq方程的柯西問(wèn)題

utt-Δu-aΔutt+Δ2u+Δ2utt-bΔut

=Δf(u),x∈Rn,t>0

(1)

u(x,0)=u0(x),ut(x,0)=u1(x),x∈Rn

(2)

其中u(x,t)表示未知函數(shù)，u0和u1是給定的初始函數(shù)值，Δ是n維拉普拉斯算子，a,b>0為常數(shù)。很多數(shù)學(xué)家和物理學(xué)家研究了帶有色散項(xiàng)或者耗散項(xiàng)的Bq方程的衰減[1-2]，但很少有人研究既帶有色散項(xiàng)又帶有耗散項(xiàng)的衰減結(jié)果。Wang等人給出了當(dāng)a=b=1時(shí)此問(wèn)題解的整體存在性和衰減行為[3]。Piskin等人研究了當(dāng)a=2時(shí)上述問(wèn)題解的整體存在性和衰減估計(jì)[4]。本文主要研究帶有色散項(xiàng)和耗散項(xiàng)的Bq方程的柯西問(wèn)題及衰減行為。

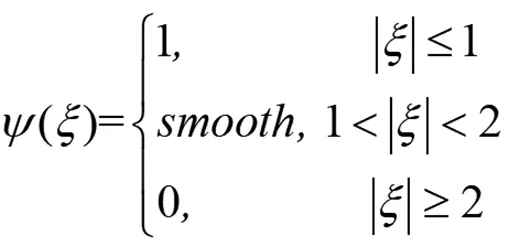
記號(hào)AB表示A≤CB，其中C>0為每一個(gè)常數(shù)的同一個(gè)標(biāo)志。

1 對(duì)應(yīng)線(xiàn)性方程解的衰減估計(jì)

研究下面線(xiàn)性問(wèn)題解的衰減性

utt-Δu-aΔutt+Δ2u+Δ2utt-bΔut

=Δg(x,t)，x∈Rn,t>0

(3)

u(x,0)=u0(x),ut(x,0)=u1(x),x∈Rn

上述問(wèn)題的形式解為

u(x,t)=H(t)u0+G(t)u1

(4)

格林算子

G(t)=F-1L(ξ,t)F，H(t)=F-1L1(ξ,t)F

其特征是

其中ω(ξ)=

(5)

為估計(jì)線(xiàn)性問(wèn)題的衰減性，引入m階Bessel函數(shù)Jm(r)的一些性質(zhì)[5]，徑向函數(shù)f(x)=f(|x|)的傅里葉變換仍然是一個(gè)徑向函數(shù)，且

引理1[3]假設(shè)φj(ξ)=φ(2-jξ)，supφj?{ξ:2j-1≤|ξ|≤2j+1}，ω(ξ)=ω(|ξ|),由(5)式定義，則當(dāng)j≤0時(shí)，下面不等式成立

(6)

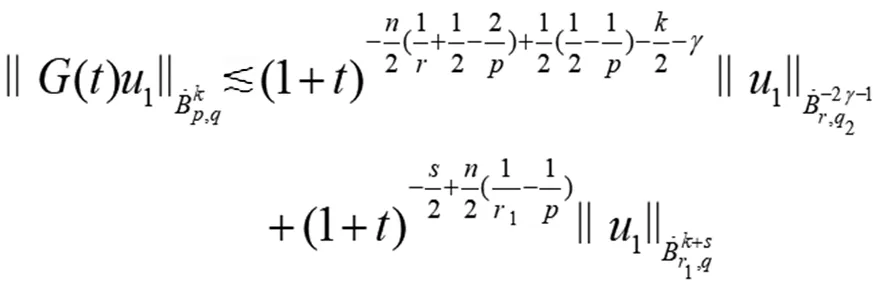
(7)

(8)

(9)

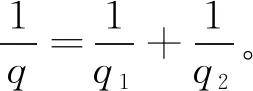
證明由齊次Besov空間的范數(shù)定義知，對(duì)?u1∈S，有

對(duì)于A(yíng)1，由Bernstein不等式和Young不等式，注意到ξ∈supφj?{ξ:2j-1≤|ξ|≤2j+1}，有

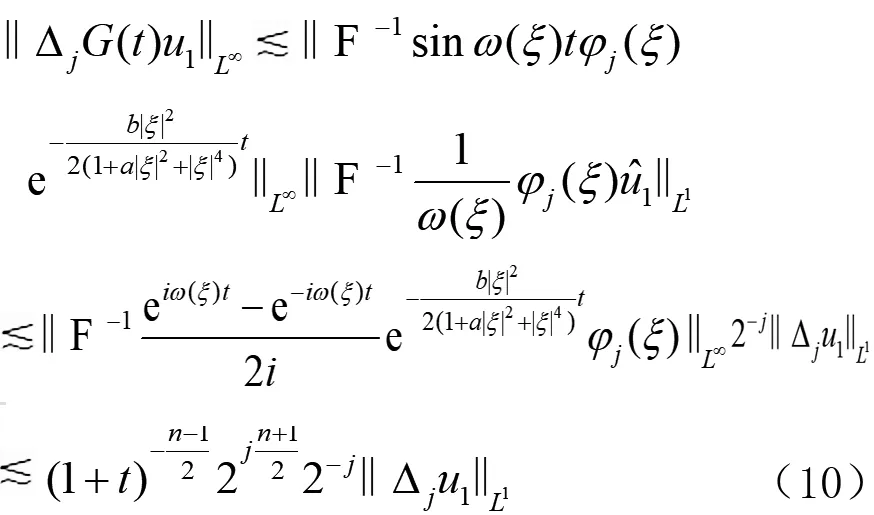
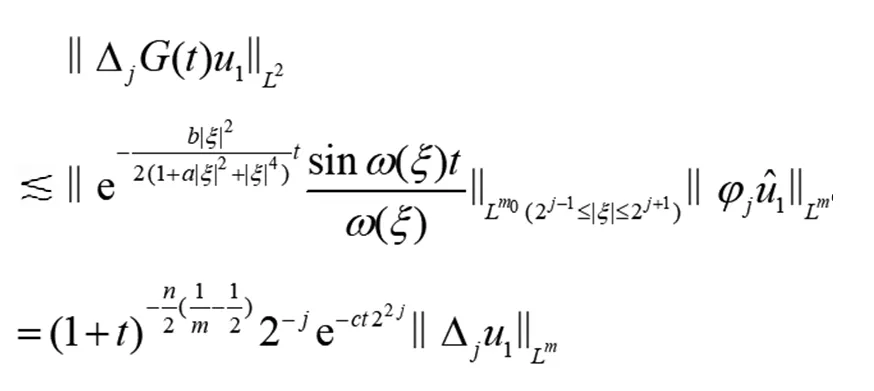
(11)

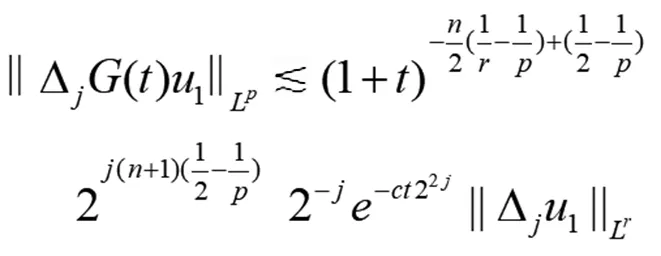
(12)

(12)式兩邊乘以2jk后，再取Lp范數(shù)(j≤0)，得

(13)

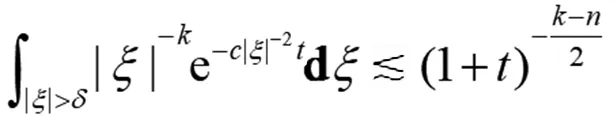
(14)

類(lèi)似方法可證(8)和(9)式。

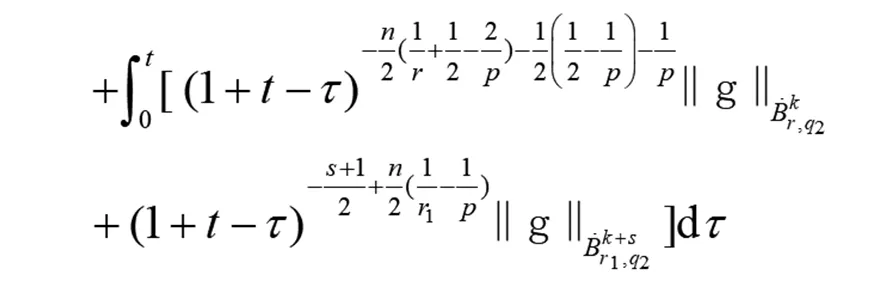
(15)

(16)

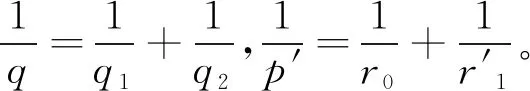
證明由杜哈密頓原理，易得問(wèn)題(1)、(2)解的存在唯一性。(15)式由定理1和(4)式可得。因?yàn)?/p>

ut(x,t)=Ht(t)u0+Gt(t)u1

類(lèi)似于定理1可證(16)式。

2 主要結(jié)果

引理2[3]對(duì)任意s≥0，f∈C{s}(R)，滿(mǎn)足條件

|f(j)(u)||u|α-j,j=0,1,…,{s},{s}≤α

(17)

則對(duì)?u∈R，有

(18)

引理3[6]假設(shè)a,b為兩個(gè)正數(shù)，則

(19)

(20)

(21)

其中常數(shù)C只依賴(lài)于f。

證明首先，我們定義空間(X,d)上的非線(xiàn)性映射N(xiāo)

N(u)=H(t)u0+G(t)u1

(22)

且對(duì)?u，v∈X。d(u,v)=‖u-v‖L∞([0,+∞);L2)。易證，(X，d)是一個(gè)完備度量空間。

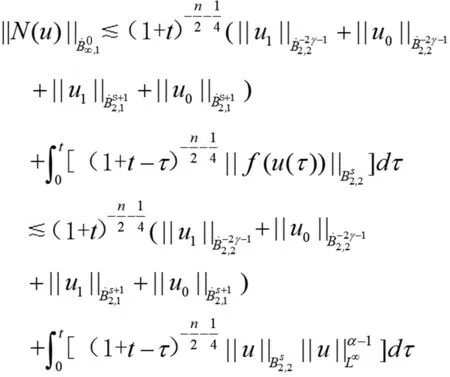
(23)

(24)

(25)

由(24)式和(25)式，有

(26)

對(duì)?u，v∈X,由(22)式，知

N(u)-N(v)

在(15)式中取k=0,s=0,p=2,q=q2=2，r1=r=2,得

即對(duì)充分小的ρ，N是X到自身的嚴(yán)格壓縮映射。利用壓縮映射原理，知N(u)在X上存在唯一不動(dòng)點(diǎn)u(x,t)，u(x,t)是問(wèn)題(1)、(2)的解，且

u(x,t)=H(t)u0+G(t)u1

由標(biāo)準(zhǔn)理論可得到解u(x,t)的時(shí)間連續(xù)性。