HPM視角下“解析幾何序言課”實踐與研究

龐海燕

[摘? 要] 在新的教學理念下，我們由研究知識傳授轉向研究全程育人、綜合育人、全面育人，從學科教學走向學科教育，以發展學生的核心素養，即從“知識、能力本位”走向“素養本位”. 文章以浙江省義烏市王芳名師工作室經過“三試三議 ”模式開發的高中數學HPM序言課為例，進行解析幾何序言課的探究和實踐.

[關鍵詞] HPM;解析幾何;序言課;坐標法

引言

教育部印發了《關于全面深化課程改革落實立德樹人根本任務的意見》，要求我們由研究知識傳授轉向研究全程育人、綜合育人、全面育人，也就是從學科教學走向學科教育，確立了以發展學生的核心素養為目標，即從“知識、能力本位”走向“素養本位”. 核心素養是學生通過學科學習而形成的正確的價值觀念、必備品格和關鍵能力，通俗地講，就是那些很多年后宏觀留下的進入學生靈魂深處的東西，因此與之相適應的應該是注重整體一致與邏輯連貫的教學. 正是因為序言教學能滿足這些需求，目前很多學者不約而同地提出序言教學. 序言課能為整章的教學起到路線規劃、導航定位的作用，相當于汽車GPS（全球定位系統）的功能. 安裝了“GPS”的起始教學能讓后續課時教學近似于“傻瓜式”操作，避免我們走彎路，而且能加強整體認識，協調彼此之間的聯系. 如何設計、安裝理想的“GPS”呢？這其實就是序言課的設計、教學問題. 為了教學的整體性，我們需要從宏觀層面俯瞰課程的知識體系. 為了高觀點，我們需要從思想、觀念或者應用的層面提出問題、發現問題，不是簡單、日常意義上的數學題. 為了情境創設的適切性，我們需要運用歷史發生學原理，以史為鑒. HPM視角下的序言課課例研究可以有效促進教師在知識、信念和能力這三個維度的發展. 數學史融入數學序言課教學，可以呈現知識之諧，展示方法之美，營造探究之樂，揭示文化之魅，提供能力之柱，彰顯德育之效.

歷史材料及應用

本節課從回顧初中平面幾何知識和研究方法出發，讓學生經歷用演繹法解決平面幾何問題時遇到的困境，使學生感受到從單純觀察形的角度和科學技術發展的角度研究圖形的乏力，由此創設了“圓還是橢圓”的問題情境，以便激發學生進行方法的創新，產生突破的沖動. 這具有高度的歷史相似性：16世紀，對運動與變化研究已變成了自然科學的中心問題，原有幾何學出現解決問題乏力的狀態，迫切需要一種新的數學工具，從而導致了變量數學的產生.

在坐標法建構環節，先出示學生熟悉的兩個平面幾何問題，落腳點在用點的坐標刻畫距離、位置關系，再從靜到動，給出兩個古希臘軌跡問題，引出用坐標法研究點的位置、點的運動——曲線、圖形. 在此過程中運用史料：笛卡爾以研究古希臘軌跡問題為目的，以韋達的符號代數為工具，通過建立坐標系（一條軸），將二元代數方程與幾何曲線對應起來，從而成了解析幾何的發明者. 笛卡爾的解析幾何是作為《方法論》一書的附錄《幾何》出現的，后半部分通過展現解“帕普斯問題”的具體過程介紹了解析幾何方法，所謂笛卡爾解析幾何主要就體現在這一部分中.

在核心問題研究環節，強調用代數方法研究幾何圖形，設計橢圓規實驗;在知識展望環節，通過幾何畫板演示二元二次方程對應的曲線. 在此過程中運用史料：解析幾何的另一創始人17世紀法國數學家費馬從方程的角度出發研究曲線，笛卡爾的側重點是研究曲線的方程，兩者分別是解析幾何的兩個基本方面.

教學設計與實施

本節課突出“五核”，通過“圓還是橢圓”的情境創設，設置了數學問題串，建構起核心方法（坐標法），初步運用其解決核心問題（由曲線上點的特征建立方程、用代數方法研究幾何圖形、由方程研究曲線幾何性質及曲線位置關系），通過問題“這方法可靠嗎”直指核心概念（曲線的方程、方程的曲線），幫助學生理解和體會笛卡爾“一切問題都可歸結為數學問題，一切數學問題都可歸結為代數問題，一切代數問題都可歸結為解方程問題”的思想. 整節課滲透數形結合的核心思想，落實數學抽象、邏輯推理、數學運算的核心素養. 本節課以能在具體情境和解決問題的過程中，深化對坐標法的認識，感受解析幾何的孕育與發展為目標，重點在坐標法解決幾何問題思想的滲透，突破曲線與方程對應的難點.

（一）舊知回顧

教師：同學們好，今天我們要來說說幾何，初中的時候，我們學習了平面幾何，還記得我們學了哪些知識嗎？

學生：圖形認識初步、平行線、相交線關系、三角形、四邊形、圓.

教師：我們是用什么方法來研究這些幾何問題的呢？

學生：演繹法.

教師：初中平面幾何屬于歐氏幾何，歐幾里得的《幾何原本》首次建立起幾何學的完整演繹體系. 古希臘數學家阿波羅尼斯的《圓錐曲線論》幾乎包含圓錐曲線的全部性質. 那同學們在處理平面幾何問題時，用演繹法解決起來會碰到哪些困難呢？

學生討論，認為平面幾何沒有普適性的方法.

（二）情境創設

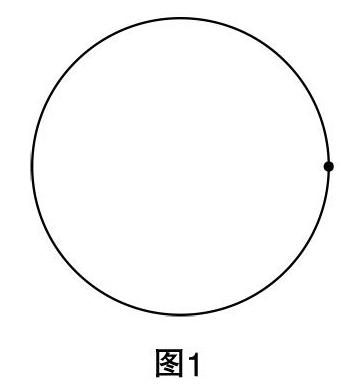
教師：我們今天的問題就從一張圖片說起，請觀察這張圖片，淺色曲線是什么？

學生：圓.

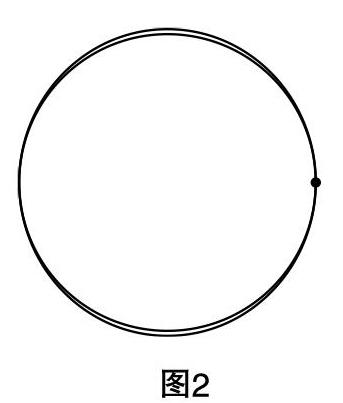
教師：再觀察一下（以深色曲線為參照）.

學生：橢圓？圓？

教師：哈哈，到底是圓還是橢圓呢？這樣的問題也曾困擾了一大批天文學家，下面請大家看一個視頻. （演示開普勒視頻）. 看完請同學們提取開普勒解決地球軌道是圓還是橢圓的關鍵詞.

學生討論得出“代數、幾何結合”“根據數據計算”等等.

教師：16世紀以后，科學的發展向幾何學提出了用運動的觀點來認識和處理圓錐曲線及其他幾何曲線的課題，之前歐氏幾何和阿波羅尼斯的圓錐曲線論中的方法已不能滿足人們的研究需要. 同學們說得都很好，那究竟會是一種什么樣的方法可以解決這些問題呢？代數、幾何如何結合？如何計算呢？

（三）方法建構

問題1：（1）正方形ABCD的邊長為6，E在邊AB上，BE=4，EF∥BC，分別交BD，CD于G，F，若M，N分別是DG，EC的中點，試求MN的長度.

（2）矩形ABCD中，E，F是CD上的三等分點，G，H是BC邊上的三等分點，AE與DG相交于K，AF與DH相交于N，求證：KN∥CD.

學生討論求解.

教師總結：幾何問題代數化，建立平面坐標系. 點的坐標來聯系，算出長度沒問題，平行關系可判定.

設計意圖：建立坐標觀念確定點的位置.

教師：靜止是相對的，運動是絕對的. 數學因運動而不再枯燥，數學因運動而充滿活力. 如何描述一個點在平面中的運動呢？

學生：用坐標刻畫點，點在平面內運動，其橫、縱坐標應該會滿足一定的關系.

問題2：（二線軌跡）阿波羅尼斯是公元前3世紀的古希臘著名數學家，他曾提出過這樣一個問題：到兩條互相垂直的直線距離相等的點的軌跡是什么？

學生：是這兩條直線所夾角的角平分線.

教師：那現在這兩條直線有幾條角平分線呢？

學生：兩條.

教師：很好. 根據初中所學平面幾何的知識，角平分線上的點到角兩邊的距離相等，因此在這個例子中我們可以很快得出“二線問題”的軌跡. 形狀、位置我們都可以定下來. 我們接下來再看一個升級版的問題.

問題3：（三線軌跡）古希臘數學家并不滿足于此，帕普斯又提出了“三線軌跡”問題. 如圖5，平面內三條直線滿足l■⊥l■，l■⊥l■，l■∥l■，l■，l■距離為a，平面上一動點P到l■，l■，l■的距離PA，PB，PC滿足PA·PB=PC2，動點P的運動軌跡是什么？

是否與剛剛的二線軌跡問題一樣，可以一眼就看出點的軌跡呢？

學生討論解決方案：以l■，l■交點為原點建系，設點P（x，y），得出（x，y）滿足方程x-■■+y2=■■.

教師：這個方程代表著什么意義呢？對于二元方程x-■■+y2=■■，這種通常有無窮多組解的所謂“不定方程”對代數學家來說是索然無趣的，但如果注意到當x連續地改變時，方程相應確定y，于是兩個變量的組合（x，y）可以看作是平面上運動著的點的坐標，于是這樣的點組成一條平面曲線.

學生：得出方程表示P（x，y）到■，0距離為定值■，是一個以■，0為圓心，■為半徑的圓.

設計意圖：引導學生建立將帶兩個未知數的方程和平面上的曲線相對比的觀念.

教師：很好，大家以前是否有看見一個方程，就知道它表示什么曲線的這種經歷嗎？

學生：有，形如y=kx+b的表示直線，形如xy=k的表示雙曲線，形如y=ax2+bx+c（a≠0）的表示拋物線.

教師：很好，方程中的x，y有什么幾何意義和代數意義嗎？

學生：從代數角度，有序數對（x，y）表示方程的解;從幾何角度，有序數對（x，y）表示曲線上某點的坐標.

教師：有序數對（x，y）從哪里來的呢？

學生：建系.

教師：對！我們坐標系這個工具溝通起方程的解和曲線的點，可以把幾何問題轉換為代數操作，幾何運動轉化為代數方程，從研究代數、方程的角度來研究幾何問題. 讓我們給這個操作起個名字吧！

學生：建系法！坐標法！

教師總結：坐標法就是通過建立坐標系，將幾何問題轉化為代數問題，再通過一步步地計算來解決問題的方法.

引導學生總結坐標法解決幾何問題的步驟.

（四）核心問題

教師：坐標法可以干什么呢？我們如何解決前面“圓還是橢圓”的問題？

1. 圓心在坐標原點的單位圓上任意一點P（x，y），滿足的條件是________.

（1）y=■可以表示1中的圓嗎？

（2）點■，■，■，-■在1中的圓上嗎？

教師總結：從曲線幾何特征寫曲線的方程，再從方程形式判斷曲線的形狀，我們發現曲線上的點與方程的解一一對應，故而坐標法可以由曲線上點的特征建立方程.

小組動手實驗探究：荷蘭數學家蘇騰的橢圓作圖工具中的兩種.

實驗結論：平面上一個動點到兩定點距離之和（和值大于兩定點之間的距離）等于定值的軌跡是橢圓.

2.？搖探究方程■+y2=1表示什么曲線.

數無形，不直觀！學生討論作圖，猜想方程表示橢圓.

教師：同學們猜想對不對呢？先不要急著下結論，請大家計算一下：

曲線上一點P（x，y）到（1，0），（-1，0）的距離之和有何特點？

學生發現其和為定值.

教師：在前面的實驗中，我們已知道到平面上動點到兩定點距離之和（和值大于兩定點之間的距離）等于定值的軌跡是橢圓，兩定點稱之為橢圓的焦點. 剛才我們的研究發現給定方程上的點滿足這個特點，它確實表示橢圓. 為同學們的發現點贊！老師還有一個問題要問，我們可以解決“圓還是橢圓”的問題了嗎？

學生：可以，利用坐標法建系，寫出方程，判斷曲線類型.

教師：那視頻中的開普勒是在算什么呢？

學生：根據數據檢驗方程是圓還是橢圓. 真可謂坐標一橋飛架，數形天塹變通途！

教師：坐標法可以幫助我們用代數方法研究幾何圖形.

教師：很好！形無數，難入微！老師還有一個問題，請觀察下圖，判斷直線與圓的位置關系.

學生很謹慎，提出需要計算，否則無法準確判斷相切還是相交.

3. 探究y=-x+■，x2+y2=1的位置關系.

學生討論得出可以研究方程組的解的情況，亦可根據圓心到直線的距離判斷，但苦于距離公式不知道，教師鼓勵其想法，指出我們后階段會學習.

變式：y=-x+1，x2+y2=1呢？

學生提出方法類似，教師追問既然相交，弦長可以如何求出呢？

學生：解方程組，得出具體交點坐標，利用兩點距離公式可得.

變式：y=x+1，y=x+2，y=-x+1呢？

教師總結：利用坐標法可以由方程來研究曲線幾何性質、曲線位置關系，計算距離.

（五）核心概念

教師：今天我們學習了坐標法，發現它可以解決很多問題（由曲線上點的特征建立方程，用代數方法研究幾何圖形，由方程研究曲線幾何性質及曲線位置關系），老師卻要問，這方法可靠嗎？

師生討論，理出思維鏈條：

代數方程■方程的解■變量■線段■有序數對■曲線上的點■曲線

其中，思維起點——代數方程;思維指向——代數方程的解;思維跳躍——讓方程的解動起來;思維提取——形可表示數;思維遷移——借助坐標;思維重組——數又可表示形;思維變向——方程可表示曲線;思維反演——曲線與方程統一.

學生總結：建立“曲線與方程”對應的關系很重要，初步認識曲線的方程、方程的曲線的核心概念.

（六）體系建立

解析幾何：一種借助解析式進行圖形研究的幾何學分支，就是把幾何圖形放在坐標系里面加以分析，這樣使得理論更加形象化. 在坐標系里建立點、線、面和各種形狀的解析式，使得表達更加規范.

（七）歷史重現

教師展示數學史微課.

學生：原來前面我們解決的三線軌跡居然是帕普斯軌跡問題的特殊情況，我們和笛卡爾一樣，建立了坐標系，運用坐標法解決了問題，太棒啦！

（八）展望小結

教師：從前面的微課我們知道，解析幾何的創始人之一費馬從方程出發研究曲線. 那我們也利用計算機軟件，展示二元方程（m+1）x2-y2-m（x+1）=0隨參數m值變化，曲線的變化形式.

學生：原來一個二元方程可以統一這么多形式的曲線.

師生總結呈現解析幾何知識樹.

教師：圓、橢圓、雙曲線、拋物線統稱為圓錐曲線. 它在我們的實際生活很重要，許多物體的運動軌跡可以用圓錐曲線或近似地用圓錐曲線表示，很多光學儀器都是利用圓錐曲線（面）的性質制作的. 老師給大家留個課后思考問題，通過初中學習我們知道，形如y=kx+b的方程表示直線，那我們為什么還要繼續研究直線及其方程呢？需要研究什么呢？

學生反饋

通過課前、課后的問卷調查，學生們喜歡數學老師將與數學知識相關的數學歷史、實例融入課堂教學中，喜歡老師在新的模塊或單元學習開始前先帶領他們構建要學的知識框架，明確學習內容和任務，介紹與解析幾何相關的數學歷史對解析幾何學習和理解有幫助，認為以后有必要開設別的章節序言課.

教學感悟

以史為鑒，方能更好地揭示知識的自然發生過程. 本節課中，我們從學生的認知起點出發，以“我們”和“科學家”解決“圓還是橢圓”的問題為抓手，通過問題串，引導學生自然地經歷了坐標法解決幾何問題的過程. 核心問題的探究活動讓學生積極地參與了解決問題的過程，充分地體會了數學探究的樂趣，動手操作不僅獲得了數學活動經驗，提升了數學思維能力，而且激發了數學學習興趣. 數學史微課，更是讓課堂充滿數學文化的芬芳.

現階段在高考升學壓力下，教師過于重視知識點的機械教授，很少在課堂上花很多時間去涉足數學史、數學文化，而且由于教學任務重，課時安排緊，在實際教學中很難擠出時間來上數學序言課. 經過實踐我們發現通過本節序言課，后面在上圓、橢圓、曲線與方程新課時無須再重新引入情境. 此外，學生對距離、位置關系有了探究體驗，對解析幾何整個知識體系有了一定的認識，很好地把握了研究問題的方法，同時讓學生獲得了歷史感，改善了他們的數學觀，提升了他們的數學情感.