構造突破，借“導”探析

董海峰

[摘? 要] 以函數為背景的不等式問題是高中數學的重點問題，其中涉及函數、導數、不等式、方程等知識，對于學生的解題思維有著較高的要求. 解題時采用構造函數法可以把握問題本質，打開突破口. 文章深入剖析構造函數的方法策略，結合實例加以探究，并開展教學反思，提出相應的建議.

[關鍵詞] 不等式;導數;構造;函數;單調性

問題綜述

在近幾年的模考和高考中出現了一類較為特殊的不等式問題，融合抽象函數、導數、不等式等知識，具有較強的綜合性. 同時由于抽象函數的出現，對于學生的解析突破造成了一定的思維障礙，學生難以選擇突破口，不能合理解析不等式問題. 實際上，由于該類不等式問題常以函數為背景，解析時需聯想導函數的分析優勢，構造合適的輔助函數，然后利用導函數的性質來簡化求解. 具體思路是把握不等式的結構特征，結合所求問題構造相應的新函數，然后利用導函數的奇偶性、單調性來解析.

構造探究

“構造函數，借導探析”是突破函數背景下不等式問題的有效策略，而其中關鍵的一步是構造輔助函數. 構造函數的方法有多種，所構函數的特征也不盡相同，掌握構造函數的方法十分重要. 高中階段常用的構建法有很多，大多基于代數運算來構造，如和差、積商，所構函數的形式也較為多樣，如構造具體函數、構造抽象函數、構造“本性”函數，下面結合實例講解問題的構造策略.

1. 構造具體函數

構造具體函數是解析函數不等式的常用方法，“具體函數”，既包括傳統意義上的一次函數、二次函數、指數函數、反比例函數等常規函數，又包括廣義上的有具體形式、確定內容的固定函數. 解析時需要對不等式問題進行恒等變形，從中提取核心內容來構造.

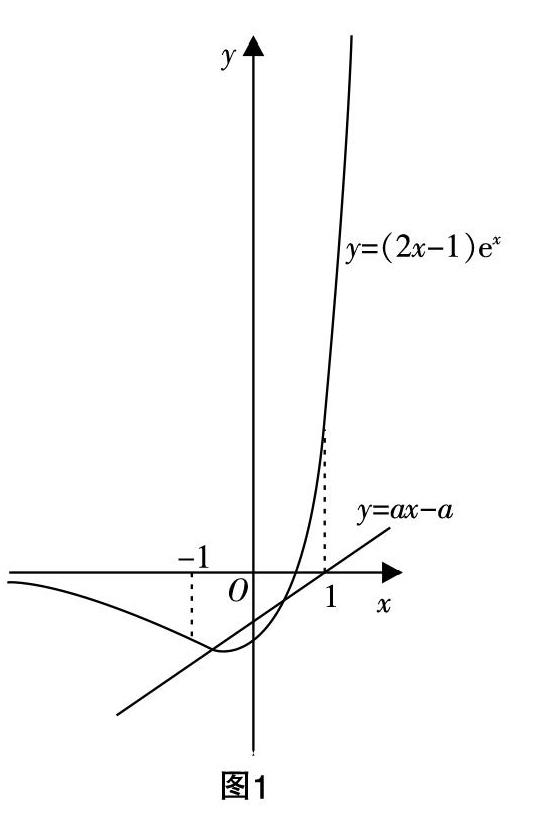
例1：設函數f（x）=2xex+a，g（x）=ex+ax，其中a<1，如若存在唯一的整數x■，使得f（x■）

解析：題干給出了函數f（x）和g（x），并以此為基礎構建了不等式f（x■）

將函數代入不等式f（x）-■時，h′（x）>0，則在區間-∞，-■上，函數h（x）單調遞減，在區間-■，+∞上，函數h（x）單調遞增. 所以x=-■時，函數h（x）取得最小值，且最小值為h-■=-■. 令y=ax-a，則函數h（x）和y=ax-a的圖像如圖1所示，其中h（0）=-1，h（-1）=-■，所以h（-1）

解法指點：對于函數形式確定的不等式問題，可以先通過和差、積商轉化來對不等式恒等變形，然后直接提取不等式內容來構造函數，最后利用導函數的性質來打開解題突破口. 必要時可以借助函數的圖像，使問題變得簡單、直觀，利用數形結合的思想方法解析問題. 而對于較為復雜的復合函數不等式問題，則可以采用先還原、再構造的策略求解.

2. 構造抽象函數

抽象函數是相對于具體函數的一種函數形式，而構造的抽象函數是對原函數不等式性質特征的高度集合. 往往新函數綜合了目標函數的關鍵特點，其中可能含有一些復合函數，可借助所構函數的導數性質開展問題分析.

例2：已知定義在R上的函數f（x）滿足e4（x+1）f（x+2）=f（-x），設f′（x）為函數f（x）的導函數，若對于任意的x≥1均有f′（x）+2f（x）>0，則下列選項一定正確的是（? ? ）

A. e4f（2）>f（0）

B. e3f（3）>f（2）

C. e6f（3）>f（-1）？搖？搖

D. e10f（3）>f（-2）

解析：題干給出了函數f（x）所滿足的條件，以及與其導函數f′（x）之間的不等關系，可以從四個選項中提取、歸納共性，構建相應的特征函數，然后利用對應的導函數來確定函數性質，進而分析選項正誤.

根據選項所涉不等式的特征，設新函數F（x）=e2x·f（x），導函數F′（x）=2e2xf（x）+e2xf′（x）=e2x[2f（x）+f′（x）]. 因為對于任意的x≥1均有f′（x）+2f（x）>0，顯然F′（x）>0，即函數F（x）在[1，+∞）上單調遞增，則有F（x+2）=e2（x+2）·f（x+2），F（-x）=e-2x·f（-x）. 因為e4（x+1）f（x+2）=f（-x），則e2x+4·f（x+2）=e-2x·f（-x），所以F（x+2）=F（-x），則函數F（x）關于x=1對稱，可知F（-2）=F（4）. 根據函數F（x）的單調性可知F（3）F（2），所以e2f（3）>f（2），則選項B正確.

解法指點：上述采用的是典型的構建抽象函數的方法，從選項的函數不等式形式中提取共有特點，然后構建抽象函數. 構造函數可輔助思考問題，降低思維難度，打開解題突破口. 一般抽象函數的構建策略有兩種：（1）根據導函數的“形狀”，從中提取不等式的特征來構造;（2）若為函數不等式選擇題，則可以總結選項中的共性特點來構造函數，如本題所示.

3. 構造“本性”函數

構造“本性”函數，即構造可以反映問題本質內容的函數，因此在構造過程中需要把握問題本質，進行等效轉化，使抽象問題具體化，然后結合不等式內容來構造相應的函數. 總結構造“本性”函數的過程，可以概括為：等效探源，本質構造.

例3：定義在R上函數f（x）滿足條件f（-x）=f（x），且對于任意的不等式實數x■，x■∈[0，+∞）均有■<0. 若關于x的不等式f（2mx-lnx-3）≥2f（3）-f（-2mx+lnx+3）在x∈[1，3]上恒成立，則實數m的取值范圍為____________.

解析：上述同為以函數為背景的不等式問題，根據條件“f（-x）=f（x）”可推知函數f（x）為偶函數，由條件“x■，x■∈[0，+∞）均有■<0”可推知函數f（x）在區間[0，+∞）上單調遞減. 突破的核心是對后續不等式成立的剖析，顯然不適合直接構造函數，需要對函數不等式進行等價轉換，從中獲得反映不等式本質的內容，然后據此構造“本性”函數.

可將f（2mx-lnx-3）≥2f（3）-f（-2mx+lnx+3）轉化為f（2mx-lnx-3）≥f（3）在x∈[1，3]上恒成立，則2mx-lnx-3≤3，即0≤2mx-lnx≤6對于x∈[1，3]恒成立，進一步化簡可得2m≥■且2m≤■對于x∈[1，3]恒成立. 令函數g（x）=■，則導函數g′（x）=■，分析可知g（x）在區間[1，e）上單調遞增，在（e，3]上單調遞減，則g（x）max=■;再令函數h（x）=■，則導函數h′（x）=■<0，所以函數h（x）在區間[1，3]上單調遞減，則有h（x）min=■;所以需滿足2m≥■，且2m≤■，即m∈■，1+■.

解法指點：構造“本性”函數，實則反映的是一種構造解析函數不等式的策略，即等效轉換，特征構造. 與前兩種構造方式最大的不同是在構造之前需對不等式問題進行“本性”挖掘. 運用該種構造方式可以抓住問題本質，化抽象為具體，達到化繁為簡的解題效果.

反思建議

以函數為背景的不等式問題是高中數學的典型問題，通過構造函數，利用函數性質可以簡化問題，高效求解. 上述所探討的函數構造策略也是該類問題常用的構造方法，可以有效挖掘問題本源，降低思維難度，構建直切主體的解析思路. 下面對問題本質及構造方法進行深入反思，提出相應的學習建議.

1. 關于問題構造方法的反思

對于函數不等式問題，其核心是處理不等式關系，但解析的關鍵是聯系函數背景來探究不等式的問題根本，因此“不等關系”是問題的表象，“函數關系”才是問題的本質核心. 在解析問題過程中需要聯合函數背景來剖析不等式，結合已知條件和問題來挖掘不等式與函數的內在聯系，結合構造法構造輔助函數、求解導函數，合理利用函數的單調性、奇偶性和最值來研究不等式. 上述所呈現的三種構造策略，其核心在于把握函數不等式的表象特征、共性特點、內在聯系、本質根源，構造的過程不是改變問題本身，而是借助函數模型來研究性質，利用性質來推理結論.

2. 關于構造函數解題的建議

函數不等式問題具有極強的綜合性，利用構造策略求解問題過程中，除了需要利用構造技巧外，還需要用到函數單調性、奇偶性、不等式性質等知識，上述知識是問題突破的基礎儲備. 在學習過程中需要牢實基礎，把握知識聯系，關注函數與不等式的關聯，為后續基于不等式形式構造函數做基礎. 考慮到構造函數過程需要挖掘不等式問題的特征內涵，教學中建議引導學生合理聯想，發散思維，提升學生的思維品質.