巧借課后習題 助力課堂教學

盧春華

[摘? 要] 課后習題具有鞏固所學知識、開發學生思維等作用. 但在實踐中，部分教師常忽略課后習題的重要性，表現出對待課后習題過于隨意，缺乏關注，不能發揮課后習題的有效價值等弊端. 文章從課后習題對教學思路、概念學習、問題發生與邏輯思維等方面的影響出發，淺析課后習題對初中數學課堂教學的作用.

[關鍵詞] 課后習題;課堂教學;概念;解題

教材中的課后習題是編者綜合教學大綱、課程標準與學生的認知水平等精心編擬而成的，是數學教學中不可或缺的重要組成部分之一，亦是一線教師制定教學目標的可靠依據. 但在教學實踐中，不少教師沒有充分認識到課后習題的重要性，從而忽視了課后習題的導向作用，讓它成為教學過程中的一個擺設. 若教師能將課后習題融合到課堂教學的每一個環節，落實到概念、解題以及學生思維成長等方面，那它將起到鞏固所學內容、提高學生認知水平、拔高思維、提升數學核心素養的重要作用.

關注課后習題，明晰教學思路

初中數學教材的每個單元都設有配套的課后習題，這些習題不但具有考查和鞏固學生的學習情況的作用，還具有為教師的教學指明方向、突出教學重點與難點的作用. 課后習題反映的是編者對教材內容的解釋和暗示，也是教材與教師的一種特殊對話模式. 經過編者精心設計的課后習題，一般是從教學重點與難點入手，以典型習題的形式呈現. 教師在備課時若能抓住課后習題，就是抓住了教學的命脈，明確了課堂教學的目標. 因此，充分發揮課后習題對教學的導向作用，能為教師的教學設計明晰思路.

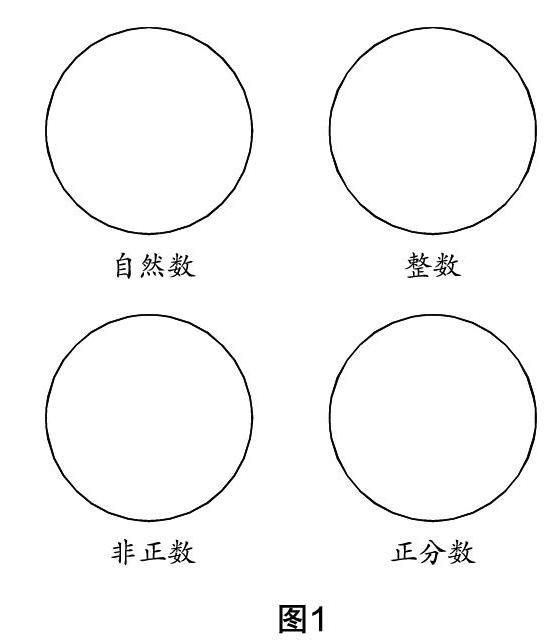
例1?將下列各數填寫到相應的圈（圖1）中：

-1，8，-0.03，■，-43，0，-1■，5.■，9%，13.

教師可借助本題來明晰本章節的教學重點與難點，根據不同標準對有理數進行分類處理. 因此，教學設計時可按照整數和分數來分，再按正負來分，由此理清整個教學思路（如圖2）.

依托課后習題，夯實概念基礎

當前，不少教師認為概念只是寥寥幾行文字，讀讀背背就行了，不需要作為教學的重點，這種現象是教學的重大誤區. 事實上，概念是學習的基礎與前提，不理解概念的學習是徒勞的，解決問題時會因概念模糊而出現各種錯誤. 而課后習題是夯實概念教學的利器，教師通過教學活動的開展進行概念教學，再依托課后習題進行訓練，能有效地提高概念的教學效果.

例2?-2的絕對值是______，絕對值是2的數有________，0的絕對值是________.

“有理數”章節的知識點比較零碎，尤其是絕對值部分，學生在概念掌握上總覺得力不從心. 此時教師可利用課后習題來鞏固各個概念，而不是強制學生機械地誦讀.

-2的絕對值是2，0的絕對值是0，學生很容易理解;絕對值是2的數則出現了兩種情況，這就要求學生對絕對值的概念要理解透徹：所謂絕對值，是指數軸上的一個數，其對應點到原點的距離，常用“”來表示，如2的絕對值為2，-2的絕對值也是2.

教師可通過上述習題進行知識的拓展與延伸. 如問學生：在有理數-1， 1，0中，絕對值最小的是誰？如果x=x，則-x一定是正數、負數或非正數、非負數嗎？學生經過思考與探索后會得到如下結論：正數的絕對值是其本身，0的絕對值是0，負數的絕對值是它的相反數，即a=a（a>0），0（a=0），-a（a<0）.

本題看似簡單，卻考查了學生對絕對值的掌握情況. 教師不能只關注學生填空的結果，而忽視本題對概念教學的價值，應抓住此題的關鍵點，緊扣絕對值的概念，讓學生從習題中獲得基本概念，鞏固概念內容，這樣才能真正把握概念的內涵，為接下來的學習夯實基礎.

借助課后習題，提升解題能力

目前，不少教師將教學的重心放在問題的“巧解”中，而忽略了常規題目的解題過程. 當然，能巧妙地使用便捷的方法解決問題，既省時省力，正確率又高，有事半功倍之功效，但使用便捷的方法解決問題并不具有普遍性，而使用常規方法解決問題才是數學學習的根本. 因此，教師應借助課后習題，發展學生的常規解題能力.

例3?在Rt△ABC中，∠C=90°，BC=12，AC=24，求AB.

不少學生看到此題，直接使用簡化計算方法：將BC的值看作1，將AC的值看作2（同時除以12），先計算出直角邊為1和2的直角三角形的斜邊的值，再用所求的斜邊的值乘12，獲得最終的結論. 但是，這種簡化計算方法并不適用于所有勾股定理的習題，只有運用a2+b2=c2進行計算，才是解決此類問題的關鍵，這也要求學生要掌握數字的乘方、開方計算方法.

相較于便捷的“巧解”方法，常規方法費時費力，特別是數據復雜的情況下，還容易出現運算錯誤. 但是，常規解題辦法卻是永不過時的解題武器，學生只有熟練掌握常規方法后，才能根據習題特征，酌情使用巧解方法. 想要真正地掌握解題思想，只有踏踏實實地在常規解題中不斷地重復訓練，才能有所收獲.

巧用課后習題，暴露常規錯誤

在教與學的過程中，師生常常會產生一個困惑：授課內容已經聽懂了，但是解題時卻出現思維卡殼，找不到解題思路或出現解題錯誤的情況. 究其原因，主要在于教師過于追求教學效率，教學中不自覺地為學生創建了一些思維捷徑，以便學生更快更好地掌握知識點. 而事實卻是事與愿違，學生缺乏自主探索的過程，難以做到知其然，且知其所以然，存在的問題也就在解題過程中得以暴露.

例4?電動車以30 km/h的速度往正北方向行駛，于A處看到路燈O在電動車北偏東30°方向上，電動車行駛2 h后到達B處，看到路燈O在電動車的北偏東45°方向上. 請求出路燈O到B的距離.

在“銳角三角函數”的內容已經學完的基礎上，常會出現如例4與生活實際相關的應用類問題，其中最常見的是運動類問題，學生在解題中常會暴露各種錯誤. 解決本題時，學生暴露的問題主要是不知道用什么基準來確定圖像. 此問題形成的主要因素是，教師在執教時，直接將圖像呈現給學生，學生沒有經歷圖像形成的過程，缺乏探索與思考，導致遇到實際問題時感到茫然而無從下手.

由于課堂時間與空間的局限，導致教師無法在有限的時間內發現教學中存在的漏洞與問題，而課后習題卻具有查漏補缺的功能. 解題需要學生依靠自主分析與思考獨立處理問題，學習中存在的問題也隨著解題而暴露. 因此，教師應關注學生的解題過程，及時發現學生學習中存在的漏洞與錯誤，根據實際情況因勢利導地調整教學方法，查漏補缺，幫助學生完善知識結構.

妙用課后習題，培養邏輯思維

教師在課堂教學過程中常存在一個誤區，那就是對學生的邏輯思維能力掌握得不準確，導致學生跟不上授課進度，進而出現思維被“拖著跑”的現象. 其原因是教師對知識掌握的熟練程度明顯優于學生，教師授課時能根據具體情況迅速做出正確的判斷與思考，而學生處在摸索階段，思維還沒反應過來，教師已進入新的教學環節. 此過程，教師最大的誤區就是忽視了學生的邏輯思維能力水平. 因此，教師可利用課后習題的作用，充分培養學生的思維能力，讓學生在解題過程中逐漸獲得數學思想.

例5?解方程：■-■=1.

“平方根里面的數不小于0”是學生熟記于心的概念，部分教師理所當然地認為解二次根式類的方程，代入驗根是必然的. 但是，不少學生在解這個方程時，卻得到了x1=2，x2=7的結論. 若將結論代入原題檢驗，就會發現錯誤所在，但不少學生卻省略了這一步驟. 這出乎教師的意料. 而從學生的角度來看，只要解出方程，任務就完成了，至于代入驗根這一步卻忘到九霄云外了. 這就要求教師要站在學生的角度，觀察學生的思維走向，并及時引導與糾正，將學生帶到學習的正軌中. 鑒于此，教師在教學中要因材施教地調整教學方法，重點強調一些容易被學生忽視的細節，以促進學生邏輯思維能力的發展.

總之，教師在教學過程中存在的一些誤區，可通過課后習題的訓練，達到明晰教學思路、提高學生解題能力、查漏補缺、提升學生邏輯思維能力的作用. 同時，教師應明確課后習題對教學的指向性，關注學生的解題方法與思維過程，實現以課后習題助力初中數學課堂教學的目標.