“還原法”巧解小學數學應用題
■江蘇省蘇州工業園區第三實驗小學 吳陳軼
數學習題的解答過程中,一般是根據已有的條件進行思考與分析,從中找出解決的方式。我們可以運用一些已知的條件,反向推導,解決這類的數學題型,這種方式被稱之為“還原法”,也稱之為“倒推法”。
一、從“單個對象”著手,按部就班
“單個對象”主要是指在習題中,只有一個主語與總量,并且在解題過程中,即使條件發生變化,但是最后所求解的結論依然是主語與總量。
如,超市售賣一批香蕉,第一天賣掉了總體香蕉的1/2,第二天賣掉剩下的1/2并多售賣出10千克,然后第三天賣掉第二天剩下的1/2并少3千克,這些蘋果最后還剩下10千克,請問這一批香蕉一共有多少千克?在這一道習題里面,“一批香蕉”是其中的主語,也是這道習題中的“單個對象”,因此不管這一批香蕉經歷幾天的販賣,都需要解答“一批香蕉”是多少千克。在面對這樣的習題中,為方便理解,一般都需要建立流程圖、還原圖或者倒退圖,對這三種圖像中的一種進行分析。這三種方法的選用中,需要根據班級學生的數學水平,確切地選擇方式,以下將論述其中的一種方式。
所運用的方法為流程圖方法。首先,需要做出其中的流程圖,即圖1。流程圖的繪畫較為簡單,只需要根據習題內容進行繪畫,如,將每天店中剩下的香蕉用空格表示,并在箭頭上標注好每天售賣的量,流程圖的繪畫就完成了。計算也較簡單,只需要向前推導即可,但是要注意在推導過程中變化符號。在流程圖的繪畫中,學生大多會發生以下兩種錯誤。第一,對于在繪畫箭頭上的標注中,對于“多賣出10千克”“少2千克”的符號運用出現錯誤,這是就需要他們對于習題與流程圖中各種知識點都有明確的認知,明白空格是店內所剩的香蕉質量,從而理解所需什么符號。第二就是計算中所出現的錯誤,在進行計算時,是需要進行反向計算,因此在計算時,需要對符號進行修改,如,箭頭上的減法,計算時需要修改成加法等。或者在計算時,對于計算的順序發生錯誤,在進行反向計算時需要反向推導,因此在列式時需要添加一定的括號,防止計算順序的錯誤,對其進行計算有所幫助。

圖1流程圖
二、從“多個對象”出發,靈活運用
“多個對象”其中主要是指:在習題中,會有多個主語在其中,并且在計算過程中,多個主語也會同時出現變化,但是在最后所求得的依然會是這些多個主語或者這些多個主語的部分。例如,在三輛公交車上,有48個人乘坐前往同一個地方,但是每輛車上的人數不等,因為部分原因需要平衡人數,因此從第一輛車中下來6人到第二輛車中,之后在第二輛車中下來8人到第三輛車中,從而車中人數平衡了,請問原來三輛車中分別有多少人?
在這道習題中,主要有三個主語對象,即在剛開始時三輛車上的人數,在習題中這三輛車上的人數都在發生變化,最后達到一致的數目。因此,在學生初次接觸這類習題中,都難以直接進行解決,主要是因為在其中涉及多個主語,并且其中的數量還在不斷變化,這就需要教師進行一定的引導。對于上一習題主要可以繪畫出以下的示意圖,如圖2。
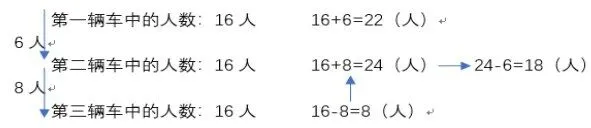
圖2車輛中人員的調動
通過圖2,不難發現在最后每輛車中的人數相同,因此最后每輛車中都會有16人,因此,一次推導,通過“之后在第二輛車中下來8人到第三輛車中”這句話可以推導出,在這次人員調動之前,第三輛車只有8人,第二輛車有24人。最后,再根據“因此從第一輛車中下來6人到第二輛車中”這句話得出,最開始第一輛車有22人,第二輛車有18人。通過逐次推導的方式得出結論,在這種類型題的解決中,學生主要需要注意兩點,首先,在建立示意圖后,直接根據數量關系和習題中的話語,反向推導。最后就是需要注意其中的數量關系,注意其中的各種符號運用。
三、以“不同對象”分析,確定核心
“不同對象”同樣是指多個主語,但是“不同對象”的多個主語與“多個對象”的多個主語不同,“多個對象”的多個主語一般是指同種的事物,而“不同對象”的多個主語是指不同的事物,并通過反向推導的方式推導出“不同對象”的答案。例如,在商場引進一批香蕉進行售賣,最開始進行稱重,香蕉與筐一共重104斤,通過一天的努力,上午售賣出一半的香蕉,下午也售賣出了上午所剩下的一半,最后再進行稱重,香蕉和筐一共重29斤,問香蕉多重?筐多重?在學生進行分析中,如果未注意,就會根據“多個對象”的習題方法進行解答,但是在這道習題中,需要注意筐與香蕉是不同性質的物質,并且筐的質量一直未發生變化,香蕉的質量發生了變化,所以解答的方法就不同。介紹一種解答方式,如下:將其中的香蕉設置成一個未知數,先求解香蕉的質量,首先因為“最開始進行稱重,香蕉與筐子一共重104斤”與“最后在進行稱重,香蕉和筐一共重29斤”兩句話,推導出一天一共售賣出了75斤,并且通過“上午售賣出一半的香蕉,下午也售賣出了上午所剩下的一半”可以看出售賣的75斤也是香蕉總量的3/4,通過計算得出香蕉的質量為100斤,再計算一下得出筐的質量為4斤。在這道習題的解決方式運用的主要為份數與比例法進行還原計算,在數學學習中所經常使用的方式。
四、讓“相同對象”一致,加深印象
“相同對象”的特質與“單個對象”一致,在題干中主語以及總量相同,其所求的未知量與主語一致。例如:某水果店購入一批水果,第一天賣出的水果量比總量的一半少10斤,第二天賣出的水果比剩下的水果的一半多8斤,現在的水果量為20斤,問:這家水果店原本購入多少斤水果?從題干看,主語是這批水果,所求也是水果總量。針對此類題目,我們可以讓學生先算出水果店原本購入的水果量[(20+8)×2-10]×2=92斤。當算出水果總量后,要學生進行檢驗,即用“還原法”進行反推:(92÷2+10)÷2-8=20斤。我們利用“逆向思維”進行推導檢驗,一方面可以檢驗此題正確與否,另一方面還能加深學生運用還原法檢驗此類題目的效果,提升了學生的解題效率。
五、結語
遇到上文所列舉的問題時,可運用“還原法”解決小學數學中的這類題型,讓題目變得簡單、明了,提升小學生此類題型的解題效率。

