基于數列極限教學內容的變革與實踐

程小靜

(陜西理工大學，陜西 漢中 723099)

極限貫穿高等數學內容的始終，其中數列極限[1]是初學高等數學最難理解而又重要的問題之一，是學生從初等數學到高等數學不得不跨越的門檻，因此，很多課堂創新、教學模式變革[2]的探索都以數列極限為例，因此，數列極限非常重要，相對于數列極限無窮小數列就容易理解多了。本文針對這一教學重難點采取首先引入無窮小數列的定義與性質，再由無窮小數列的定義給出數列極限的定義，結合無窮小數列的性質討論數列極限的性質，來分散難點，是對高等數學內容嘗試的一種新的教學模式和變革。

1 無窮小數列的定義和性質

1.1 無窮小數列的定義

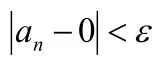
②關于ε：具有二重性，即任意性、相對固定性。

③關于N：特定的項數與ε有關。

⑥無窮小數列的幾何意義：任給ε>0，總能找到正整數N，使從第N+1項開始中的所有項都落在0的ε領域內，這表明無窮小數列從某項起越來越密集在0的任意鄰近，而在這鄰域之外至多有N項：(見圖1)。

圖1 無窮小數列的幾何意義

1.2 無窮小數列的性質

1.2.1 無窮小數列必有界

首先，說明數列有界性的定義。

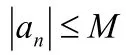
其次，證明性質無窮小數列必有界。

1.2.2 有限個無窮小數列的和、差、積仍為無窮小數列

以兩個無窮小數列的和仍為無窮小數列為例證明.

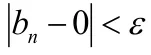
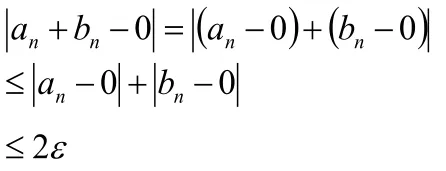
1.2.3 常數或有界數列與無窮小數列的乘積仍為無窮小數列

以有界數列與無窮小數列的乘積仍為無窮小數列為例證明。

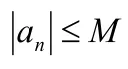
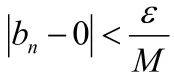
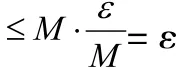
說明有界數列與無窮小數列的乘積仍為無窮小數列，常數與無窮小數列的乘積仍為無窮小數列類似證明。

2 數列極限的定義和性質

2.1 數列極限的定義

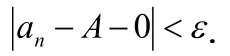
②關于ε，N同無窮小數列定義中的相同。

④數列極限的幾何意義。這里借助無窮小數列定義的幾何意義完全可以嘗試讓學生自己總結數列極限的幾何意義，注意強調數列極限存在與否同樣與數列的前有限項無關。

2.2 數列極限的性質

2.2.1 收斂數列的極限是唯一的

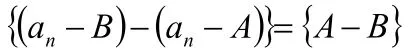
為無窮小數列，說明A=B故收斂數列的極限是唯一的。

2.2.2 收斂數列是有界的

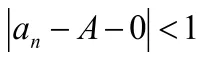
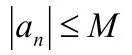
3 解決數列極限實際教學中存在的困難

盡管對于數列的研究大多是通過算式來表述的，但算式的表述在教學中有時并不能非常地直觀說明數列的性質，所以，需要借助文字來描述數列極限，在教學中做到使學生可以深入認知數列極限，讓學生觀察數列動圖，以求對數列進行定性描述。

如果用語言描述的方法概括數列極限現象，得到：

對于數列極限的描述都是從已知到未知進行的，在這一過程中伴隨著簡單到復雜的現象。在教學實踐過程中，盡管數列極限對于學生來說是一個全新的概念，但在描述數列極限過程中運用到的絕對者不等式卻在較早以前的學習中就有涉及到，并不復雜。絕對值不等式的表示在數列極限中是一個關鍵的因素，可以認為，數列極限事實上就是初級絕對值不等式的實際應用。為排除學生在學習數列極限過程中的困難，可以帶領其去認知數列極限和ε-N的演變過程，所以，在教學實踐過程中定義數列極限大致可分為四步，即將數列極限教學分為幾個分步驟進行，在教學過程中教師不應該直接給出數列極限的定義，而是通過每一個步驟與學生共同探索。

3.1 對數列的特點進行觀察

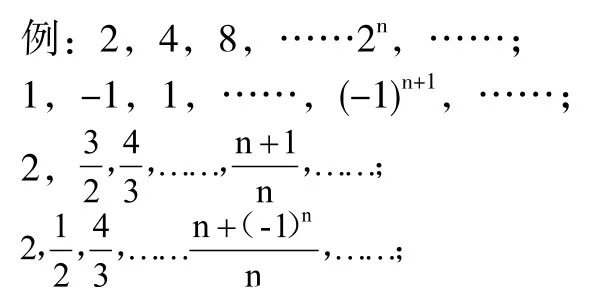
在向學生示例上述算式以后，開始引導其從前所學過的數列知識，最早的數列學習可以回溯到初中數學，但初中數學中的數列學習只涉及到數列的首項、尾項、項數，為初級的等差數列、等比數列等。而在本次學習的數列極限中，更關注的是數列的變化趨勢，通過這樣的引導使學生主動發現一些數列極限的規律，對于數列知識較為扎實的學生來說，可以很容易發現有的數列極限存在越來越大的變化趨勢，有的數列極限處于擺動狀態，而有的數列存在趨近于某一常數的現象。為更加直觀地引導學生繼續分析，教師可以通過數軸將數列標注出來，同時，教師需要對學生發現的規律進行及時地總結概括：部分數列存在一致的現象，例如，隨著n的數值不斷增加，數值會與常數1越來越接近，此時學生會意識到數列極限的這種現象與曾經學習過的函數單調性、函數奇偶性、函數周期性極為相似，將數列極限與函數性質進行對比，可以發現隨著n的無限增大，數列值會與某一常數無限接近。

3.2 引用學過知識并及時予以糾正

教師需要糾正學生在數列極限中不可以用“無限增大”“無限接近”等非專業用語，再一次引導學生回憶初中數學中的函數單調性，對于函數單調性的描述為“隨著自變量的變化，函數值也隨之變化”，在高中數學中，將函數值的變化描述轉化為數學語言，即定義區域內的某區間任意點x1，x2，若x1＜x2，則存在f(x1)＜f(x2)或f(x1)＞f(x2)，即將定義過程進行直觀描述。由此可以做出如下定義：對于數列和常數A，任意指定正數ε，終有一個時刻恒成立。

3.3 證明數列極限

3.4 深化概念

前三步對于數列極限的定義還僅局限于概念層面，為使學生可以更進一步地了解數列極限的本質屬性，需要通過以下幾方面強化學生的數列極限認知：

(2)在進行數列極限解析過程中，要求教師重點分析定義中的關鍵詞，并使學生清楚了解定義中每個字在定義中的意義，尤其要重點解釋ε的雙重性、絕對值的穩定性或相對穩定性，以及N對于ε的依賴性。

(3)教師還可以通過變式教學清楚地表示數列極限的個本質屬性，同時，配合數列舉例，再配合沒有極限的發散例子，以反襯的方式通過非本質屬性表現數列極限的本質屬性，使學生更加清晰、形象地了解數列極限的本質屬性，加深印象。

4 結論

通過引入無窮小數列的定義和性質為數列極限提供了一個新的教學模式與思路，通過具體的無窮小數列引導學生深刻理解任意小正數，進而理解任意小正數與正整數的依賴關系。甚至利用無窮小數列學生可以自己總結數列極限定義的幾何意義，完全可以嘗試利用無窮小數列的性質來證明數列極限的性質。這一新的教學模式不但使學生更容易掌握數列極限的深層內涵，增加師生間的雙向互動，而且對于強化學生自身學習能力，增加學生學習高等數學的興趣，都是傳統教學內容無法比較的。