基于ARMA模型對財政收入的實證研究分析

文| 王馨怡

財政是政府為滿足社會條件的需要而發行的社會產品。隨著經濟的高水平發展，社會產品的生產量將增加，財政收入也將相應增加。財政收入在實現國家宏觀調控和優化資源配置中發揮著重要作用。以適應經濟發展需要，保持經濟社會穩定協調發展。近年來，中國經濟發展水平不斷提高，財政收入也保持了快速增長的態勢。

財政收入占國內生產總值(GDP)的比重不斷提高，財政收入增長與經濟增長之間的互動關系成為一個值得關注的問題。本文選取2008年1季度至2019年3季度的財政收入的數據，采用ARMA模型對未來47個季度的財政收入對經濟發展影響進行分析。

ARMA模型的構建

輸入數據檢驗序列是否符合白噪聲即是否平穩，之后再計算ACF、PACF發現并不在低階結尾，因此我們選用ARMA模型。

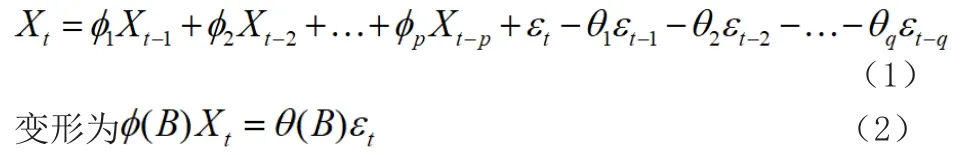
數據的檢驗與分析

平穩性檢驗

導入財政收入2008年1季度到2019年3季度的對數收益率數據，得到對數時序圖，如下圖所示。

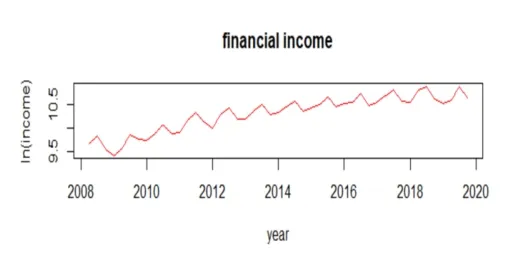
圖1

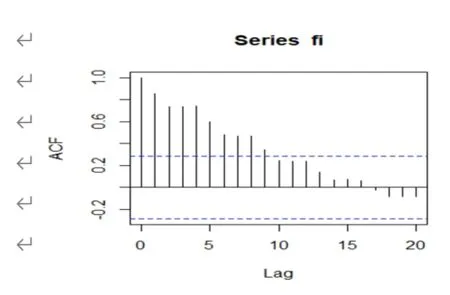
圖2

圖1顯示，從2010年-2019年總體呈上漲趨勢并且伴有規律的波動，其中，第1季度和第3季度對數較小，呈下降趨勢；第2季度和第4季度整體呈上升趨勢，說明該對數具有高度的樣本序列相關性和季節性。進一步分析ACF自相關，得到圖2，該圖證實了該數據卻具有很強的序列性和弱平穩性。

平穩化處理

我們首先對財政收對數數據進行差分，因為差分前幾項出現負值，我們采用滯后階數對其進行差分，得到：

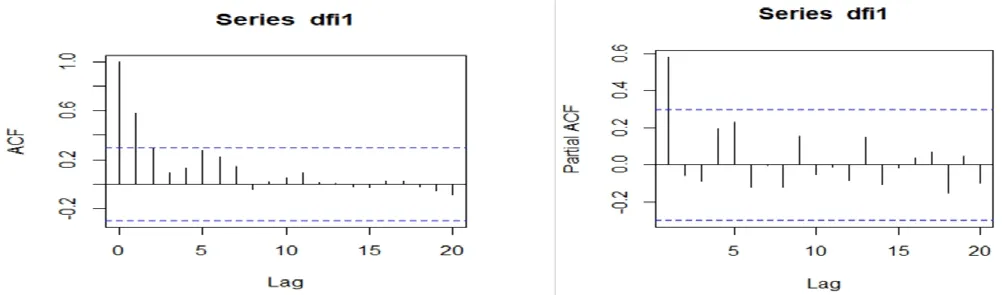
圖3 差分后的對數序列的ACF、PACF

再進一步進行白噪聲檢驗后發現，P值為8.32e-5,檢驗結果中P值小于5%，說明該序列通過平穩性檢驗。

模型的實證分析

建立模型

首先，根據對數序列的ACF建立AR（2）模型，通過比較兩種模型，選出最佳的模型。

1.建立的AR（2）模型M1：

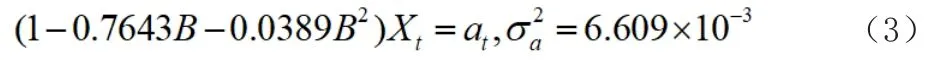
結果顯示均值為0.0901，數值太小，因此將均值去掉；同時發現二階時滯過小，移除后，建立AR（1）模型M2：

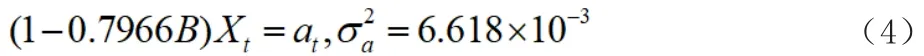
進行殘差檢驗發現，M2模型的ACF在滯后5階有一個顯著非零，標準化殘差仍有異常值。因此嘗試ARMA(2,5)。第三次白噪聲測試不顯著，表明原始假設滿足白噪聲要求。

2.將數據代入，建立ARMA（1,5）模型M3：

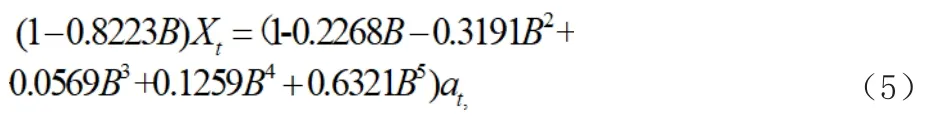
因為MA模型中，3、4階不顯著，我們將MA的3、4階去掉，得到模型M4：

再次進行殘差檢測發現，標準化殘差較M1模型變小。AR(1,5)殘差的自相關基本通過白噪聲檢驗。其中各個白噪聲檢驗均不顯著，說明原假設為符合白噪聲要求。

模型的比較與選擇

表1顯示，M4模型比M1、M2、M3模型的AIC更小一些，并且標準差略大，因此選用M4模型。

?

模型的預測

根據建模步驟，對M4模型進行前5步預測，以5%為預測區間的置信水平，并對模型產生的預測誤差進行了檢驗。白噪聲測試用于檢測延遲為1-20階時，樣本中的預測誤差是否為非零自相關

檢驗結果為：X2=8.6824，df=20，p-value=0.9863

因此，殘差具有良好獨立性，檢驗通過，預測成立。繼續推測未來5季度的預測值，其相對誤差也均在7%左右波動。但具體誤差為多大，需要與2019年第四季度以后的五個季度的實際對數值進行比較才得知。

圖4顯示，未來5季度財政收入可能略微下降，與我國政策和經濟調控的大方向有關，財政收入可能對經濟總量也造成一定影響。

結論

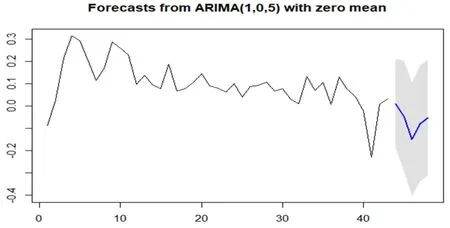
圖4 預測圖

本文對財政收入對數進行平穩性分析，將原始數據進行平穩化差分處理，使用ACF和PACF觀察其平穩性，基本合理后開始建模。

預測選取最優M4模型，主要分以下兩個部分：（1）僅預測五個值，目的是方便與接下來的短時間內幾個季度的數據做比較，從而在更短時間內證明該模型的可行性。（2）對預測值的殘差進行檢驗，判斷預測是否成立，若不成立則要進一步對殘差進行建模分析，再選擇平穩模型，對該模型進行預測。