深度教學，提升三角函數解題能力

江蘇省淮陰中學 顏 艷

一、公式變形，梳理基本關系

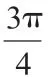
對于公式變形的要求首先是要熟練準確地把握基礎公式，進而引導學生結合題目信息巧用公式，熟悉公式的逆用及其變形。教師要加強訓練，促使學生熟能生巧，實現公式的嫻熟與靈活運用。

二、數形結合，確定取值范圍

數形結合是學生在解三角函數題時必須掌握的思路和能力，利用數形結合的思想可以幫助學生將抽象的題目表征形象化，通過結合題目表述畫出圖形，根據圖像直觀清晰地進行分析，理解題意，優化解題途徑。

例如，在求取值范圍的題目中就非常需要作出三角函數的圖像來幫助解題。以一個簡單的例題來講：函數f(x)=sinx+2sinx，x 在[0,2π]的圖像與直線y=k 有2 個不同的交點，要求k 的取值范圍。首先，根據三角函數的解析式f(x)=sinx+2sinx 先畫出函數圖像，這時我們很明顯地可以看出函數由兩部分組成，x 在[0,π]上時，f(x)=3sinx，0 ≤f(x)≤3；x 在[π,2π]上時，f(x)=-sinx，0 ≤f(x)≤1。再結合直線y=k 與函數f(x)的圖像有2 個不同的交點，通過圖像我們可以直觀地得出直線y=k 只有在1

數形結合的思想是處理三角函數問題的重要方法，教師要逐步引導學生能夠樹立胸中有圖、見數想圖的思想意識，從而“以形助數”，深化學生的解題能力和數學思維能力。

三、多元轉換，考慮周期因素

在三角函數中，我們學習的正弦函數、余弦函數等的定義域都是實數集R。具體解題時，教師要引導學生結合三角函數的周期性，實現局部和整體間的轉化，充分考慮和利用函數的周期性幫助我們快速、簡便答題。

教師要在三角函數的性質和基本公式的基礎上進一步深度教學，總結解題方法，幫助學生深層次學習和理解三角函數的內容。

教師要在教學過程中不斷摸索新的教學方式和解題技巧，深度教學，讓學生能選擇出題目的最優解法，打開解題思路，總結答題規律，縮短解題所用的時間，提升三角函數解題能力，真正幫助學生攻克三角函數這個大難題。