基于多元線性回歸的學生成績分析?

張 曉 李曉戈

（西安郵電大學計算機學院 西安 710121）

1 引言

在互聯網+時代，我國高校的辦學規模不斷擴大［1］，高校的信息化建設也在逐步完善。與此同時隨著數據挖掘技術的深層次應用，數據挖掘技術也逐漸應用到高校教學管理中［2］。高校招生規模日益擴大，傳統教學管理模式面臨巨大的挑戰，在轉型高校中的體現愈發明顯。高校的教學管理系統在高校的教學管理中發揮著越來越重要的作用［3］。但是目前的教務管理系統只是實現了數據的存儲、查詢、統計等功能［4］，沒有進一步挖掘數據中有價值的信息。以我校的學生成績管理系統為例，該系統只實現了對學生成績的簡單查詢和數理統計，利用這種方法得到的數據只是計算機技術的簡單應用，無法發現影響學生成績的具體因素［5］，以及各種因素之間的關系。如何有效地分析以往的學生成績數據，從中挖掘潛在的學生成績的影響因素［6］，不斷提高高校的教學質量，成為所有高校教學管理的核心內容。

本文首先利用數據挖掘軟件Weka［7］對榆林學院信息工程學院2003～2015 學年計算機科學與技術專業的722 名學生成績進行關聯規則分析，猜想課程之間是否存在關聯性，企圖能找出學生所學習的課程之間存在的一些關聯規則；然后利用數據挖掘軟件Wake 對榆林學院信息工程學院2003～2015學年計算機科學與技術專業的722 名學生成績進行多元線性回歸分析，猜想基礎課程對與之相關的專業課是否會產生影響，企圖能找出學生所學習的基礎課程對與之相關的專業課會產生怎樣的影響。

2 數據與方法

2.1 數據

本文的研究數據來源于榆林學院教務管理系統，并與學校管理者簽訂了保密協議，原始數據是榆林學院信息工程學院2003～2015 學年的學生成績，本次數據的預處理是通過Microsoft Excel2010除去科目中的公共選修課和某些公共必修課，本次數據中未發現空值。

利用數據挖掘軟件Wake對學生成績進行關聯規則挖掘和多元線性回歸分析，從原始數據中選出計算機科學與技術專業2003～2015 學年所學習的五門基礎課和七門專業課共十二門課程：五門基礎課分別是C 語言程序設計、大學英語、高等數學、大學物理和線性代數，并分別用A、B、C、D 和E 表示；七門專業課分別是操作系統、匯編語言程序設計、計算機網絡、計算機組成原理、離散數學、數據結構和數據庫原理，并分別用F、G、H、I、J、K 和L 表示，在表1中列出。

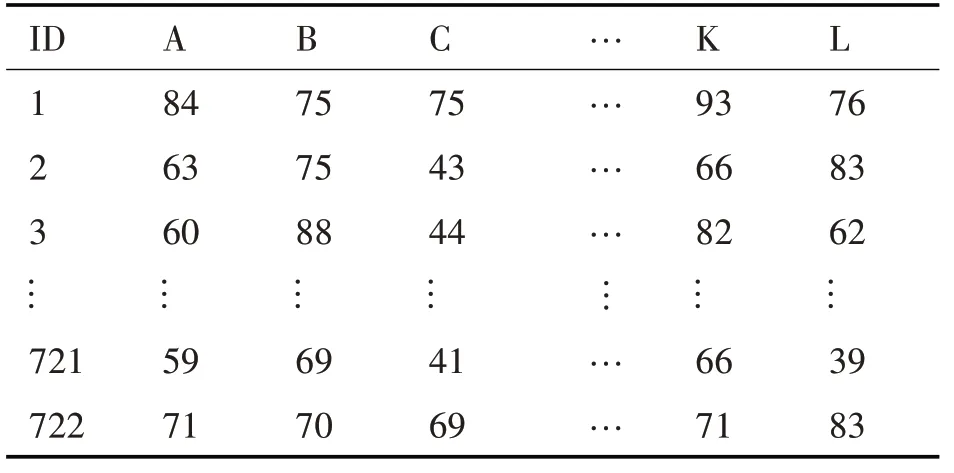
表1 十二門課程的學生成績

關聯規則挖掘必須要將被研究的數據進行離散化［8］處理，對研究數據進行手動離散化和概念分層［9］。首先，將十二門課程的學生成績分成三段，分別是0～60 分，60～80 分，80～100 分，并進行分段標記。以C 語言程序設計為例，C 語言程序設計0～60 分，60～80 分，80～100 分分別標記為A3，A2，A1。在進行手動離散化和概念分層之后的數據，在表2中列出。

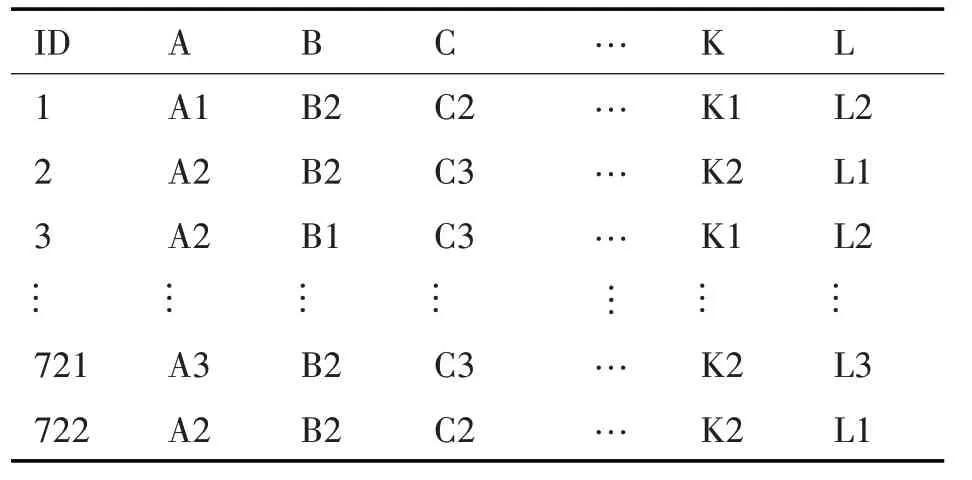
表2 對十二門課程進行離散化和概念分層

利用多元線性回歸分析，挖掘基礎課程對專業課程是否會產生影響。將五門基礎課與其中一門專業課的數據多元線性回歸分析，以匯編語言程序設計為例，即篩選出C 語言程序設計、大學英語、高等數學、大學物理、線性代數和匯編語言程序設計，在表3中列出。

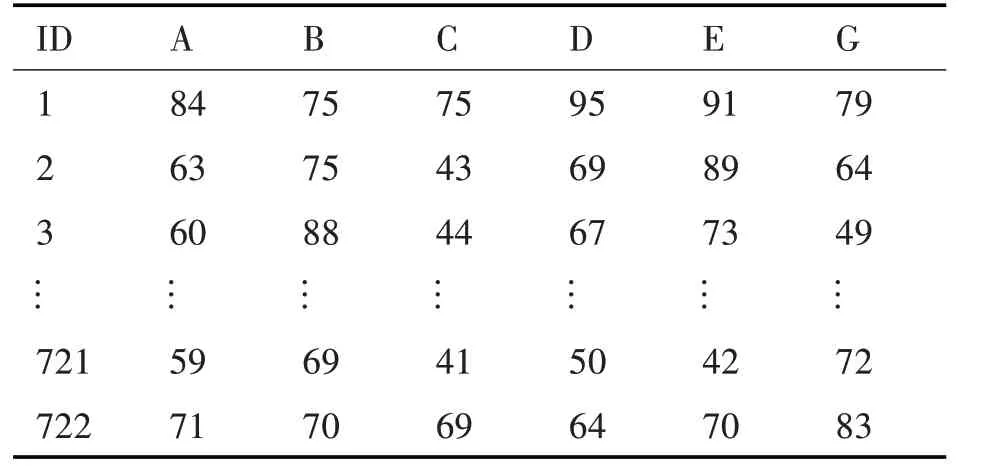
表3 基礎課和匯編語言程序的成績

2.2 方法

2.2.1 關聯規則介紹

關聯規則挖掘是發現大量數據中項集之間有趣關聯或相關聯系［10］。實現關聯的技術主要是統計學中的支持度和置信度分析［11］，支持度主要用于測量連接分析中的統計在數據集中的重要性，置信度用于測量連接分析中的可信度［12］。支持度即在事物集U中不僅出現項集A又出現項集B的事務為a%，則關聯規則A==＞B 的支持度為a%，即表示A和B在事務U中出現的頻率，式（1）列出

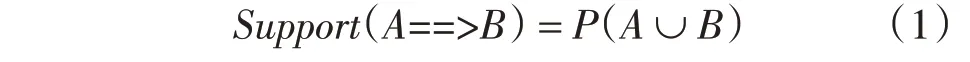
置信度即在事務U中出現項集A的同時項集B也出現的概率，表示關聯規則的強度，式（2），式（3）列出

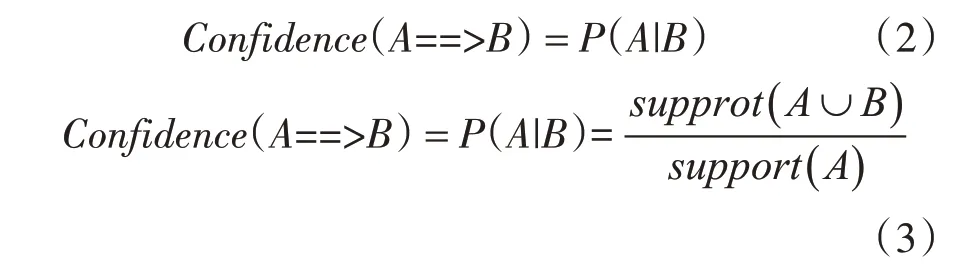
關聯規則的算法有很多，本文主要采用的是關聯規則的經典算法Apriori算法［13］，該算法使用一種逐層搜索的迭代方法：N 項集用于搜索（N+1）項集。首先，找到頻繁1 項集的集合，記作M1，M1 用于找到頻繁2 項集的M2，而M2 用于找到M3，如此下去，直到不能找到頻繁N 項集，每一次搜索都需要掃描一次數據庫，為提高頻繁項集逐層產生的效率，一般作法是利用Apriori 算法的性質壓縮收縮空間［13］。Apriori 算法的性質是頻繁項集的所有非空子集必須也是頻繁的。

2.2.2 多元線性回歸介紹

回歸分析是從一組數據出發通過一個或一些變量的變化解釋另一個變量的變化［14］。首先根據對實際問題的分析判斷，將變量分為解釋變量和非解釋變量；其次，根據函數擬合方式，確定合適的數學模型來描述變量間的關系，再在統計擬合的準則下確定模型的參數，建立回歸方程。由于涉及到的變量是不確定的，回歸方程是在樣本數據的基礎上得出，必須進行回歸模型的統計檢驗，經統計檢驗后，再根據回歸模型，進行因變量的預測。

回歸分析的類型分為一元線性回歸和多元線性回歸，本文主要采用的是多元線性回歸。多元線性回歸的基本模型

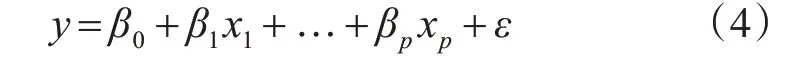
其中x1，x2，…，xp是自變量，β0，β1，…，βp是未知參數，ε是零均值隨機變量。

如果對式（4）兩邊求期望，則有多元線性回歸方程

估計未知參數β0，β1，…，βp是多元線性回歸分析的核心任務之一。由于參數估計的工作是基于樣本數據的，由此得到的參數只是參數真值的估計值，記為，，…，。最終解得模型（4）的多元經驗回歸方程

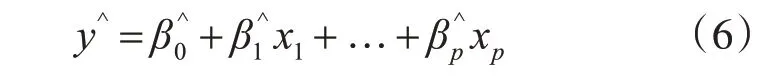
多元回歸模型中的檢驗有兩種，一種是回歸系數的顯著性檢驗，即是檢驗某個變量xi的系數是否為零；另一種檢驗就是回歸方程的顯著性檢驗［15］，即是檢驗改組數據是否使用于線性方程做回歸。

3 基于數據挖掘技術的學生成績分析

3.1 利用關聯規則挖掘對學生成績的挖掘結果

將已經過離散化和概念分層的數據在挖掘軟件Wake 使用Apriori 算法進行訓練，在訓練中不斷調整參數設置，其中classIndex 是類屬性索引，delta是迭代遞減單位，LowerMinSup 指的是最小支持度下界，MinMetric 指的是度量的最小值，SigLevel 指的是重要程度，進行重要性測試，upperMinSup指的是最小支持度上界，最終參數修改結果在表4 中列出。

表4 關聯規則挖掘參數設置

最終得到榆林學院信息工程學院計算機科學與技術專業所學課程中的十二門課程之間的關聯規則，在表5中列出。

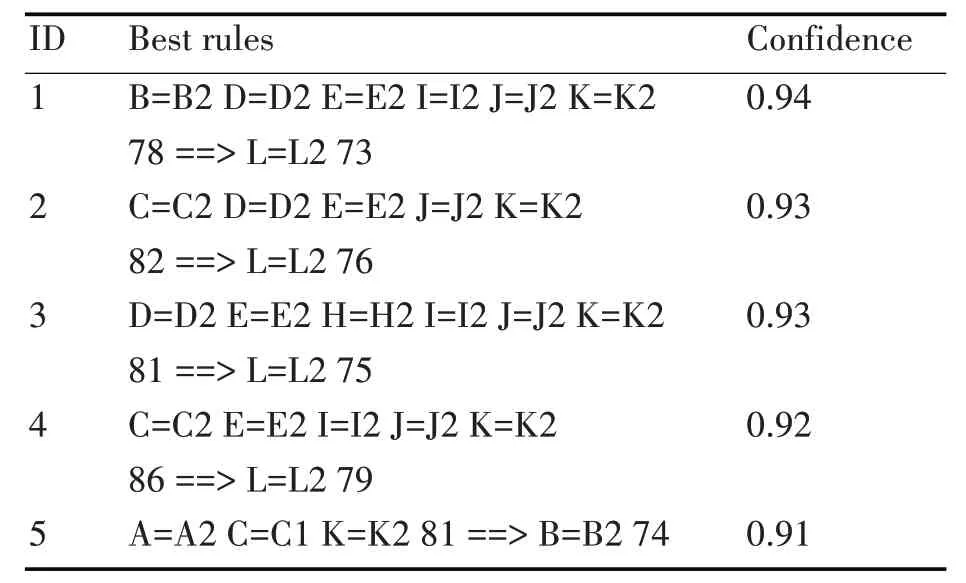
表5 關聯規則挖掘結果

通過對十二門課程進行關聯規則挖掘得到的規則分析有：1）如果大學英語、大學物理、線性代數、計算機組成原理、離散數學、數據結構的成績均在60～80 分之間，那么數據庫原理的成績在60～80分之間有94%的可能性；2）如果高等數學、大學物理、線性代數、離散數學、數據結構的成績均在60-80 分之間，那么數據庫原理的成績在60～80 分之間有93%的可能性；3）如果大學物理、線性代數、計算機網絡、計算機組成原理、離散數學、離散數學數據結構的成績均在60～80 分之間，那么數據庫原理的成績在60～80 分之間有93%的可能性；4）如果高等數學、線性代數、計算機組成原理、離散數學、數據結構的成績均在60～80 分之間，那么數據庫原理的成績在60～80 分之間有92%的可能性；5）如果C 語言程序設計、高等數學、數據結構的成績均在60～80 分之間，那么大學英語的成績在60～80 分之間有91%的可能性。

綜上所述，數據庫原理的成績與大學英語、高等數學、大學物理、線性代數、計算機網絡、計算機組成原理、離散數學和數據結構的成績有關系；大學英語的成績與C 語言程序設計、大學英語、高等數學、計算機網絡、計算機組成原理和數據結構的成績有關系。

3.2 利用多元線性回歸分析對學生成績的挖掘結果

將研究數據在Wake 中選擇Linear Regression算法，使用默認參數，選擇Cross-validation，設置Folds 為20，即使用其中的20 條數據進行交叉驗證。并分別對F列、G列、H列、I列、J列、K列和L列的數據進行預測。

根據上述對多元線性回歸建立回歸模型的分析，可對本次研究的數據建立模型：

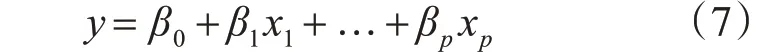
其中自變量x1、x2、x3、x4和x5分別代表C 語言程序設計、大學英語、高等數學、大學物理和線性代數，因變量y1、y2、y3、y4、y5、y6和y7分別代表操作系統、匯編語言程序設計、計算機網絡、計算機組成原理、離散數學、數據結構和數據庫原理。預測的多元線性回歸模型在表6中列出。

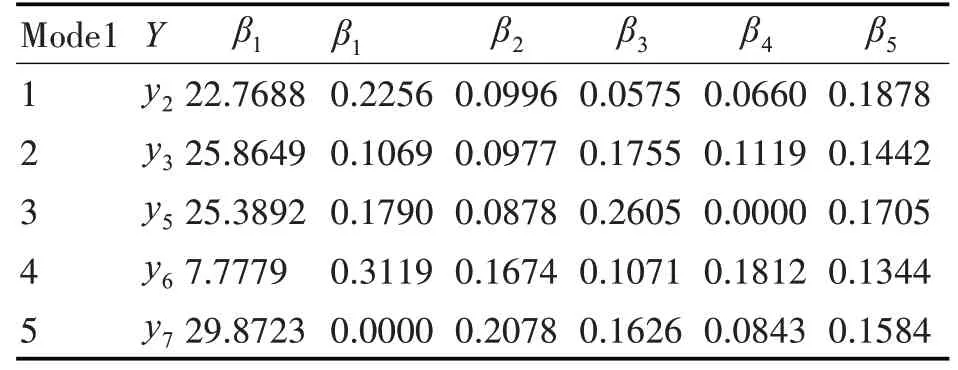
表6 多元線性回歸模型

回歸模型的好壞由模型評價參數來說明，R、MAE、RMSE、RAE 和RRSE 分別代表的是相關系數、平均絕對誤差、均方根誤差、相對誤差絕對值和根相對誤差，模型評價參數在表7中列出。

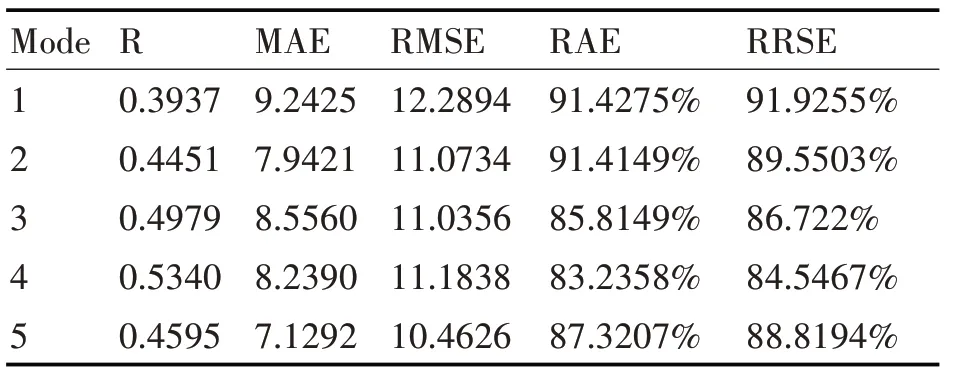
表7 回歸模型評價參數

針對線性回歸模型與回歸模型性能指標，可得到結果有：1）匯編語言程序設計會受到基礎課程C語言程序設計、線性代數、大學英語、大學物理和高等數學的影響，其中對其影響較大的基礎課程是C語言程序設計和線性代數；2）計算機網絡會受到基礎課程高等數學、線性代數、大學物理、C 語言程序設計、和大學英語的影響，其中影響較大的基礎課程是高等數學和線性代數；3）離散數學會受到基礎高等數學、C 語言程序設計、線性代數和大學英語的影響，其中影響較大的基礎課程是高等數學和C語言程序設計；4）數據結構會受到基礎課程C 語言程序設計、大學物理、大學英語、線性代數和高等數學的影響，其中影響較大的基礎課程是C 語言程序設計和大學物理；5）數據庫原理會受到基礎課程大學英語、高等數學、線性代數和大學物理，其中影響較大的基礎課程是大學英語和高等數學。

綜上所述，數學類專業課受數學類基礎課的影響較大，比如高等數學對離散數學的影響就很大；計算機類專業課受計算機類基礎課的影響較大，比如C 語言程序設計對匯編語言程序設計的影響就很大；計算機類和數學類相結合的課程會同時受計算機類和數學類基礎課的影響，比如C 語言程序設計和線性代數對操作系統的影響就很大。

4 結語

本文主要通過數據挖掘軟件Wake對學生成績進行了關聯規則挖掘和多元線性回歸建模，并給出了參數設置和模型評價參數，分別得到了課程與課程之間的關聯和基礎課程對專業課程的影響。基于數據挖掘技術的學生成績分析是一個比較廣泛的課題，在利用關聯規則挖掘學生成績時，只是對課程之間的相關性進行了分析，沒有加入一些附加因素，比如，學生的性別、年齡、年級和英語等級考試成績等學生基本信息。在利用多元線性回歸對學生成績建立回歸模型時，只是分析了基礎課程對專業課程的影響，沒有建立學生平時成績對考研成績的回歸模型。以上這些不足之處將會在下一步的研究工作中得到完善與優化。