基于飽和土壤埋深調控的水稻節水灌溉技術研究

徐俊增 程 衡 衛 琦 陳 鵬 欒雅珺 蔡少杰

(1.河海大學農業科學與工程學院， 南京 210098； 2.河海大學水文水資源與水利工程科學國家重點實驗室， 南京 210098)

0 引言

隨著水資源的日益緊缺，提高農業用水效率已成為保障糧食安全和水安全的重要措施[1-5]。水稻作為我國主要糧食作物，其耗水量約占農業用水量的70%、全國總用水量的50%[6]。在此背景下，“淺、濕、曬”灌溉[7-8]、水稻強化栽培[9]、控制灌溉[10]、間歇灌溉[11]等節水灌溉技術已被大規模應用。盡管不同節水灌溉制度對水稻增產作用還存在不確定性，但在提高水分利用效率方面已被廣泛認可[12]。

為掌握水稻水分虧缺狀況、及時進行灌溉管理，需要確定合理的灌溉調控指標。現行的各種水稻節水灌溉技術在調控指標與觸發灌溉的指標閾值方面略有不同。對于傳統淹水灌溉來說，田間水層是稻田灌溉的首要控制指標。淺濕灌溉秉承淺水勤灌的理念，一般以30 mm為上限、5 mm為下限，其灌水量有所降低，但灌水頻率增加。通常情況下在一次足量灌溉后維持田面3～5 d內有水層，當水全部下滲進入土壤后再保持田面無水層3～5 d，之后復水，使稻田呈現周期性的干濕狀態，稱之為干濕交替灌溉[13]。田間試驗發現，在生育期內控制稻田呈現周期性無水層變化的水稻長勢較好。土壤水勢被用來作為水稻節水灌溉的調控指標，相關研究表明，水稻節水灌溉的水勢閾值范圍一般為-40～-20 kPa，且在不同生育階段其閾值有所差異[14]。與土壤水勢相似，土壤體積含水率也作為水稻節水灌溉控制指標(多為相對飽和含水率，在0.60～0.85 cm3/cm3之間)，并被廣泛應用，但二者都具有空間變異性大等缺點，因此在大面積推廣應用時需要大量的傳感器來滿足對土壤水分狀況的監測。為了解決監測精度低、測量成本高等問題，在節水灌溉技術推廣過程中，也有采用足跡深度、稻田裂縫程度等對設備依賴性較小的土壤描述性指標，以觸發節水灌溉[15]。但足跡深度、裂縫程度、無水層天數主要依靠農民的生產經驗，其精確性尚不明確，甚至無法合理度量，因此在指導水稻節水灌溉方面存在明顯缺陷。

上述提到的大部分水稻節水灌溉技術，在灌溉后田面大多處于淹水或飽和狀態，隨著水分的消耗淹水層逐漸消失，一定厚度的土壤開始呈現非飽和狀態，且隨著落干脫水過程而逐漸變厚。這就意味著在飽和與非飽和土層之間存在一個向下移動的淺層水位，其對應深度定義為飽和土壤埋深。假設不同生育期根區飽和土壤埋深存在一個臨界點，該點能否成為觸發節水灌溉的替代指標值得進一步探討。因此，本文結合在黑龍江省大面積推廣應用的水稻控制灌溉技術[16]，采用盆栽試驗與模型(Hydrus-1d)模擬相結合的方法，研究稻田無水層階段飽和土壤埋深與土壤體積含水率的變化規律，以確定水稻不同生育階段的飽和土壤埋深臨界值。

1 材料與方法

本試驗于2017年5—11月在黑龍江省慶安灌溉試驗站進行，該地區屬于寒溫帶大陸性季風氣候，多年平均氣溫2.5℃，多年平均降水量550 mm，降雨多集中在7—9月。試驗區土壤類型為黑土，有機質質量比41.5 g/kg，堿解氮質量比154.7 mg/kg,有效磷質量比32.3 mg/kg，速效鉀質量比122.9 mg/kg。盆栽試驗在直徑50 cm、高度70 cm柱形桶中進行，將風干、破碎、過篩(4 mm)預處理后的土壤裝入桶內，土壤基本物理性質如表1所示。在每個桶底部土壤下面布設厚度為5 cm的細砂過濾層，過濾層內部埋設透水管道，透水管道通過筒壁連接一個控制閥門，通過調節閥門開度收集排水，模擬深層滲漏。

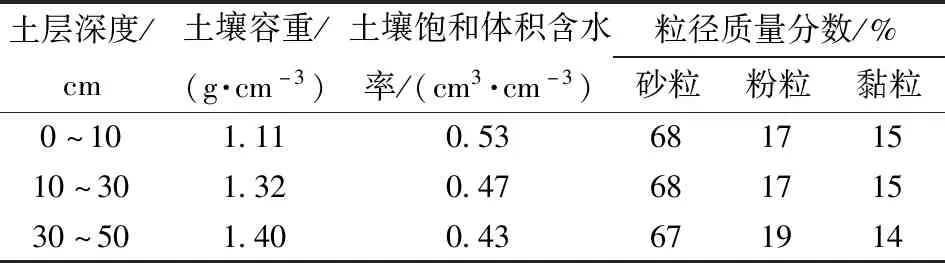
表1 土壤基本物理性質Tab.1 Soil basic physical properties

水稻采用控制灌溉模式進行灌溉管理，不同生育期土壤灌水下限如表2所示。根據試驗區深層滲漏情況設置3種滲漏強度(1、2、3 mm/d; 記為D1、D2、D3)。滲漏水由與細砂過濾層相連的控制閥門按設定體積每小時排出1次，D1、D2、D3處理對應的排水量分別為8.2、16.4、24.5 mL/h。水稻品種為龍慶3號，于2017年5月20日以4株/盆的密度移栽至盆栽，9月27日收獲；根據當地栽培習慣，全生育期的氮肥(N)、磷肥(P2O5)、鉀肥(K2O)的施用量分別為110、45、80 kg/hm2。

表2 不同時期水稻根系深度、根區及土壤水分下限Tab.2 Root depth, root zone and soil water lower limit of rice in different periods

每個盆栽分別在5、15、25、35 cm深度埋設HOBO EC-5型土壤水分傳感器測量土壤含水率，并使用HOBO H21-002型數據記錄儀記錄每小時的土壤含水率。背離排水口一側預埋直徑為50 mm的PVC管，管身鉆孔并用土工布包裹防止泥沙進入，管內放置Dataflow型電容式水位記錄儀，用于測量飽和土壤埋深，監測頻率為每小時1次。每次灌水至土壤飽和并在田面保留約3 cm水層，灌水量采用量程為100 mL、精度為1 mL的玻璃量筒記錄。降雨量由氣象站測定。當降雨后桶內水層高度超過3 cm時，記錄初始水層高度，并排水至土表水層為3 cm。土壤水分蒸發采用蒸發皿(直徑113 cm、高度150 cm)進行觀測，監測頻率為每2 h 1次，蒸散發量通過水量平衡方程計算[17]。

2 Hydrus-1d模型構建

2.1 Hydrus-1d模型

Hydrus-1d是根據Richard方程數值解建立的適用于飽和區和非飽和區的土壤水分運移模擬模型[18]，采用正交試驗法，可模擬水稻根區土壤水分的動態變化過程，公式為

(1)

式中θ——土壤體積含水率，cm3/cm3

K——滲透系數，cm/d

ψ——基質勢頭，cm

S——根系吸水速率，cm3/(cm3·d)

z——土層深度，cm

t——時間，d

稻田土壤的水力特性用Van Genuchten的K-θ和ψ-θ關系進行描述，即

(2)

(3)

其中

m=1-1/n

(4)

式中θr——殘余體積含水率，cm3/cm3

Ks——飽和導水率，cm/h

α——經驗擬合參數，cm-1

n——孔徑指數

l——孔隙連通性參數，取0.5

同時根據Feddes模型計算根系吸水速率，即

S(z,t)=α′(ψ,z)b(z)Tp

(5)

其中

(6)

式中α′(ψ,z)——水分脅迫響應函數

b(z)——根系分布函數

Tp——作物潛在蒸騰速率，cm/d

d——根系層深度，cm

將水稻潛在蒸散發劃分為潛在植物蒸騰和土壤蒸發量，即

Tp=ETp(1-e-kLAI)

(7)

Ep=ETpe-kLAI=ETp-Tp

(8)

式中ETp——潛在蒸散發量，cm/d

Ep——作物潛在蒸發速率，cm/d

LAI——葉面積指數

k——冠層消光系數，水稻一般取0.3

2.2 邊界與初始條件

假設模擬區域為一維剖面，將40 cm土層深度有限差分為41個節點網格，所有節點間距均為1 cm。土壤剖面按深度分為0～10 cm、10～30 cm和30～40 cm共3層。地表邊界(上邊界)采用表面可產流的大氣邊界，邊界條件為能反映大氣、水、土壤和植物相互作用的時間變量；水分從土壤表面蒸發的速率等于潛在蒸發速率，假定基質勢的臨界值比土壤表面的基質勢低，此處取-10 000 cm；底部邊界為變通量邊界，流量為深層滲漏量；側邊界為不透水邊界。土壤初始水分狀況設置為飽和含水率并用壓力水頭進行表征。

2.3 模型率定與驗證

基于表1土壤容重和粒徑質量分數測定結果以及Hydrus-1d自帶神經網絡預測模塊預測得到的0～10 cm、10～30 cm、30～40 cm土層土壤水動力參數初選值，利用D1和D3的實測數據對Hydrus-1d模型進行率定，并通過在模型中輸入每小時的潛在蒸發、蒸騰、基質勢頭、降水、灌溉和土壤水力參數等數據，反演得到Hydrus-1d模型中的α、n和k參數值。在此基礎上，根據D2的實測數據對率定模型的準確性進行驗證。

2.4 模擬情景設置

由于實際應用中不同灌區陽光照射時長、降雨量、溫度、下墊面等環境因素存在差異，因此，其相應的土壤滲漏及作物蒸發蒸騰量也有所不同。為進一步分析不同耗水強度導致的飽和土壤埋深指標差異，借助率定的Hydrus-1d模型對不同滲漏強度和蒸發蒸騰強度組合進行了情景模擬。其中蒸發蒸騰強度的選擇參考了相關研究結果[19-21]以及本研究的試驗結果，滲漏強度根據當地土壤類型及地區經驗進行確定。如表3所示，在每個生育階段，按照蒸發蒸騰強度和滲漏強度不同組合均設置了 9 種模擬情景，每種組合的小時蒸發蒸騰量根據日蒸發蒸騰量乘以加權系數進行劃分，其中06:00—18:00的加權系數為0.067，其余時段的值均為0.016。由于僅針對一次落干脫水過程開展模擬，因此不考慮降雨的影響。基于模擬的土壤水分與飽和土壤埋深動態變化，分析不同耗水強度下兩者之間的定量關系，對照水稻控制灌溉土壤水分控制指標，計算對應的飽和土壤埋深臨界值，研判耗水強度差異對飽和土壤埋深控制指標的影響。

表3 水稻各生育期稻田蒸發蒸騰強度及滲漏強度控制指標

3 結果與討論

3.1 土壤含水率和飽和土壤埋深同步變化規律

盆栽試驗結果如圖1、2所示，各處理土壤含水率在灌水后均隨時間的延續而減少，且在不考慮處理間水稻騰發量差異的情況下，耗水量均隨深層滲漏強度的增加而增加，其相應的土壤含水率下降幅度也依次增大。時間變化方面，當作物蒸騰作用較強時，土壤含水率下降較快，且飽和土壤埋深隨土壤含水率的降低而增加(圖2)。不同處理飽和土壤埋深呈現與土壤含水率變化相似的規律，即隨著灌溉后時間的推移，飽和土壤埋深隨土壤含水率的降低而增加(水位下降)。由此推斷，可以考慮將飽和土壤埋深作為土壤含水率的替代指標，用于觸發水稻節水灌溉。

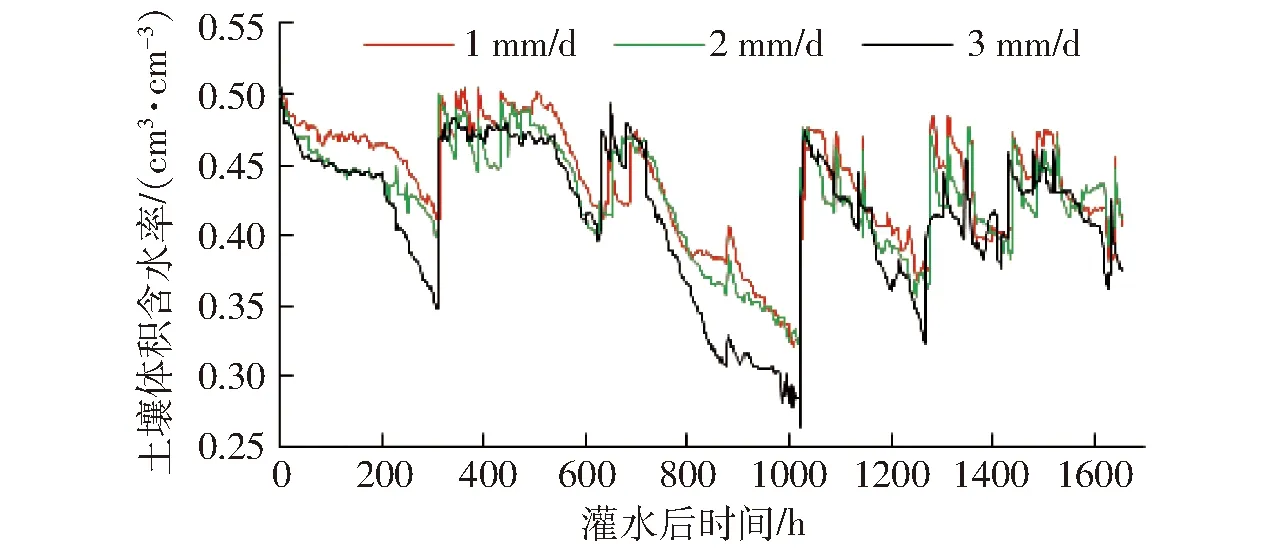
圖1 節水灌溉稻田土壤體積含水率變化趨勢Fig.1 Trend of soil moisture content in water-saving irrigation paddy field

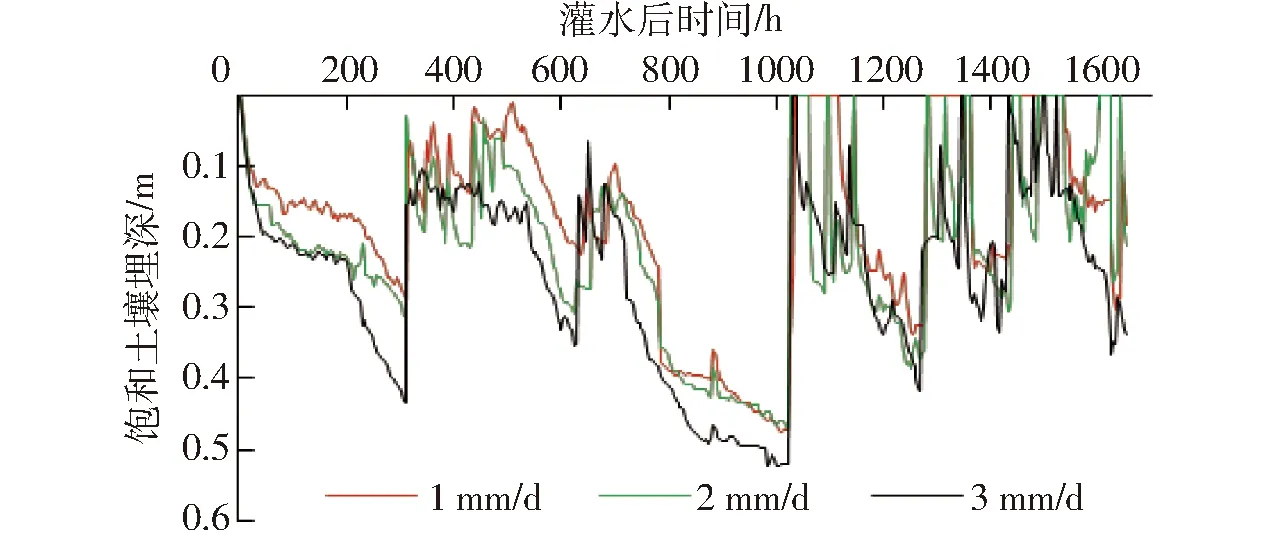
圖2 節水灌溉稻田飽和土壤埋深變化趨勢Fig.2 Trend of depth of saturated soil in water-saving irrigation paddy field

水稻根系層土壤含水率與飽和土壤埋深之間存在較好同步關系。通常情況下，滲漏強度越大，飽和土壤埋深增加的速率越大，而土壤體積含水率與飽和土壤埋深隨時間的變化趨勢則呈負相關關系，由統計可知兩者同步變化規律均符合二次拋物線關系，具體見表4，決定系數R2基本達到0.96以上。因此，基于二者之間的定量關系，將黑龍江省水稻控制灌溉常用的土壤含水率灌水下限換算成對應的飽和土壤埋深，如表5所示。結果發現水稻不同生育階段的飽和土壤埋深臨界值主要維持在0.31～0.50 m范圍內，其中分蘗后期飽和土壤埋深臨界值最大，其對應的節水灌溉土壤水分控制下限也最低。

表4 水稻不同生育期土壤含水率與飽和土壤埋深的關系Tab.4 Relations between soil moisture content and depth of saturated soil in different growth stages of rice

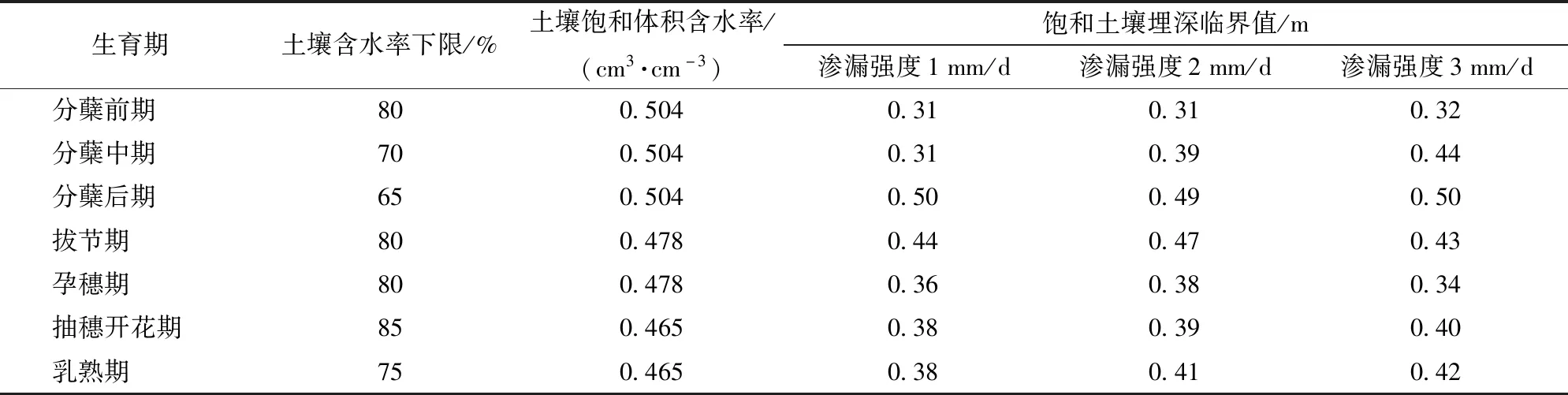
表5 不同耗水強度下水稻不同生育階段飽和土壤埋深控制指標Tab.5 Control index of depth of saturated soil in different growth stages of rice under different water consumption intensities

3.2 模型率定與應用

3.2.1模型率定與驗證

利用2017年D1和D3處理(滲漏強度為1 mm/d 和3 mm/d)數據對Hydrus-1d模型進行率定，相關參數見表6。且圖3結果表明，D1和D3模擬的土壤含水率與實測土壤含水率具有較好的相關性，相關系數分別為0.806和0.831，均方根誤差分別為0.019 cm3/cm3和0.023 cm3/cm3。此外，基于D2(滲漏強度為2 mm/d)數據對率定模型的準確性進行驗證，結果(圖4)表明率定模型模擬的土壤體積含水率與實測的土壤體積含水率變化趨勢較為吻合，其相應的相關系數和均方根誤差分別為0.758和0.021 cm3/cm3。據此，率定后的Hydrus-1d模型能夠較好地模擬節水灌溉稻田落干脫水過程中土壤水分動態，可以作為模擬更多耗水強度情境下稻田水分落干脫水過程中土壤水分變化的工具。

表6 率定后的Hydrus-1d水力參數Tab.6 Calibrated hydraulic parameters of Hydrus-1d model

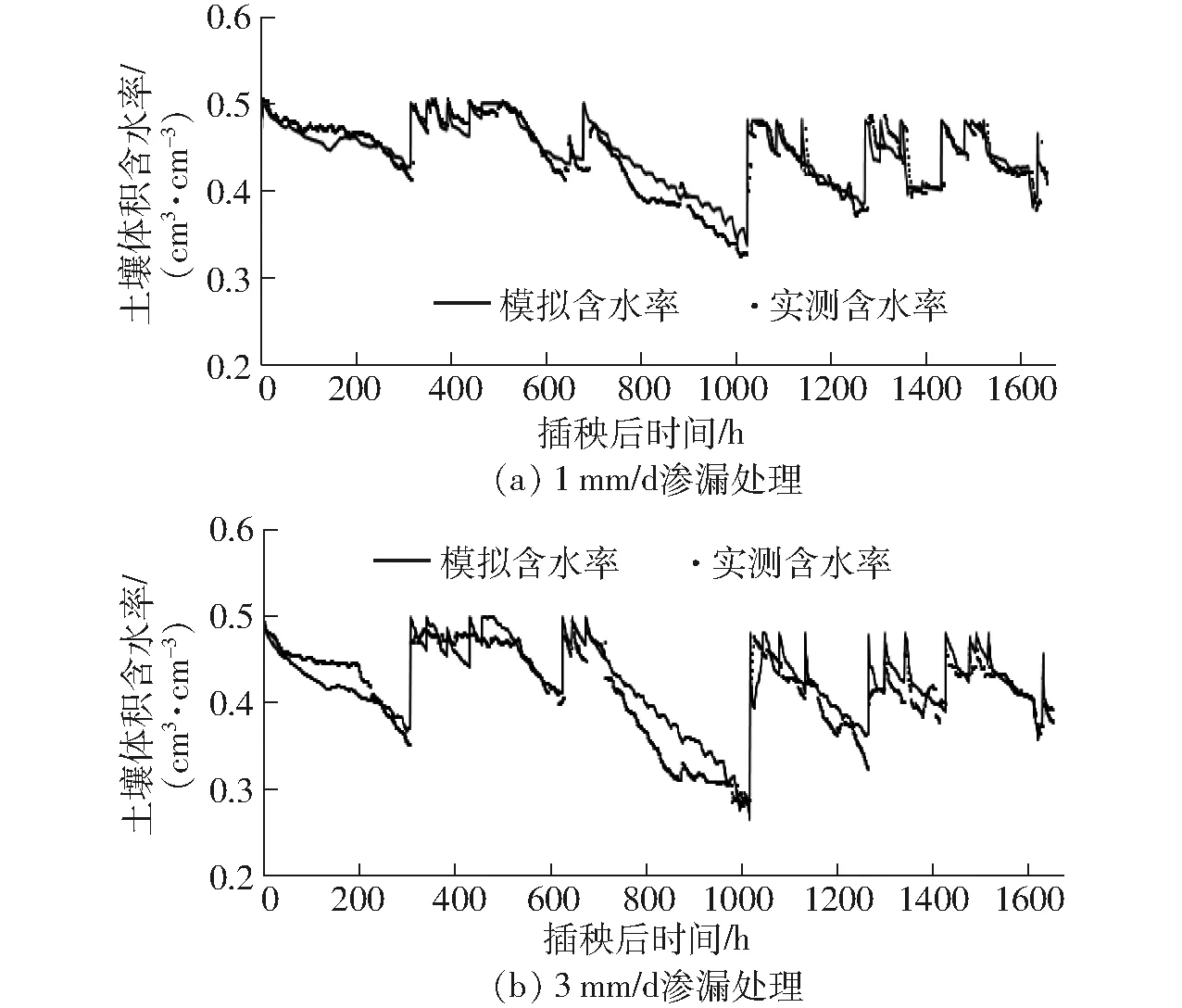
圖3 土壤水分運動模型率定Fig.3 Calibration of soil water movement model

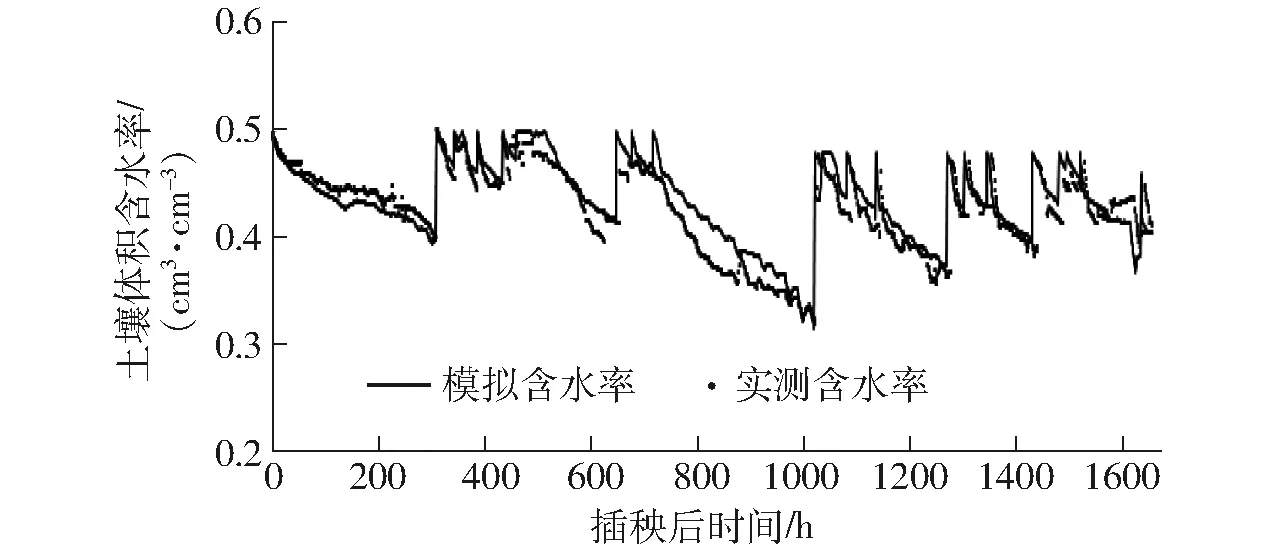
圖4 土壤水分運動模型驗證Fig.4 Validation of soil water movement model

3.2.2基于Hydrus-1d的情景模擬分析

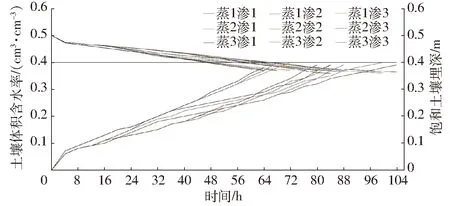
圖5 水稻分蘗前期不同耗水組合下土壤體積含水率與飽和土壤埋深變化過程Fig.5 Variation of soil water content and depth of saturated soil under different water consumption combinations in early tillering stage of rice

借助率定模型對稻田不同蒸發蒸騰強度與滲漏強度組合下稻田落干脫水過程進行情景模擬，得到了水稻各生育期9組水分與水位同步變化的曲線。以分蘗前期為例展開分析，由圖5可以看出，其土壤體積含水率指標的灌水下限為0.4 cm3/cm3。不同耗水處理下土壤水分運動規律較為相似，即隨著耗水過程中土壤含水率的降低，飽和土壤埋深逐漸增加；且耗水強度越大，土壤含水率下降越快、飽和土壤埋深增加越快，到達灌水下限所需的時間越短。此外，基于多種情景模擬下土壤含水率與飽和土壤埋深的結果，定量分析了水分下降過程中土壤體積含水率與飽和土壤埋深的關系，結果表明二者之間呈二次拋物線關系。

基于情景模擬的結果，統計得到了各生育期不同耗水強度下稻田落干脫水到達灌水下限的消退時間及飽和土壤埋深臨界值。以分蘗前期和拔節期為例，結合圖6和表7可以看出，不同耗水強度條件下飽和土壤埋深臨界值變化范圍均相對較小，其區間分別為(0.27 m，0.28 m)和(0.51 m，0.57 m)。但消退時間之間存在明顯差異，兩個生育階段不同耗水情景下稻田落干脫水到達灌水下限的消退時間之間最大差異分別為20 h和29 h。以往基于無水層天數的研究大多針對固定的無水層持續時間，未考慮土壤滲漏條件、不同生育期作物需水量等因素差異的影響，進而導致不同耗水強度下稻田經落干脫水到達灌水下限的消退時間的差異未有呈現，科學性略顯不足。相比之下，飽和土壤埋深指標指導水稻節水灌溉在不同耗水強度條件下差異相對較小，較為穩定，因此，可以認為是一個相對通用且合理的控制指標。

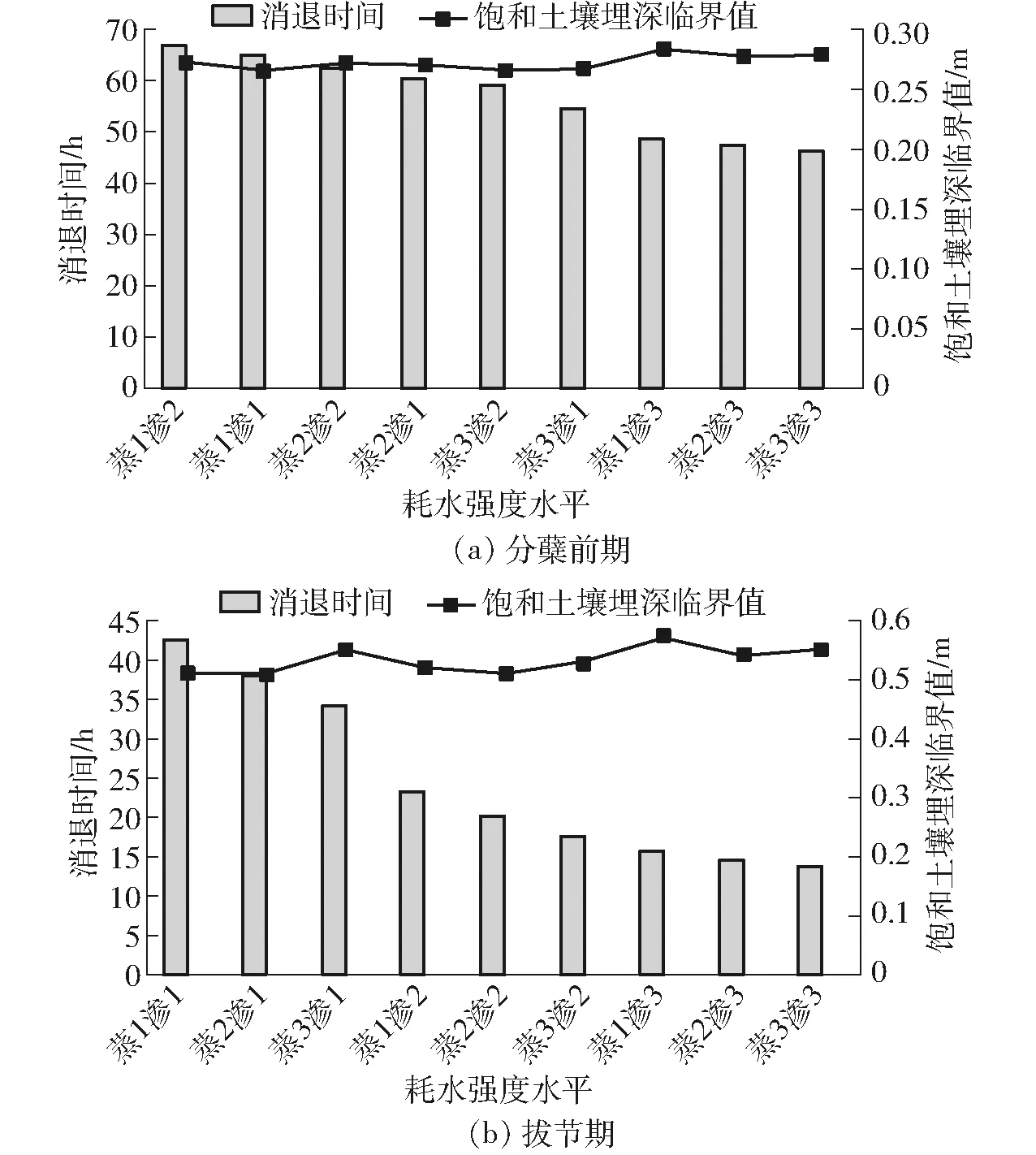
圖6 不同耗水強度下稻田到達灌水下限的消退時間及飽和土壤埋深臨界值Fig.6 Time to reach lower limit of irrigation and critical value of depth of saturated soil under different water consumption intensities

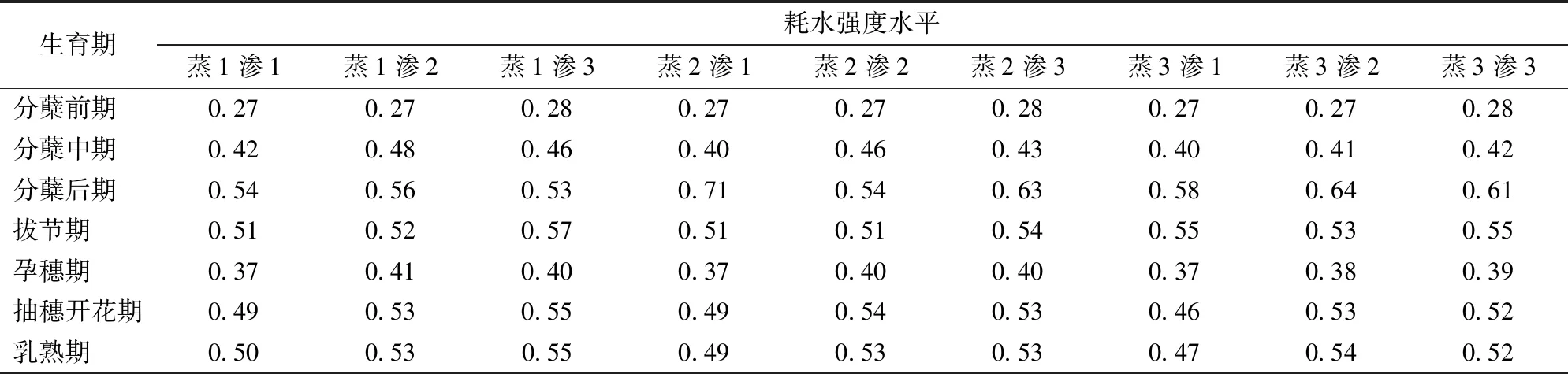
表7 不同耗水強度組合下水稻不同生育期飽和土壤埋深臨界值Tab.7 Critical value of depth of saturated soil at different growth stages of rice under different water consumption intensity combinations m

3.2.3水稻節水灌溉飽和土壤埋深指標

綜合盆栽試驗結果和模型模擬結果，在考慮水稻種植區氣候、土壤特性等因素的基礎上，選取了高、中、低(3、2、1 mm/d)3種滲漏強度，并以不同耗水強度下各生育期試驗或模型模擬給定的臨界值中的最小值(偏于安全)為控制灌溉最適宜標準，擬定了黑龍江省水稻節水灌溉飽和土壤埋深臨界值,如表8所示。結果表明，水稻在分蘗前期(根系較淺)的飽和土壤埋深控制指標較小，為0.27 m，分蘗后期土壤水分控制下限最低，其相應的飽和土壤埋深控制指標也最大，為0.50 m。對比不同滲漏強度下的結果可以發現，飽和土壤埋深臨界值除了在分蘗中期極差達到0.09 m外，在大部分生育階段的極差均維持在0.04 m以內。

3.3 討論

田間試驗和經驗總結是確定水稻節水灌溉控制指標的兩種主要方法，其中土壤含水率和田間無水層天數等為控制指標的水稻節水灌溉技術已經得到了較大面積的推廣應用，但其在投入成本、空間變異性、數據可靠性等方面存在的缺點仍限制了其更廣泛的應用。而本研究提出的以飽和土壤埋深為控制指標的灌溉技術，僅需布置一個水位觀測井和一個水位計即可實現對一定范圍內不同地下水位的連續測量，克服了傳統以土壤含水率為控制指標的節水灌溉技術需要在不同土壤深度埋設多個土壤水分傳感器所帶來的一系列問題[22-23]。且調研結果表明，同等價位下水位計的測量精度遠高于土壤水分傳感器，因此，在投入成本相近的條件下以飽和土壤埋深為控制指標的灌溉技術具有監測成本低、監測精度高等優勢。

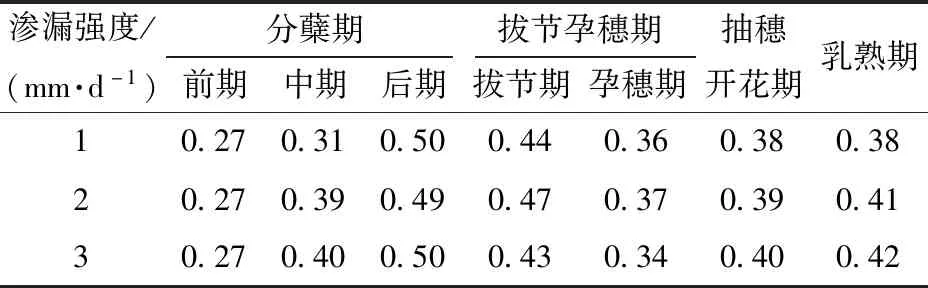
表8 不同耗水強度下水稻控制灌溉飽和土壤埋深臨界值Tab.8 Critical value of depth of rice saturated soil under controlled irrigation with different water consumption intensities m

此外，文獻[24]研究節水灌溉稻田的節水增產機理時發現，當田間無水層持續3～4 d后，盆栽中有明顯裂痕，大田裂痕逐漸顯現。文獻[25]通過研究控制灌溉技術與生產用水的關系，提出了以目測稻田裂縫寬度表述土壤水分狀況，并給定了不同裂縫寬度對應田面土壤含水率參考值。而本研究結果表明，以飽和土壤埋深為控制指標的灌溉技術主要在田間落干后3～5 d進行灌溉，且能夠以具體的灌水下限臨界值對稻田水分虧缺狀況作出反饋，相比于無水層天數和裂縫寬度等經驗性指標更加精準、合理。

本研究通過開展盆栽試驗，并結合Hydrus-1d模型模擬的方式實現了對不同田間蒸發蒸騰量與滲漏量組合情景的考慮，獲得了相對可靠的結果，可以在不同的耗水情境下予以應用和驗證。但本研究局限于盆栽試驗，且僅針對垂直方向上的水分運移進行了模擬；而在田間尺度上還存在水平方向上的水分運移、以及靠近排水溝一側大田側向排水等情況，這些均可能導致飽和土壤埋深的差異。

4 結論

(1)以不同滲漏強度(1、2、3 mm/d)處理下的土壤含水率實測值為依據，對Hydrus-1d模型進行了率定及驗證，構建了適用于飽和土壤埋深調控指標的Hydrus-1d模型，驗證結果表明，該模型能夠較好地模擬稻田落干脫水過程中飽和土壤埋深和土壤含水率的同步變化規律。

(2)試驗和模擬結果均表明，節水灌溉稻田土壤含水率與飽和土壤埋深之間呈現較好的二次拋物線關系，基于此將試驗區傳統的土壤含水率指標臨界值轉換為對應的飽和土壤埋深指標臨界值，得到水稻各生育期臨界值區間為(0.27 m, 0.50 m)，由此提出了基于飽和土壤埋深調控的水稻節水灌溉技術。

(3)該技術采用易于觀測的飽和土壤埋深作為控制指標，具有監測精度高、成本低、空間連續性好等特點，比傳統節水灌溉的控制指標更加科學合理，在準確反映田間水分狀況的同時，能夠滿足節水灌溉規模化應用的需求。