基于優化ADRC的單臂機器人軌跡跟蹤研究

陳 壯，王憲倫，陳 閃

(1.芯恩(青島)集成電路有限公司，山東 青島 266000;2.青島科技大學機電工程學院，山東 青島 266061;3.青島濱海學院機電工程學院，山東 青島 266555)

0 引言

機器人抓取物體的工作看似簡單，實際上是多耦合的非線性軌跡解算過程[1]。對于機器人末端執行器的軌跡規劃，一般將末端執行器的笛卡爾坐標系由運動學算法映射到關節空間中，解算并擬合得到理想的抓取角位移軌跡和角加速度，將關節變量轉換成脈沖值發送給伺服電機完成各軸的協同動作。但是實際上機器人常處于微振動的環境中，不可避免地受到自身共振和地面振動的不確定撓動，導致抓取軌跡與擬合的軌跡偏離。為了使機器人高精度跟蹤抓取軌跡，需要在已知機器人的運動學和動力學模型的前提下構造軌跡跟蹤控制系統。

Yu等[2]為了減輕內外部的干擾耦合對無人直升機螺旋槳操控的影響，建立了ADRC自抗撓模型，對比PID控制算法，提高了系統的動態穩定性。Wang等[3]將自抗撓模型應用于交流電，估計逆變器的周期性負載擾動。廖薇等[4]構造了ADRC模型使得海洋絞車適用于不同線纜直徑和重量的工況，即使當環境變化時，控制器也能保持良好的動態性能，對比了PID控制器，證明了ADRC有較快的響應速度和抗干擾能力。

自抗擾控制(ADRC)算法是在PID控制理論基礎上延伸發展而來的[5]，能自主抵抗機器人內外部的各類干擾，具備高精度的軌跡跟蹤能力，并且其關鍵參數也可以根據實際跟蹤能力進一步優化。

1 關節空間動力學模型

實驗用的是加拿大Kinova公司研發的MICO2仿人六軸串聯機器人，在關節空間下對應位置和時間的拉格朗日動力學方程的一般形式為

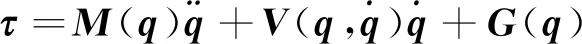
(1)

(2)

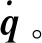
(3)

2 建立ADRC模型

標準二階ADRC由微分跟蹤器(TD)、非線性狀態誤差反饋(NLSEF)和擴張狀態觀測器(ESO)獨立的3部分組成，如圖1所示。變量q為機器人各關節軸輸出的角位移，設定變量qc為機器人關節擬合軌跡的任意位置，變量qc1為輸入軌跡qc的跟蹤信號，qc2為輸入軌跡qc微分后速度的跟蹤信號，它們由ESO實時提取跟蹤值qc1和qc2，從而確保跟蹤值的穩定性。κ為系統內外的不確定干擾；τ為考慮內外干擾引入的系統補償量。

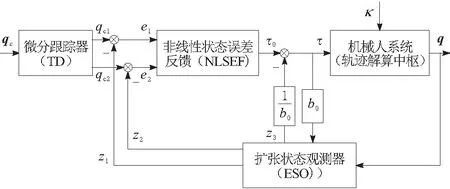
圖1 二階ADRC框架模型

跟蹤值qc1和qc2的二階非線性跟蹤微分器TD函數形式為

(4)

k=fh(qc1-q，qc2,r0,μ),r為跟蹤速度控制因子，一般|k|≤r；r0為r的整數倍，一般按實際控制需求選擇合適的倍數；h為軌跡采樣周期，μ為噪聲濾波控制因子，一般為h的20倍；fh為控制反饋跟蹤函數。

ESO是自抗擾控制器的核心，用于跟蹤變量，估計并補償不確定撓動以消除系統噪聲，這也是PID沒有的功能。設變量z1為qc1的估計值，變量z2為qc2的估計值，變量z3為擴張變態變量。β1、β2、β3為ESO內部參數，構建ESO算法為

(5)

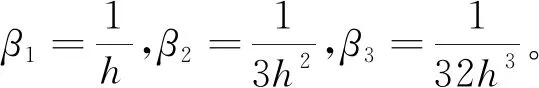
至此，已經通過ESO估計了機器人內外不確定撓動，為了使撓動的抵消變得可控，引入非線性狀態誤差反饋(NLSEF)。NLSEF是自抗擾控制器特有的組成部分，流程如圖2所示，用于調整增益限制系統撓動，調節速度在較小的范圍內波動從而避免超調。已知TD跟蹤得到的角位移qc1和速度qc2，以及ESO得到軌跡估計值z1和速度估計值z2。對應數值做差法運算得到跟蹤誤差e1和e2。結合控制反饋跟蹤函數fh，得到NLSEF表達式為

(6)

c為阻尼系數。

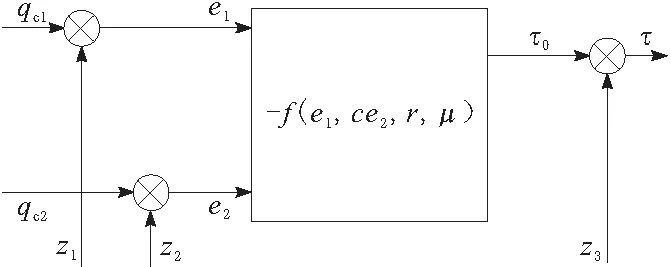
圖2 NLSEF計算流程

3 軌跡跟蹤仿真

外部干擾對軌跡的影響，主要體現在末端執行器角位移變量的瞬時幅值存在噪聲且角加速度響應延遲[6-7]。選擇Kinova MICO2的第3關節軸跟蹤已規劃的關節角位移變量q為例，驗證二階ADRC設計的可行性。ADRC跟蹤結果如圖3所示。由圖3可知，當存在干擾時，第3關節軸反饋的實際關節角位移受噪聲干擾的影響較明顯，明顯偏離理想的規劃軌跡，而經過ADRC估計并補償擾動后使得跟蹤控制的角位移能夠近似向規劃的軌跡趨近。

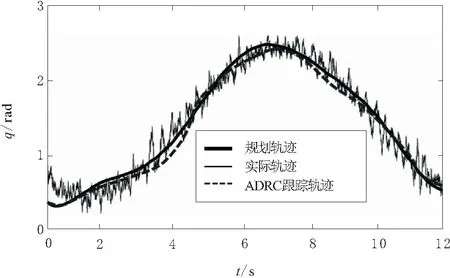
圖3 第3關節關節角位移軌跡

4 ADRC參數優化

ADRC算法在運算效率和跟蹤干擾等方面都優于PID算法，甚至不依賴于數學模型。各部分參數的優化起著至關重要的作用。考慮到閉環系統的動態特性，為了避免因數據量較大而造成誤差信號時滯現象，需要根據誤差補償值動態微調ESO的內部參數β1、β2、β3以及NLSEF的參數kp。參數kp的選取影響著目標值跟蹤精度，過大會出現超調現象，因此需要從非線性控制率層面抑制系統超調，減小振蕩。

進一步解算kp的最優解，設計了一種基于遺傳算法優化徑向基網絡算法(GA-RBF)實時優化ADRC。RBF神經網絡能精準快速逼近設定值，同時由遺傳算法(GA)的強魯棒性并行搜索優化徑向基函數(RBF)的網絡權值并避免局部極小值，盡可能完善RBF神經網絡[8-9]。RBF高斯逼近激活函數為

(7)

隱含層激活函數φ(‖x-ui‖)一般為

φ(‖x-ui‖)=exp(-‖x-ui‖2/σ2)

(8)

‖x-ui‖為基函數與輸入矩陣的差向量；g矩陣為權值；σ為函數寬度閾值參數，影響RBF徑向范圍；p為神經元數量；ui為第i個節點的聚類中心。

通常采用GA并行全局搜索RBF的最優解。GA優化RBF網絡的權值流程如圖4所示。設定二進制編碼，迭代種群規模為N，借鑒生物繁殖理念，選擇過程則以評價染色體的方式擇優交叉組合產生新的后代，交叉概率和變異概率則跟隨適應度改變。當滿足迭代閾值時，停止迭代并輸出此時種群中最大適應度的個體作為最優權值。網絡權值預測數值變化情況如圖5所示。

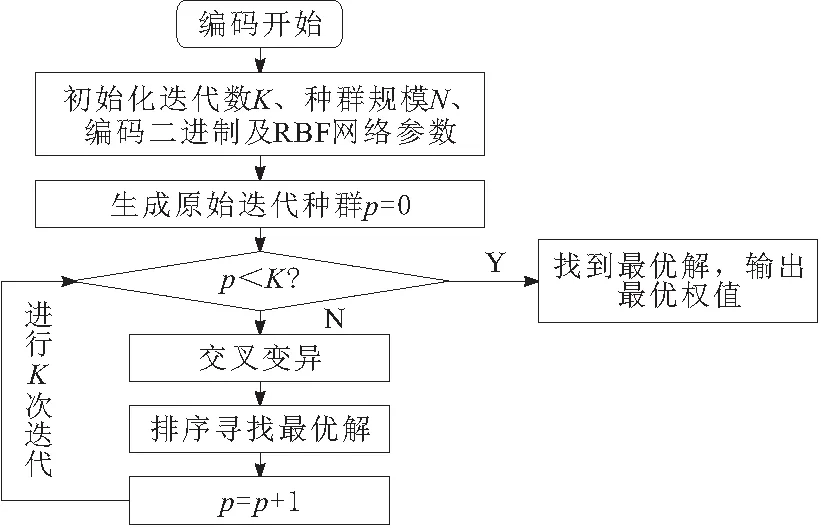
圖4 GA優化RBF網絡的權值流程

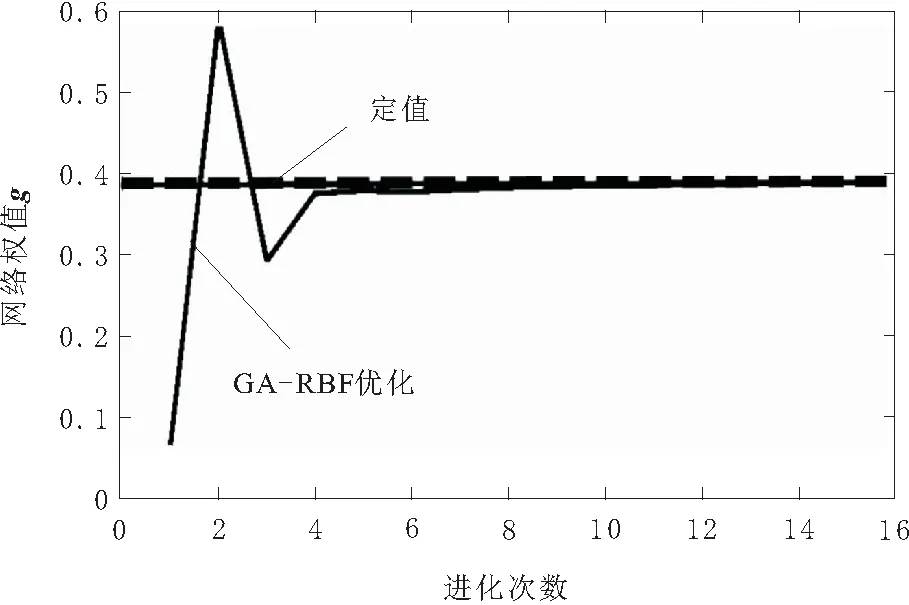
圖5 網絡權值預測數值變化

由圖5可知，在迭代初期，RBF的網絡權值g有較大的波動，使得預測值不可靠，隨著迭代進化次數的增加使得權值預測值逐步趨于穩定。這也意味著GA預測的最小誤差也跟隨迭代進化次數的增加逐步收斂至0。使得在當前ADRC跟蹤模型下，預測了合適的RBF網絡權值g，通過RBF網絡優化了NLSEF，微調參數kp，最終實現更高的逼近精度。

5 實驗誤差分析

第3關節角位移變量q由GA-RBF優化后的ADRC跟蹤結果與規劃軌跡作差，得到絕對誤差偏移量δ，如圖6所示。通過偏移幅值清楚地看出該關節的各離散點的跟蹤誤差臨界波動較小，角位移絕對誤差偏移量δ基本上能控制在-0.25～0.25 rad范圍內，且誤差可控。從而將算法映射到機器人的6個關節軸，各軸協同工作使得機器人末端執行器實時跟隨已規劃的軌跡工作。

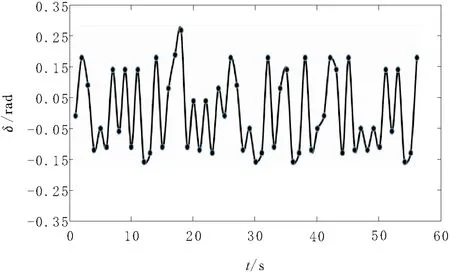
圖6 ADRC跟蹤誤差

6 結束語

機器人普遍存在來自內外界的不確定性干擾，為了使得機器人更好地遵循規劃好的軌跡運行。本文以Kinova MICO2為例，在關節空間下建立了ADRC關節角位移跟蹤模型。為了確保ADRC適用于各類復雜環境，保證其閉環誤差跟蹤穩定性。建立GA-RBF網絡進一步優化了NLSEF參數kp，控制角位移跟蹤誤差在一定時間內穩定在可接受的范圍內，表明GA-RBF優化的ADRC使機器人實際工作軌跡向著規劃軌跡收斂。