基于理解性學習的生態課堂

戴榮

[摘? 要] 生態課堂作為一種理念，得以實現依賴于理解性學習為內涵的學習過程，這樣的課堂可以發展學生的核心素養. 文章以“數列的概念及其表示”為例，結合教學實踐探索了情境引領是前提、體驗中學習是根本的理解性學習的生態課堂.

[關鍵詞] 理解性學習;生態課堂;情境;體驗

數學課堂教學需以生為本，那么在教學的過程中，理解無疑是排在首位的. 當下，“數學理解”已然成為一線數學教育工作者和數學教育家們密切關注的話題. 所謂的理解性學習，就是指學習者在充分理解的基礎上進行學習. 由此可見，學習是以“理解數學”為目標指向的，同時隨著學習的推進促成對數學的深刻理解. 理解性學習關注發展，強調師生以及外在環境間的一種有機整合，重視數學理解. 如果說生態課堂是一種理念，那么生態課堂得以實現源自理解性學習為內涵的學習過程，這樣的課堂可以發展學生的核心素養[1]. 那么，怎樣構建這樣的理解性學習的生態課堂呢？下面，筆者以“數列的概念及其表示”的教學為例，談談如何開展理解性學習，營造生態課堂，在課堂教學中發展學生的數學核心素養，以達“立德樹人”的目標.

教學案例

1. 理解性情境導入

戰國時期著名的哲學家莊周曾在所著的《莊子·天下篇》說道：“一尺之棰，日取其半，萬世不竭.”我們可以將這句話中的“一尺之棰”每日剩余部分以數據按照順序排成一列：1，■，■，■，….

設計意圖：學生的學習興趣源于好奇心，執教者以歷史名言為切入點引入課堂，弘揚數學文化的同時勾畫了數學與生活的關聯，激發了學生一探究竟的欲望. 同時，以數代語，讓學生從字句間的領悟中實現從現象到本質的理解，使教學達到了事半功倍的效果.

啟示：本課雖然是借班上課，但執教者在課堂引入部分睿智地引用了與課題相契合的名言，充分吸引了學生的注意力. 在這樣的生態課堂中，學生盡情張開想象的翅膀，感受著教師的情感，綻放出理解性思維的光芒.

2. 理解性活動設計

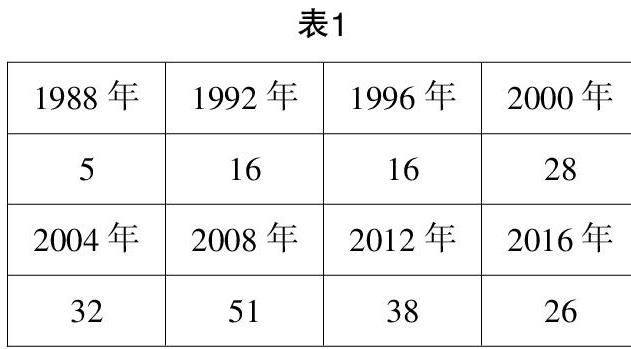
活動1：表1為1988年至2016年中國在各屆夏季奧運會所獲得的金牌數：

請將1988年至2016年中國在各屆夏季奧運會中獲得的金牌數排出一列數.

活動2：以小組為單位，試著將一個邊長為1的正方形紙片對折n（n∈N*）次，并在表2中記錄每一次對折中紙的層數的變化情形以及面積變化情形.

設計意圖：數學概念從來都不是從天而降的，它的形成是依賴已有數學概念基礎，以及多種方式和不同側面的理解才能加以定義. 執教者設計以上兩個活動，引導學生觀察、分析和操作，直觀感知數列的“生活味”，并通過實踐操作，實現學生對數列本質的理解. 因此，學生在直觀感知和操作實踐的過程中，可以逐步完成對數列本質的理解性掌握.

啟示：教師設計活動的根本目的在于引導學生通過活動感知概念本質. 在活動的過程中，教師可以掌握學生理解的進程，獲得學生理解的深度，隨時跟蹤學生的獨特性理解，明晰存在的問題，等等;學生可以通過活動生成對數列概念多角度、多層次的理解和認識，深化自身的認知結構，這也是理解性學習的本質所在.

3. 理解性探究

問題探究一：以上所給出的例子中，都可以得出一列數，經過觀察，你們發現它們有何共同點？

生1：它們都是一列數.

生2：它們均有一定的次序.

師：總結得很到位！誰能結合以上羅列的共同點用自己的話說一說什么是數列嗎？

生3：按一定次序排列的一列數，就是數列.

問題探究二：（1）38，51，2，28，16， 16，5，15是數列嗎？

（2）集合{1，2，3}與集合{3，2，1}相同嗎？數列1，2，3與數列3，2，1相同嗎？

（3）數列38，51，2，28，16，16，5，15與數列1，■，■，■，…有何區別？

此處，執教者通過引導學生熟悉的和特殊的簡單問題的研究，進一步獲得對數列相關概念的理解.

問題探究三：通過上述折紙活動，從紙的層數變化而獲得的數列，它的第n項是多少？

生4：第n項是2n.

師：非常好！該數列的第n項可以記作an=2n，這個等式為該數列的通項公式. 一般來說……

問題探究四：（1）能否寫出“一尺之棰”每日剩余部分所得數列的通項公式？

（2）談一談數列與函數的關系.

生5：數列可以視為以正整數N*或是它的有限子集{1，2，3，…，n}為定義域的函數，當自變量的取值順序為從小到大時，所對應的為一列函數值.

設計意圖：操作實踐為學生提供了摸得著的切身體驗，讓學生有了充分的感知，而以上“理解性探究”則把以上單一的個別的活動體驗串聯起來，通過大膽表達闡釋自身的理解和認識. 學生沿著以上問題一路探究下來，強化了對數列問題的感悟，固化了對數列本質的理解. 整個教學過程中，師生之間有效對話，時時合作，在理解的基礎上學習和提升，促進了動態生成的推進.

啟示：此處問題的設計可謂獨具匠心，用問題引領學生在理解概念的基礎上生成自身的看法，學會深入思考后運用自己的語言闡述數學知識，在多角度的思考與敘述中加深對新知的認識，這樣的體驗過程不僅是思維訓練的過程，也是數學素養的訓練過程，讓學生的理解與概念本質靠攏，促進了學生的動態生成.

4. 理解性應用

例1：已知數列{an}的通項公式為an=3n+1.

（1）寫出它的前5項;

（2）寫出它的第2013項;

（3）37是該數列中的項嗎？如果是，是第幾項？

例2：寫出數列的一個通項公式，使得其前4項分別為以下各數：（1）1，■，■，2;（2）-1，■，-■，■.

設計意圖：以上兩個例題的設計滲透了特殊與一般、算法與方程的數學思想，不僅讓學生探到了本課的重點，同時也經歷了這節課難點的研究，讓學生充分理解了“數列是特殊的函數”，培養了學生觀察、分析、探究與歸納等關鍵性能力.

練習1：寫出數列的一個通項公式，使得其前4項分別為以下各數：

（1）1，1，1，1;？搖（2）1，3，5，7;

（3）■，■，■，■;

（4）■，■，■，■.

練習2：已知數列{an}的通項公式為an=■.

（1）寫出該數列的前5項，并作出其圖像;

（2）寫出該數列的第10項;

（3）■是該數列中的項嗎？如果是，是第幾項？

設計意圖：概念的形成是一個循序漸進的過程，只有經歷自然的、階梯式的拓展訓練，才能讓學生更快地認識和理解概念，展現理解的拓展性因素.

啟示：在解題的過程中，學生開展了一系列的探究活動，深化對新知的理解;更重要的是在這個過程中，提升了學生探究問題的能力，發展了學生的核心素養.

基于理解性學習的生態課堂

1. 情境引領是前提

建構主義認為，情境是促進認知的基石，合理而有效的教學情境可以促進學生的“再發現”和“再創造”. 支持理解性學習的課堂應當是帶著興奮與好奇，體驗理性精神的課堂. 執教者以一句切合課題的歷史名言導入課堂，喚醒了學生的愛國熱情，激起了學生的學習欲望，一步步地探究數列這個富有魅力的一串數字背后所蘊含的深刻含義，讓學生在理解的過程中享受探究帶來的愉悅.

2. 體驗中學習是根本

蘇霍姆林斯基曾說：“學生要想牢固地掌握數學，就必須用內心創造與體驗的方法來學習數學.”由此可見，在體驗中學習是學好數學的關鍵所在. 以上學習過程中，教師融合多種教學策略，使學生在深層次的體驗中習得新知，發展能力. 執教教師圍繞一個課題，通過思、說、做等多種方式培養學生的綜合思維和遷移能力，使學生在探究中深入，在合作中發展，在體驗中學習，促進學生數學素養的提升，進一步提高課堂教學的有效性.

3. 在理解性學習中生成生態課堂

生態課堂是著眼于學生的長期發展，著重強調有機整合教師、學生與環境等生態元素，在協調運動后逐步生成的一種促進學生主動發展和健康成長的有效場所[2]■. 理解性學習的生態課堂并非一朝一夕就能形成的，需要教師充分發揮學生的主體作用，關注學生的生命體驗和長期發展，將課堂教學的意義提升到核心素養的思想境界，讓學生在增長學科知識的同時，健全和發展人格.

參考文獻：

[1]? 朱姝. 以生為本，努力構建高中數學生態課堂[J]. 數學學習與研究，2015（01）.

[2]? 陶家捌. 以生態之槳，為數學揚帆——高中數學生態課堂的構建[J]. 新課程（下），2019（05）.