預判指引 事半功倍

常建偉

[摘? 要] 平面解析幾何綜合題綜合性強，運算過程復雜，方法靈活多變. 有的學生在解題過程出現思路受堵，運算煩瑣. 學會借助預判思維指引解題，通過目標預判，明確解題方向;通過方法預判 優化解題策略;通過結果預判，修正解題過程，從而有助于既快又準地解題.

[關鍵詞] 解析幾何;預判思維;圓錐曲線

平面解析幾何綜合題可與函數、方程、不等式、三角、向量、平面幾何等知識交匯考查，往往題目綜合性強，運算過程復雜，方法靈活多變. 解此類題型時，有的學生思維方向容易迷失，無從下手;有的學生方法選擇不當、運算準確性不夠. 若在解題過程中能合理運用預判思維，有助于引領思路，優化解題過程，甚至達到事半功倍的效果. 下面就以解答平面解析幾何綜合題為例，從三個方面談談預判思維在解題中如何合理使用，希望對學生的解題有所啟示.

目標預判，明確解題方向

在解決存在性、探索性等問題時題目未明確給出結論時，我們要充分挖掘題目條件，整體建構好解題思路，采用特殊化、極端化等方法預判出可能結論，將不確定性問題進行目標明確化，再進行結果驗證.

例1：在平面直角坐標系xOy中，橢圓C：■+■=1的左頂點為A，點P，Q是橢圓C上的兩個動點.

（1）如圖1，當P，O，Q共線時，直線PA，QA分別與y軸交于M，N兩點，求證：■·■為定值;

（2）設直線AP，AQ的斜率分別為k1，k2，當k1k2=-1時，證明：直線PQ經過定點R.

試題分析：本題第一問求■·■是定值，可以通過特殊法先預判出定值結果，由于P，Q兩點的運動變化性，不妨取P，Q兩點為短軸的兩端點，則P，Q兩點即為M，N兩點，得■·■=1. 具體寫解題過程時可設點P（x0，y0），Q（-x0，-y0），再將M，N兩點坐標求出，可得■·■=4+■=1. 第二問若采用一般性解法，先設斜參求出直線PQ的方程，然后化簡方程，結合直線系的思想與參數無關進行求解定點，不少學生解題時往往在最后求定點時“卡殼”，因方程復雜，目標定點不明確，無從下手，少數學生的運算基本功扎實、式子處理能力強也能求解.若能結合預判思維，問題便能迎刃而解.由橢圓的對稱性可預判直線PQ過定點，在x軸上，采用特值探求，可令xp=xq或令k1=1，k2=-1，則可求出直線PQ與x軸交點坐標，既直線PQ過定點-■，0，最后用一般化方法驗證. 驗證的過程便體現了解析幾何的思想：用代數的方法研究幾何問題.

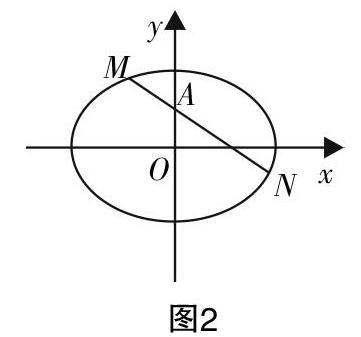
例2：如圖2，過橢圓C：■+■=1內一點A（0，1）的動直線l與橢圓相交于M，N兩點，是否存在與點A不同的定點B，使得對任意過點A（0，1）的動直線l都滿足■·■=■·■？若存在，求出定點B的坐標;若不存在，請說明理由.

試題分析：本題是探索性問題，按常規思路設點直接求解，參數較多，運算復雜，解題很難走到最后.若能打開思維，充分挖掘條件中蘊含的幾何特征，便能預判出可能的結論. 假設點B存在，先取直線l平行于x軸時，由幾何特征知點B在線段MN的垂直平分線即y軸上，再取直線l垂直于x軸，可得點B的坐標只可能是（0，2），然后進行一般性驗證.本題中的一般問題特殊化是破題的關鍵，也是解析幾何直觀性的體現.

方法預判，優化解題策略

解答解析幾何綜合題時為優化解題，降低運算難度，常會面臨著點參、斜參、角參的選擇. 學生在解題時要掌握解析幾何的思維特征和基本思想，根據題設的幾何特征，靈活運用曲線的有關定義、性質，結合自身已有方法經驗選擇合適的參變量、公式、坐標系進行解題預判，從而做出更合理的解題策略選擇.

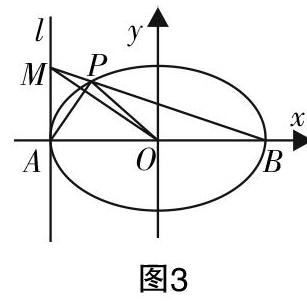
例3：在平面直角坐標系xOy中，已知橢圓C：■+■=1，過橢圓的左頂點A作直線l⊥x軸，點M為直線l上的動點（點M與點A不重合），點B為橢圓右頂點，直線BM交橢圓C于點P，求證：AP⊥OM.

試題分析：問題中要證明AP⊥OM，斜率積和向量數量積兩個角度都可以刻畫垂直關系，但都需求出點P和點M的坐標，此處涉及參數的選擇的問題，可直接設點參求解，也可設斜率參數表示點的坐標. 本題解題方法比較多，如何選擇相對能優化解題過程，減少運算？可做出以下解題方向預判. 若設點參解題，則選擇點M較好，由于點M橫坐標已知，然后求出直線BM與橢圓交點P;若設斜率參解題，則直接將點P通過斜率參表示出來求解;若能進一步發現A，B兩點關于原點對稱，由圓錐曲線“第三定義”知kPA·kMB=kPA·kPB=-■，可直接將直線AP，BM用同一個參數k表示，則本題可得到快速求解.不過還是要提醒學生注意，一旦解題目標確定，預判方法可行，就要堅持算下去，有時堅持比方法更重要.

例4：已知橢圓■+■=1，設直線l：y=kx+m（k≤■）與橢圓C相交于A，B兩點，以線段OA，OB為鄰邊作平行四邊形OAPB，其中頂點P在橢圓C上，O為坐標原點，求|OP|的取值范圍.

試題分析：本題是直線與橢圓的綜合問題，求OP的取值范圍需將點P的坐標表示出來. 在平行四邊形OAPB中，■=■+■，則點P坐標為（xA+xB，yA+yB）. 將直線代入橢圓方程得到關于x的一元二次方程，再結合條件列出|OP|關于k，m的函數，進行求解處理時發現再消參困難，運算煩瑣，容易出錯，甚至解題受阻. 那用設點法能不能處理呢？做出以下預判，將題目條件重新組合，通過點P與點A、點B的坐標關系，聯想到點差法，可將點P的坐標與斜率k的關系找出來，再結合橢圓方程即可求解點P的坐標. 本題答案：■≤OP≤■.

結果預判，驗證解題過程

對解題過程中的一些階段性結果的準確性進行預判，若與解題目標不符，則及時修正調整.

例5：已知圓A的方程為（x+1）2+（y-2）2=20，過點B（-2，0）的動直線l與圓A相交于M，N兩點，Q是MN的中點，直線l與l1相交于點P，直線l1的方程為x+2y+7=0.（1）當MN=2■時，求直線l的方程. （2）■·■是否為定值？如果是，求出其定值;如果不是，請說明理由.

試題分析：有的學生在第一問出現少解情況，錯誤的原因是設直線方程時未考慮斜率不存在的情況. 其實解題過程中通過結果預判可及時發現錯誤.因為點B在圓內部，而弦MN不是直徑，所以這樣的直線肯定有兩條. 我們平時在解題時需要適當停頓，借助幾何直觀，明確算理，多一點思考，便會少出錯.本題的第二問可以采用特殊法進行結果預判檢驗運算的準確性. 本題答案： （1）x=-2或3x-4y+6=0;（2）■·■為定值-5.

例6：在平面直角坐標系xOy中，已知橢圓■+y2=1，左、右兩個頂點分別為A1，A2. 過點D（1，0）的直線交橢圓于M，N兩點，直線A1M與NA2的交點為G，求證：點G在一條定直線上.

試題分析：本題首先可以進行解題目標預判，若過點D的直線交橢圓于M，N關于x軸對稱的M′，N′兩點，則直線A1M′與A2N′的交點為G′，由橢圓的對稱性，可得GG′所在定直線應是與x軸垂直的直線. 由于A1，A2是橢圓左、右頂點，可分別設直線A1M與A2N的方程，并與橢圓聯立方程組求出M，N的坐標，利用M，D，N三點共線寫出兩斜率關系，進一步得到點G的縱坐標是定值.為了驗證運算結果的準確性，可取MN垂直于x軸時將點G的坐標求出驗證. 本題也可以采用先特殊再一般的方法求解，由橢圓的對稱性先預判定直線為x=4，然后設直線MN的方程為x=my+1. 再證明對于任意的實數m，直線A1M與直線A2N的交點G均在直線x=4上.

綜上所述，預判思維在解答解析幾何綜合題的過程中有著顯著的作用，當然預判的結論不一定都是對的，學生需要平時加強知識經驗的積累和方法的總結，以便做出相對準確合理的預判，從而有助于指引解題的方向，優化解題的策略，修正解題的結果，實現既準又快地解題.