典題為例深探究，問題深析重思考

陳碩罡

[摘? 要] 圓錐曲線問題在高考中有著重要的地位，考題設(shè)置有兩大層次：一是立足基礎(chǔ)，考查曲線的基本內(nèi)容;二是立足綜合，考查綜合能力. 近幾年考題側(cè)重考查學(xué)生的探究能力，出現(xiàn)了一些具有探究性的考題，文章以一道圓錐曲線探究題為例，開展問題探究，解后反思，提出相應(yīng)的建議.

[關(guān)鍵詞] 圓錐曲線;探究;定點;面積;最值;思考

圓錐曲線典型問題探究

高考考查圓錐曲線的內(nèi)容較多，涉及基本定義、標(biāo)準(zhǔn)方程、知識關(guān)聯(lián)、幾何性質(zhì)等，往往問題綜合性較強(qiáng)，近幾年的考題逐步側(cè)重考查學(xué)生的探究能力，出現(xiàn)了一些探究性問題，下面對一道圓錐曲線存在性問題進(jìn)行探究.

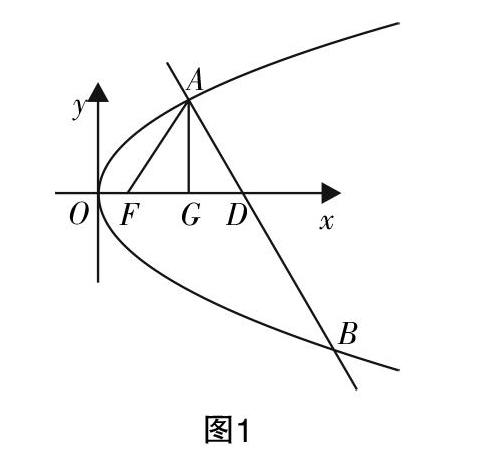
例題：已知拋物線C的解析式為y2=2px（p>0），點F是拋物線C的焦點，點A是曲線上異于原點的一點. 現(xiàn)過點A作直線l，與拋物線C的另一交點設(shè)為點B，與x軸正半軸的交點設(shè)為點D，且有FA=FD.當(dāng)點A的橫坐標(biāo)為3時，△ADF為正三角形，試回答下列問題.

（1）求拋物線C的解析式.

（2）若直線l1與l平行，直線l1與拋物線C的交點有且只有一個，為點E.

①直線AE是否恒過一定點？若不存在，請說明理由;若存在，請求出該點的坐標(biāo).

②△ABE的面積是否存在最小值？若存在，請求出該最小值;若不存在，請說明理由.

思路點撥：本題目為高考常見的圓錐曲線壓軸題，以拋物線為背景，考查解析式求解，探究直線過定點，探究三角形面積的最小值. 問題探究性極強(qiáng)，需要綜合運用圓錐曲線的相關(guān)知識及探究方法. 例題設(shè)置了兩大問，下面逐問探究.

（1）該問求解拋物線C的解析式，主要是求解析式中p的值，可設(shè)出交點F的坐標(biāo)，利用條件FA=FD，根據(jù)拋物線的定義構(gòu)建方程;

（2）該問分為兩個小問，第①問探究直線AE是否經(jīng)過定點，總體思路是設(shè)出點A和D的坐標(biāo)，求得直線AB和l1的方程，然后聯(lián)立直線l1與拋物線C的方程，從而可確定點E的坐標(biāo)，得到直線AE的方程，通過對直線AE的方程簡化即可論證是否經(jīng)過定點.

第②問探究△ABE的面積是否存在最小值，屬于曲線與幾何的綜合探究題，利用面積公式構(gòu)建三角形的面積模型，將其轉(zhuǎn)化為關(guān)于坐標(biāo)參數(shù)的面積函數(shù)，結(jié)合函數(shù)性質(zhì)或不等式性質(zhì)論證是否存在面積最小值.

過程解析：（1）根據(jù)拋物線C的解析式可將焦點F的坐標(biāo)表示為■，0，可設(shè)點D的坐標(biāo)為（t，0）（t>0），則線段FD的中點坐標(biāo)為■，0.已知FA=FD，根據(jù)拋物線的定義可得3+■=t-■，可解得t=3+p或t=-3（舍去），中點G與點A的橫坐標(biāo)相等，即■=3，可解得p=2，所以拋物線的解析式為y2=4x.

（2）①由（1）問可知焦點F（1，0），設(shè)點A（x■，y■）（x■·y■≠0），點D（x■，0）（x■>0）.由于FA=FD，則x■-1=x■+1，解得x■=x■+2，則D（x■+2，0），由點A和D的坐標(biāo)可得直線AB的斜率為k■=-■，又知k■=k■，則直線l■的方程可以表示為y= -■x+b，與拋物線的解析式聯(lián)立可得y2+■y-■=0，由Δ=0，可得b=-■. 設(shè)點E的坐標(biāo)為（x■，y■），則有x■=■，y■= -■. 當(dāng)y■≠4時，可將直線AE的方程表示為y-y■=■（x-x■），結(jié)合y■=4x■可整理為y=■x-1，顯然直線AE恒過點F（1，0）;當(dāng)y■=4時，可將直線AE的方程表示為x=1，顯然同樣恒過點F（1，0）. 綜上可知直線AE恒過一定點，且定點坐標(biāo)為（1，0）.

②該問探究△ABE面積的最小值，可將三角形視為以AE為底、點B為頂點的三角形，則其面積可以表示為S△ABE=■AE·d（其中d表示頂點B到底邊AE的距離）.

由①問可知直線AE過定點F（1，0），則AE=AF+FE=x■+■+2，設(shè)直線AE的方程為x=my+1，點A位于直線AE上，則有m=■.設(shè)點B的坐標(biāo)為（x■，y■），整理直線AB的方程可得x=-■y+2+x■，代入拋物線方程可得y2+■y-8-4x■=0，可求得y■=-y■-■，x■=■+x■+4. 點B到直線AE的距離可以表示為d=■=4■+■，所以S△ABE=■AE·d=■x■+■+2·4■+■=2■+■3≥16，當(dāng)且僅當(dāng)x■=■，即x■=1時等號成立，所以△ABE的面積存在最小值，且最小值為16.

關(guān)于問題的解后思考

上述是對一道圓錐曲線問題的探究過程，其中第（2）問的兩小問具有一定的代表性，下面對其進(jìn)一步反思.

1. 考題突破的關(guān)鍵步驟

題目是高考常見的圓錐曲線問題，其核心之問為第（2）問的兩小問，分別探究直線過定點和面積的最值. 其中第①問的關(guān)鍵一步是確定點E的坐標(biāo)，需要結(jié)合題目中的條件將其表示，上述設(shè)出點A的坐標(biāo)，采用信息直譯的方式，按照“直線AB斜率→直線l方程→直線l■方程→點E坐標(biāo)”的思路完成構(gòu)建. 而第②問突破的關(guān)鍵有兩個：一是如何構(gòu)建三角形的面積模型，轉(zhuǎn)化為面積函數(shù);二是如何研究函數(shù)的最值. 上述充分利用了點到直線的距離公式及不等式的性質(zhì)來完成上述關(guān)鍵點的突破.

2. 考題突破的解法啟示

總體而言，上述圓錐曲線考題為存在性探究題，從直線過定點和面積最值的探究過程來看，數(shù)形結(jié)合是突破的有效策略，采用假設(shè)驗證方法是突破的基本思路，將問題轉(zhuǎn)化為關(guān)于核心變量的數(shù)式則是解析的目標(biāo). 其中核心變量的設(shè)定將直接關(guān)系到問題數(shù)式構(gòu)建的復(fù)雜度，存在性問題的核心在于求出其中的未知量，故設(shè)定核心要素時可以此為依據(jù).另外核心變量求解時可采用如下方法：①直接利用其中的條件和輔助變量表示，②聯(lián)立核心變量與已知條件，構(gòu)建求解方程，利用方程思想來表示核心變量.

3. 考題變式的拓展方向

開展考題變式是提升學(xué)生思維的重要方式，同時可引導(dǎo)學(xué)生深刻認(rèn)識考題，以上述試題為例，具有多個拓展方向，除了可以對其最值進(jìn)行逆向思維命題外，還可以結(jié)合三角形的周長、角度特性進(jìn)行變式.

變式1：當(dāng)△ABE的面積為16時，求點A的坐標(biāo).

解析指導(dǎo)：該變式與原問題突破思路一致，構(gòu)建面積模型，轉(zhuǎn)化為關(guān)于點坐標(biāo)參數(shù)的面積方程，解方程即可.

變式2：△ABE是否可以為直角三角形？若可為直角三角形，試求點A的坐標(biāo);若不可以，請說明理由.

解析指導(dǎo)：直角三角形中一內(nèi)角為90°，條件沒有設(shè)定直角需要對其加以討論，構(gòu)建方程的依據(jù)有如下幾種：①勾股定理，②交叉直線斜率之積為-1，③向量之積為0. 從簡化過程角度來看建議采用后兩種構(gòu)建方式.

探究性問題的教學(xué)建議

1. 引導(dǎo)學(xué)生明晰探究性問題的指向

圓錐曲線探究題能夠全面考查學(xué)生的知識水平和思維能力，因此備受出題人青睞，而在實際學(xué)習(xí)時需要引導(dǎo)學(xué)生明晰探究性問題的命題指向，包括基本形式、考查內(nèi)容、突破思路等. 例如探究性問題常出現(xiàn)“是否”“有且只有”“探究”等詞匯，主要考查曲線的位置關(guān)系、圖形性質(zhì)、向量數(shù)量積、數(shù)式變形等內(nèi)容，突破時可采用假設(shè)論證的思路. 解題教學(xué)中不僅應(yīng)重視問題轉(zhuǎn)化的過程，還應(yīng)注重引導(dǎo)學(xué)生體會探究性問題的解析思路，幫助學(xué)生提升探究能力.

2. 引導(dǎo)學(xué)生形成數(shù)形結(jié)合的策略

圓錐曲線題最為顯著的特點是融合了“數(shù)”與“形”，即將曲線解析式與圖像有效地融合為一體，從數(shù)形角度來突破是最基礎(chǔ)的策略，因此問題探究的過程有必要根據(jù)題意來繪制草圖，探索圖像結(jié)構(gòu)，挖掘隱含信息，在此基礎(chǔ)上排除干擾，提取圖形，合理討論. 例如上述考題的最后一問探討三角形的面積，關(guān)鍵的一步是構(gòu)建面積模型，結(jié)合圖像來加以分析很容易確定模型構(gòu)建的方式. 教學(xué)中要向?qū)W生傳達(dá)數(shù)形結(jié)合解析問題的策略，使學(xué)生深刻體會數(shù)形結(jié)合的思想內(nèi)涵，掌握數(shù)形結(jié)合方法的解析技巧.

3. 引導(dǎo)學(xué)生重視解后思考的變式

對考題進(jìn)行拓展變式有助于學(xué)生全面認(rèn)識問題，總結(jié)解題方法，拓展數(shù)學(xué)思維.解題教學(xué)幫助學(xué)生貫通思路后，學(xué)生對問題的脈絡(luò)有了初步的了解，但思維仍停留在考題本身，并不能完全認(rèn)清問題的結(jié)構(gòu)，更無法把握其中的關(guān)鍵步驟和核心解法，此時需要教師合理設(shè)置變式問題，引導(dǎo)學(xué)生進(jìn)行解后反思.在反思過程中重視對思路、解法的整合，將問題上升到類題層面，促進(jìn)學(xué)生形成完善的解題策略，促進(jìn)數(shù)學(xué)思維的發(fā)展.