基于Hermite插值改進的軌跡修正濾波算法

丁志偉 陳澤宇 馬夢園 張正軍

摘? ?要：借助移動物體軌跡上標定的真實值點的位置信息和方向信息，構造分段三次Hermite插值函數，對標準卡爾曼濾波和標準粒子濾波的狀態方程進行修正，得到兩種改進濾波模型，解決了標準濾波算法中狀態方程不能準確刻畫物體實際運動軌跡的問題。在實驗分析中對定常速曲線運動物體的位置坐標進行濾波修正，位置坐標的均方誤差分析表明，卡爾曼濾波算法和粒子濾波算法的濾波效果均有改善，其中卡爾曼濾波算法在精度上明顯提高。此外，真實值點數量的靈敏度分析的結果表明，在目標軌跡上取少量且關鍵的點作為真實值點即可達到明顯的修正效果。

關鍵詞：卡爾曼濾波;粒子濾波;真實值;Hermite插值

中圖分類號： TN713;P228.4? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A

Implementing Filtering Algorithm Refined

by Hermite Interpolation in Track Revision

DING Zhi-wei?，CHEN Ze-yu，MA Meng-yuan，ZHANG Zheng-jun

（School of Science，Nanjing University of Science and Technology，Nanjing，Jiangsu 210094，China）

Abstract：Through the position and direction information of the real value points on object track，a piecewise cubic Hermite interpolation function is constructed to modify the state equation of standard Kalman filter and standard particle filter. The state equation in standard filter algorithm can describe the actual trajectory of specific object more accurately. In the experimental analysis，the track of the object with constant velocity in curvilinear motion is revised. The mean square error of the position coordinates demonstrates that the improvement of Kalman filter algorithm and particle filter algorithm is practical. Moreover，Kalman filter algorithm is improved more significantly in position accuracy. Besides，the sensitivity analysis about the number of real points shows that a proper number of key points on the target track can be regarded as real points to achieve expected accuracy.

Key words：Kalman filter;particle filter;real value;Hermite interpolation

隨著衛星定位技術和計算機技術的發展，移動物體軌跡的應用也日益廣泛，如車輛異常狀態的分析、車輛的動態軌跡預測等[1]。但由于 GPS 定位受到多種誤差的影響[2-3]，極大限制了高精度實時定位的應用。

在動態軌跡修正領域，常用的技術有標準卡爾曼濾波和標準粒子濾波。雖然它們的可行性已經得到研究的驗證[4-5]，但在實際應用中濾波算法會產生精度不高、濾波發散等問題。當前國內外針對標準濾波算法的不足，已經提出了一系列的改進算法。

在提高卡爾曼濾波算法的精度方面，學者們從不同角度提出基于卡爾曼濾波的改進算法，如結合最小二乘法的卡爾曼濾波算法[6]，運用位置差分方法提出帶速度約束條件的卡爾曼濾波算法和擴展卡爾曼濾波等[7-8]。還有學者通過修正狀態方程中的誤差項以改善濾波效果[9]。為了避免濾波發散，有學者提出一種漸消因子改進算法，實現卡爾曼濾波的自適應[10]。作為粒子濾波算法的主要缺陷，粒子退化問題受到學者的廣泛討論與研究，解決該問題最有效的方法是選擇好重要性概率密度函數或采用重采樣方法。在提高粒子濾波實時性的方面，有學者提出自適應粒子濾波（APF）和實時粒子濾波（RTPF）等改進算法[11]。

標準卡爾曼濾波方法中使用的線性模型不能刻畫物體的某些復雜曲線運動，雖然一些基于非線性模型的改進卡爾曼濾波算法和部分改進的粒子濾波算法能夠解決該問題，但這些方法較為復雜，且無法達到某些應用領域的要求。因此，需要一種較為簡便的濾波方法，繼續使用線性模型來描述動態運動，并盡可能縮小誤差范圍，保證濾波的效果。

提出了一種基于真實值點構造分段三次Hermite插值函數的改進思路，將其運用于標準卡爾曼濾波和標準粒子濾波，分別得到兩種改進的濾波算法。該類算法通過Hermite插值函數近似移動物體的真實軌跡，達到濾波預測值更接近真實情況的目的。實驗結果表明，卡爾曼濾波算法和粒子濾波算法的濾波效果均有改善，其中卡爾曼濾波的改進效果尤為顯著。與先前的研究相比，上述方法簡便易行，對于移動物體的軌跡修正精度有顯著提高。

1? ?移動物體的運動學模型

在BJ-54坐標系下，考慮物體的定常速曲線運動模型，以物體的位置和速度作為狀態變量，并假定系統噪聲和測量噪聲均為高斯白噪聲。設物體的狀態向量為Xt = [xt? ?yt? ?vx，t? ?vy，t]T。其中，xt、yt分別為t時刻物體所在位置的BJ-54橫坐標、縱坐標;vx，t、vy，t分別為t時刻物體在橫坐標軸、縱坐標軸方向上的速度。

此時，狀態方程為：

式中，At|t-1為從t-1時刻到t時刻的狀態轉移矩陣。

狀態轉移矩陣和噪聲驅動矩陣分別為[12]：

式中，ωt為t時刻目標物體的角速度;dT為GPS采樣的時間間隔。

觀測方程為：

Zt = HXt + νt（4）

式中，Zt為觀測向量;H為測量矩陣，H = I4 為4階單位矩陣。

2? ?標準濾波模型及算法

2.1? ?標準卡爾曼濾波算法

標準卡爾曼濾波算法是基于狀態空間的一套遞推濾波算法，它主要包括狀態方程和觀測方程。標準卡爾曼濾波過程主要由以下公式組成：

式中，At|t-1為狀態轉移矩陣;[^][X]t為t時刻狀態向量的濾波估計值;[^][P]t為t時刻誤差的協方差矩陣;Q = σ2

uBBT為系統噪聲的協方差矩陣;R為測量噪聲的協方差矩陣;Kt為t時刻的卡爾曼濾波增益值。

2.2? ?標準粒子濾波算法

標準粒子濾波算法是一種基于貝葉斯理論和蒙特卡羅方法的統計濾波算法。其基本思想是先在狀態空間中產生一組加權隨機樣本（粒子），然后在測量數據的基礎上通過調節粒子的權重大小來獲得服從實際分布的樣本，并以樣本均值作為系統狀態的估計值。

粒子濾波的具體實現步驟如下[11，13]：

Step1：初始化k = 0，采樣xi

0 ～ p（x0），即根據分布p（x0）采樣得到xi

Step2：重要性權值計算。設定k ：= k + 1，采樣xi

重要性權值計算如下：

Step5：判斷是否結束，若是則退出本算法，若否則返回Step2。

3? ?改進的濾波算法

3.1? ?改進的思路

上述兩種濾波算法均利用狀態轉移矩陣At|t-1刻畫移動物體從t-1時刻到t時刻的狀態變化，并結合實際觀測值Zt，求得t時刻濾波預測值[^][X]t，再讓 [^][X]t參與下一步的迭代。但在實際應用中路況復雜，運動學公式無法準確描述移動物體的實際運動軌跡，從而經濾波后得到的軌跡與實際軌跡有較大偏移。考慮到應用中存在上述不足，本文提出一種改進思路應用于濾波算法，用作移動物體的軌跡修正。事實上，物體的移動軌跡上存在一些關鍵點，如連續轉向點。而這些轉向點一般存在于特殊路段如十字路口、高速的匝道等，該處經緯度可以事先精確測量。

基于上述考慮，給定移動物體軌跡上的n個已知經緯度坐標的真實值點列S = {Pi|i = 1，2，…，n}，利用分段插值方法做出一段曲線，再將由運動學公式計算得到的t時刻位置的橫坐標xi代入插值曲線方程，可以計算出預測的真實值點的縱坐標yi*。然后，對（xi，yi）和（xi，yi*）經過加權修正得到（xi，[y][～]i）以減少運動學公式利用帶來的誤差。最后，將（xi，

[y][～]i）作為修正后的理論值中間變量代入濾波過程，可求得修正后的濾波預測值（[x][^]i，[y][^]i）。

改進濾波算法的具體思路見圖1。

3.2? ?真實值點列的選擇

針對定常速曲線運動情形，主要選取在方向發生較大變化的拐點、周圍存在較多的隨機因素的路口等位置。Hermite插值方法需要區間端點的位置和導數值，本文用待求點的一階差商作為該點導數值的近似替代，在實際算法中，只需再一個構造輔助的真實點列[S][～] = {[P][～]i|i = 1，2，…，n}。

對Pi和[P][～]i的坐標作差商，將得到的結果作為真實值點Pi的導數值，用于插值函數的構造。實際應用中可以借助于速度傳感器等設備搜集一階導數信息，不必依賴真實值點。只是在本研究中受限于儀器設備，故作該處理，因此后文在統計所需真實值點的數目時，未將輔助點數目納入其中。引入真實值點列具有重要意義：根據點的選取原則，真實值點列為軌跡上關鍵的，或者測量中容易發生偏移的位置。那么，運用點列信息后就可以減少點列附近測量數據的偏移。在上述方法中，還需指出，僅利用插值函數修正理論值中間變量的位置信息，對于速度和方向沒有改動。

3.3? ?分段三次Hermite插值

設真實軌跡函數為fi（x），i = 1，2，…，n，相鄰兩個真實值點Pi和Pi+1的BJ-54坐標為（xi

式中，α1和α2為權重因子，分別衡量對狀態方程和真實值點的依賴程度。當α1 = 1，α2 = 0時，退化為標準濾波算法。一般地，α1和α2在（0，1）內取值。

3.4? ?Hermite-KF算法（HKF）

HKF算法過程主要由以下公式組成：

式中，Xt*為修正后的理論值，其它符號的含義同前。

HKF的主要步驟如下：

Step1：參數值的初始化：給定初始狀態X0，誤差協方差矩陣初值P0 = I4，其中I4為四階單位矩陣;系統噪聲的協方差矩陣Q = 10-3 × BBT;測量噪聲的協方差矩陣R為對角矩陣，可由單點定位誤差的方差和速度的測量方差得到;

Step2：狀態更新：根據t - 1時刻的預測狀態[^][X]t 結合狀態方程計算第t時刻的狀態Xt;

Step3：加權修正：根據第二步中Xt確定位置區間和運動方向，尋找對應的插值區間，并運用Hermit插值法計算插值函數的函數值H（Xt），用算術平均修正位置信息，得到修正后的狀態量Xt*;

Step4：誤差更新：根據第t - 1時刻的過程預測誤差[^][P]t估計t時刻的過程預測誤差[P][～]t;

Step5：增益計算：計算卡爾曼增益Kt;

Step6：濾波預測：結合實際觀測值計算系統最優估算值[^][X]t;

Step7：誤差預測：計算系統當前時刻的系統預測誤差[^][P]t。

3.5? ?Hermite-PF算法（HPF）

HPF算法的狀態方程和觀測方程分別為：

Xt* = F（At|t-1 [^][X]t-1 ） + But - 1

Zt = HXt + νt（10）

其余迭代步驟同前。

4? ?實驗與分析

4.1? ?實驗設計

實驗選取ATGM332D雙模接收機作為GPS數據接收工具，結合自行編寫的BD-GPS數據采集系統對衛星數據進行解碼，獲取經緯度、海拔高度及速度等信息。在南京奧體中心進行實地實驗，對定位數據分別采用KF、HKF、PF、HPF進行濾波。實驗結果以均方根誤差作為評價標準，衡量濾波算法的改善效果，并對真實值點列個數進行靈敏度分析。

改進的濾波算法中真實值點列經緯度坐標的確定：在軌跡上取12個關鍵點，每個點用GPS接收機采集1000個經緯度定位數據，后進行單點濾波[15]，將濾波的平均值作為真實值對應的經緯度。

4.2? ?數據預處理

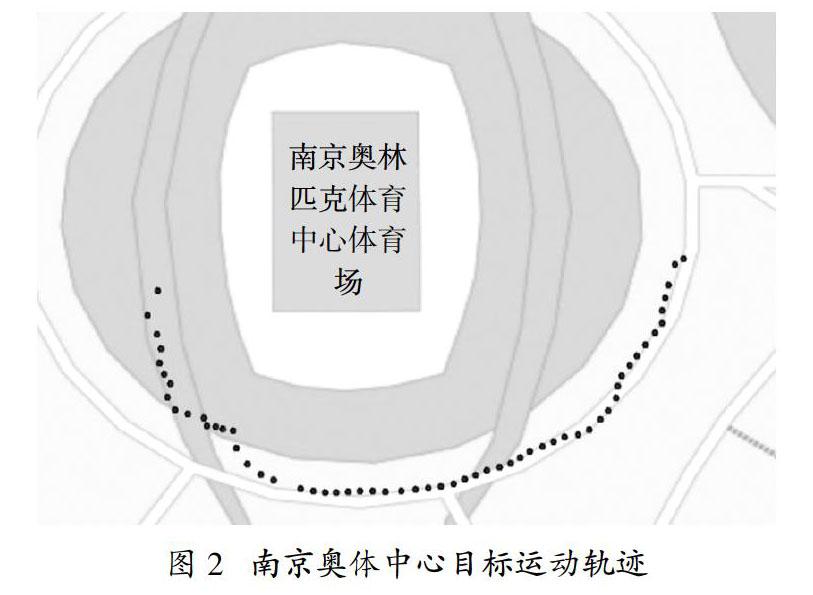
首先剔除野點。由于運動模型中采用XY坐標而非經緯度，因此需要進行坐標變換[16-17]。圖2是南京奧體中心經緯度數據轉換后的物體運動軌跡。

4.3? ?實驗結果及分析

4.3.1? ?濾波算法的效果比較

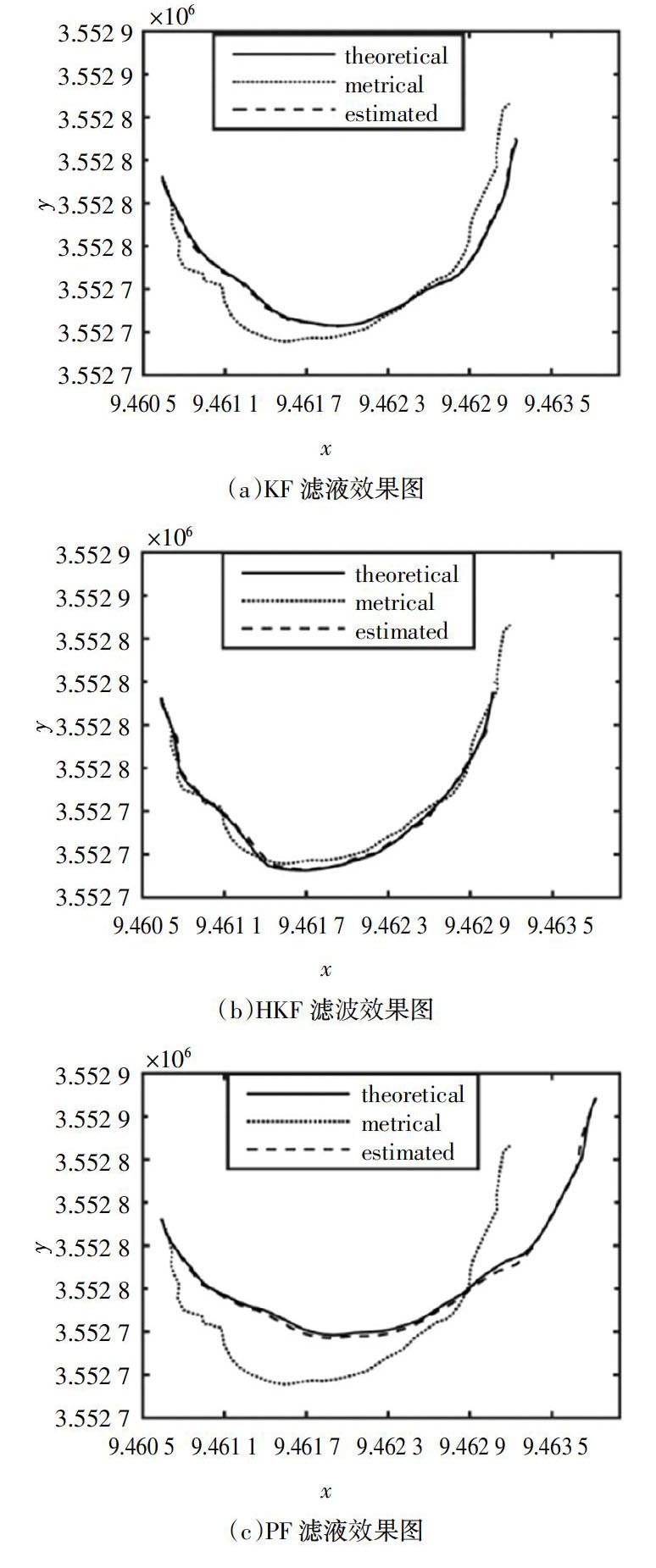
在定常速曲線運動情形下，分別利用KF、HKF、PF、HPF對定位數據進行修正，這里借助的真實值點的數目為7。

圖3中的a，b，c，d分別為KF、HKF、PF、HPF的濾波效果圖。圖中theoretical表示理論公式計算得到的坐標;metrical表示實際測量值;estimated表示濾波估計的位置坐標。不難看出，相比于標準算法，兩種改進濾波算法的理論值與實際值更加接近，這是引入真實值點陣修正后的效果，更加準確地刻畫實際測量中的道路軌跡，進而可以達到讓濾波更為準確的目的。

進一步地，將濾波結果同真實值相比，分別做出兩種濾波下x坐標和y坐標的誤差圖，見圖3中e，f，g，h。可以看到，HKF的誤差較KF有顯著減小;HPF在y方向上誤差較PF有顯著減小，在x方向上有些許增大。總體來說，兩種算法的誤差均有減小。這一點也可以從兩種濾波方法下位置坐標的均方根誤差中看出，根據均方根誤差計算式：

RMSEx = ，（11）

RMSEy = .（12）

得在四種濾波下的x、y方向上的均方誤差，見表1。

由表1知，卡爾曼濾波算法和粒子濾波算法均有改進。

4.3.2? ?靈敏度分析

對于改進的濾波方法，真實值點的數量與誤差減小之間需要進行權衡。如果所需要的點數過多，那么前期采集真實值的工作量就變得龐大，改進濾波方法的實用價值自然也就不大。因此，以下針對真實值點的個數進行靈敏度分析。

圖4是HKF和HPF在x、y方向上偏移量示意圖，橫坐標表示時間，縱坐標表示對應時刻真實點和濾波預測點坐標的偏移量。對于HKF，不同的真實值點數對于x、y方向的誤差影響較小;對于HPF，除了在5個真實值點時由于真實值點數量太少導致y坐標誤差較大外，借助多于8個真實值點時x、y方向上誤差均在（-5，15）內波動，這說明真實值點的數量對于誤差的減小效果并不敏感。

計算在不同真實值點數下兩種改進濾波的均方根誤差，見表2和表3。結果表明，隨著真實值點數目的增加，均方根誤差總體上呈減小趨勢，但效果不明顯，這表明在運用中，只需要依賴較少的真實點，就可以達到減小定位誤差的目的。

研究還表明，當真實值點取在道路上的關鍵點，比如軌跡的起始點、終點和拐點的時候，濾波效果更好，均方根誤差更小。針對選用7個真實值點

研究還表明，當真實值點取在道路上的關鍵點，比如軌跡的起始點、終點和拐點的時候，濾波效果更好，均方根誤差更小。針對選用7個真實值點時，在對所取點的位置進行分析后得出，選取關鍵點可以顯著降低誤差，效果甚至優于借助更多的真實值點，改進卡爾曼濾波的效果見表4。

表4? ?不同取點位置下HKF的誤差比較

[點列數 7點 7點關鍵點 RMSEx /m 4.488 8 4.487 5 RMSEy /m 3.498 2 3.480 2 ]

5? ?結? ?論

對標準濾波算法進行優化，在狀態方程中融入由真實值點列構成的插值多項式，根據物體的運動方式，對插值多項式和運動學公式選取不同的權值，改進狀態方程，使得對下一時刻狀態的估計更加精確。實驗結果表明，借助于移動物體軌跡上較少的關鍵位置的真實點，改進卡爾曼濾波算法和改進粒子濾波算法可以實現對一段軌跡的經緯度的修正，且在精度上相比標準算法得到了提高。在實際應用中，只需事先在計劃軌跡上標定真實點，以后無需標定。該方法成本低、效果好。但是受限于時間和經費，沒有進行大量的實驗，僅僅對定常速曲線運動情況進行了分析，對于更一般的運動形式有待進一步分析。

參考文獻

[1]? ? 陳志軍，吳超仲，呂能超，等. 基于改進三次Hermite插值的車輛時空軌跡重構研究[J]. 交通信息與安全，2013，31（6）：43-46.

[2]? ? ELLIOT D K，CHRISTOPHER J H. GPS原理與應用[M]. 寇艷紅，譯. 北京：電子工業出版社，2007.

[3]? ? 劉基余，李征航，王躍虎，等. 全球定位系統原理及應用[M]. 北京：測繪出版社，1993.

[4]? ? 劉嬋媛，陳國光. 基于GPS的卡爾曼濾波技術研究[J]. 彈箭與制導學報，2006，26（4）：110-112.

[5]? ? 張塹，高天德. 基于GPS的動態目標定位濾波方法[J]. 計算機仿真，2012，29（5）：319-321，337.

[6]? ? 陳鵬，錢徽，朱淼良.基于加權最小二乘的卡爾曼濾波算法[J]. 計算機科學，2009，36（11）：230-231，257.

[7]? ? 陳寶遠，孫宇思，陳光毅，等. 一種基于卡爾曼濾波的動態目標GPS定位算法[J]. 哈爾濱理工大學學報，2016，21（4）：1-6.

[8]? ? 林雪原，駱卉子，范文強. 一種改進的GPS動態定位濾波方法[J]. 海軍航空工程學院學報，2010，25（4）：361-364.

[9]? ? 宋迎春. 動態定位中的卡爾曼濾波研究[D]. 長沙：中南大學，2008.

[10]? 蔡艷輝，程鵬飛，李夕銀.用卡爾曼濾波進行GPS動態定位[J]. 測繪通報，2006（7）：6-8.

[11]? 朱志宇. 粒子濾波算法及其應用[M]. 北京：科學出版社，2010.

[12] ACHUTEGUI K，RRODAS J，ESCUDERO C J，et al. Bayesian filtering methods for target tracking in mixed indoor/outdoor environments[C]. International Conference on Mobile Lightweight Wireless Systems，2012：169-185.

[13]? 胡洪濤，敬忠良，李安平，等. 非高斯條件下基于粒子濾波的目標跟蹤[J]. 上海交通大學學報，2004，38（12）：1996-1999.

[14]? 關冶，陸金甫.數值分析基礎（第二版）[M]. 北京：高等教育出版社，2010.

[15]? 孫罡，王昌明，張愛軍. GPS靜態單點定位的濾波算法比較[J]. 南京理工大學學報（自然科學版），2011，35（1）：80-85.

[16]? 王解先，王軍，陸彩萍. GPS測定坐標轉換至地方坐標[J]. 全球定位系統，2003，28（4）：7-10.

[17]? 蔣小軍，宋占峰，吳清華. 地方獨立坐標系與WGS-84坐標系轉換方法及應用[J]. 鐵道勘察，2010，36（4）：8-10，13.