基于離散對數的廣義數字簽名算法研究

丁家琳

摘? ? 要： 回顧了Ren-Harn的廣義環簽名算法，但Ren-Harn的廣義環簽名并不能滿足可轉化性的定義。以Ren-Harn的方案為基礎，提出了基于時間戳的Ren-Harn算法，即在算法中引入時間戳變量，同時構造出雙線性映射的單向陷門函數。通過環簽名算法的驗證，改進方案不僅嚴格滿足可轉化性的定義，而且具有很好的安全性。在保障真實簽名者對于環簽名的獨創性，防止信息的惡意篡改等方面有很深遠的影響和意義。

關鍵詞：環簽名;可轉化性;合成函數;廣義環簽名;時間戳

中圖分類號：TP751 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A

Study of General Digital Signature Algorithm Based

on Discrete Logarithm

DING Jia-lin?

（Network Security Division，Liaoning Province Meteorological Information Center，Shenyang， Liaoning 110166，China）

Abstract： The Ren-Harn generalized ring signature algorithm is reviewed， but the Ren-Harn generalized ring signature can't meet the definition of the transformation. On the basis of Ren-Harn scheme， the new Ren-Harn algorithm based on time stamp is proposed， and the variable of the time stamp in the algorithm is introduced. At the same time， the one-way trapdoor function of bi-linear mapping is constructed. Through the verification of ring signature algorithm， the improved scheme not only satisfies the definition of convertible strictly， but also has good security. It has a far-reaching influence and significance in the protection of the real signer for original ring signature， preventing the information from malicious tampering.

Key words：ring signature;convertibility;combining function;generalized ring signature;time stamp

2008年，Ren和Harn首次提出了基于ElGamal簽名方案的廣義環簽名方案[1]。然而，王華群等人通過對廣義環簽名的密碼分析，最后證明Ren和Harn的方案并不能滿足環簽名的可轉化特征[2-3]。因為每一個環成員都有能力宣稱是自己產生的簽名。但這并不意味著Ren和Harn的方案徹底失敗了，廣義環簽名的提出本身就對密碼學的發展起到了很大的促進作用。文中對Ren和Harn的方案加以改進，提出了基于時間戳的Ren-Harn算法，最終使得廣義環簽名滿足可轉化性。改進后的方案能夠保障只有真實的簽名者才有能力向驗證者證實簽名是自己生成的。

1? ?基礎預備知識

對一些符號進行說明并簡要闡釋一些基本定義。

假定Bob想為信息m產生一個包含n個環成員（B1，B2，…，Bn）的環簽名，其中Bob為Bs（1≤s≤n）。每一個環成員都擁有一個公鑰-私鑰對（Pi，Si）。

1.1? ?基本定義

定義1：（環簽名）環簽名方案是由以下兩大算法組成的：

環簽名算法（m，P1，P2，…，Pn）：已知信息m和n個環成員的公鑰P1，P2，…，Pn，真實的簽名者Bs能夠使用自己的私鑰Ss和其他環成員的公鑰生成一個環簽名σ。

環驗證算法（m，σ）：已知信息m和環簽名σ，又由于各個環成員的公鑰都是公開的，驗證者完全能夠判斷（m，σ）是否是一個有效的簽名。

定義2：（可轉化的環簽名）如果一個環簽名還包含以下兩大算法就被稱作可轉化的環簽名：

環轉化：真實的簽名者能夠向驗證者提供不可抵賴的證據以證實環簽名是由自己而不是由其他的環成員產生的。

環轉化驗證：給定一個環簽名（m，σ′）和一組環成員的公鑰集合（P1，P2，…，Pn），驗證者能夠證實該簽名是不是有環成員Bs產生的。

對于可轉化的環簽名有以下三點安全要求：

（1）簽名者匿名性：驗證者能夠正確猜出簽名者身份的概率僅為1/n;

（2）不可偽造性：任何一個非環成員都不可以偽造簽名;

（3）對于非真實簽名者的不可轉化性：任何一個環成員Bi（i≠s），都無法將環簽名轉化為普通的數字簽名。

定義3：（合成函數）合成函數Ck，v（y1，y2，…，yn）把一個密鑰值k，一個初始化值v和一組任意值y1 = g1（x1），y2 = g2（x2），…，yn = gn（xn）∈{0，1}b當做輸入，其中g1，g2，…，gn為陷門函數。它最終輸出一個值z∈{0，1}b。因此，對于任意給定的k，v，s（1≤s≤n）和任意輸入的定值yi（i≠s），合成函數相當于一個從ys到z的一對一映射。而且，這個映射還是高效可執行的。但是如果不知道私鑰和陷門函數g1，g2，…，gn的反函數的話，將很難進行對于x1，x2，…，xn的驗證方程。

參考文獻[1]中的合成函數：

2? ?回顧Ren-Harn的廣義環簽名方案

首先回顧文獻[8]中的Ren-Harn的廣義環簽名方案（以下簡稱Ren-Harn方案），然后給出了該方案的不足，即該方案并不能滿足Ren-Harn所聲稱的可轉化性[2]。

2.1? ?Ren-Harn方案

2008年，Ren-Harn提出了基于ElGamal簽名方案的環簽名，他們把它稱為廣義環簽名，并聲稱該方案是可轉化的。

在一個ElGamal簽名方案中，p是一個大素數，g是Zp中的生成元，并且p、g被公開。簽名者為自己隨機選取私鑰d∈Zp-1，那么公鑰就可以通過e = gdmodp計算得出，私鑰d需要保密。

假如m是需要被簽名的信息，簽名者隨機從Zp-1中選取一個一次性秘密值l并且計算出α =? glmodp，β = （m - dα）l-1mod（p-1）。這樣我們就可以把（α，β）當做信息m的有簽名，簽名的有效性可以通過驗證式gm = eααβ來進行判斷。

在Ren-Harn環簽名方案中，定義gi（ai，bi） = （mi，αi，βi），這樣會很容易計算擴展陷門置換gi的逆。但是如果我們將gi與工程映射pi（在這里有pi（mi，αi，βi） = mi）結合在一起，那么將很難計算fi = pi·gi的逆。事實上，fi是基于雙線性映射Zp-1 × Z*p-1 →Zp-1的單向陷門函數[3]。通過圖1更有助于我們理解fi、pi、gi三者之間的關系：

在Ren-Harn方案中，不再需要對稱加密算法E，但是我們同樣需要一個被公共定義的抗碰撞的hash函數h。下面，我們將呈現Ren-Harn方案中的環簽名算法和環驗證算法：

環簽名算法：（m，e1，e2，…，en，ds，s）：m為將要被簽名的信息，ds為簽名者的私鑰，e1，e2，…，en為各個環成員的公鑰，簽名者按如下步驟計算環簽名：

1.選取密鑰值：簽名者Bs首先計算對稱密鑰值k = h（m），k值在這里其實就是信息m經過hash函數處理后的摘要值。簽名者可以直接對k進行簽名。

2.隨機選取膠值：簽名者隨機選擇一個初始化值v∈Zp。

3.為信息mi生成偽造簽名（αi，βi）：真實的消息簽名者任意選擇ai∈Zp-1，bi∈Z*p-1（其中i = 1，2，...，n，i≠s），那么簽名（αi，βi）可以從獲得gi（ai，bi） = （mi，αi，βi）獲得。

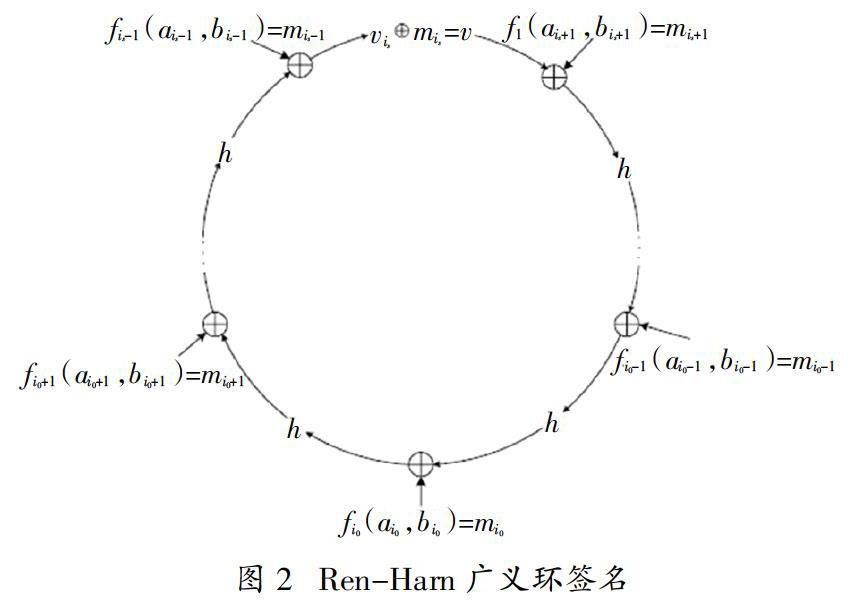
4.求解m：假設真實的簽名者所簽名信息的下標為is。令

上面所有式子里面出現的下標都屬于Zn。因此，我們有v= v。為了形成一個環，令vm = v，這樣可以得到m= v v，如圖2所示。

5.利用簽名者的陷門信息對m簽名[4]：真實的簽名者Bs首先隨機選擇l∈Z *p，但要求l和p - 1互素。這樣m的簽名為（αi，βi） = （glmodp（m- diαi）l-1mod（p-1）。

6.輸出環簽名：信息m的簽名被定義為（4n+2）元組，即σ = （e1，e2，…，en;i0，v，m1，m2，…，mn;α1 β1，α2 β2，…，αn βn;），其中i0∈Z n。

環驗證算法（m，σ）：對于信息m的環簽名σ =（e1，e2，…，en;i0，v，m1，m2，…，mn;α1 β1，α2 β2，…，αn βn），驗證者可以按照如下步驟進行驗證：

1.驗證陷門置換[4]：驗證者首先驗證等式gmi=eαi

i? modp（i = 1，2，...，n）是否成立。如果等式成立，繼續下一步驗證，否則退出驗證。

2.驗證環等式：驗證者驗證等式：

v= h是否成立。若成立，驗證者認為環簽名有效，否則拒絕。

環簽名的可轉化性是基于離散對數知識的[5]，其中有l = logαs，l 是由真實的簽名者Bs在生成環簽名時隨機從Z *p選取的。由αs計算l是一個DLP（離散對數問題），這在數學上還沒有有效地解決方法。Ren-Harn在自己的方案中聲稱只有真實的簽名者才知道αs的離散對數l，因此他能夠向驗證者證實自己的身份，而其他的環成員都做不到。接下來，我們將呈現這一結論是的不成立性，所有的環成員都可以向驗證者宣布自己是真實的簽名者。

2.2? ?Ren-Harn方案的不足

在文獻[6]中，Ren-Harn聲稱自己的廣義環簽名是可轉化的，即他們認為他們的方案能夠通過可轉化環簽名定義中要求的環轉化和環轉化驗證兩大算法。但是王華群等人[6-7]對Ren-Harn方案提出了一種攻擊方法。通過密碼分析，我們看到Ren-Harn的環簽名并不能滿足可轉化性，因為環里的每個成員都有能力通過公布秘密信息來聲稱是自己生成的環簽名。這也就意味著Ren-Harn的方案失敗了。

如果Bi是真實的簽名者，即Bi = Bs，那么不用計算，他就能知道αs的離散對數l，因為l是他自己隨機選取的。因此他可以向驗證者證實自己的身份，從而實現了環簽名向普通簽名的轉化。

如果Bi不是真實的簽名者，他仍然可以宣布自己是真實的簽名者。因為他能夠通過gmi= eαi

i? eβi

i? modp得到mi = diαi + li βimod（p-1），進一步就可以計算li = （mi - diαi）β-1

i? mod（p-1）。這樣的話，任何非真實的簽名者也可以通過提供l來聲稱自己是真實的簽名者，攻擊方法成功。

從以上的密碼分析來看，Ren-Harn的方案是不安全的，即對于非真實簽名者的不可轉化性。

3? ?改進后的方案及安全性分析

3.1? ?改進后的方案

在這一部分，對Ren-Harn方案加以改進，引入時間戳變量t，即基于時間戳的Ren-Harn方案[7]，使其滿足可轉化性。

在改進的過程中，我們繼續沿用Ren-Harn方案中的一些概念。具體方案如下：

環簽名算法：（m，e1，e2，…，en，ds，s）：m為將要被簽名的信息，ds為簽名者Bs的私鑰，e1，e2，…，en為各個環成員的公鑰，簽名者按如下步驟計算環簽名：

1.計算信息摘要值：k = h（m）;

2.隨機選取膠值（初始化值）：簽名者Bs隨機選取初始化值v∈Zp。

3.為信息mi生成偽造簽名（αi，βi）：真實的消息簽名者任意選擇ai∈Zp-1，bi∈Z*p-1（其中i = 1，2，...，n，i≠s），那么簽名（αi，βi）可以從獲得gi（ai，bi） = （mi，αi，βi）獲得。

4.求解m：簽名者Bs隨機選取初始化值r∈Zp，計算t = h（e1‖e2‖…‖es - 1‖es + 1‖…‖en，r）。假設真實的簽名者所簽名信息的下標為is。令

v= h（m‖t，v），

v= h（m‖t，vm），

v= h（m‖t，vm），

v= h（m‖t，vm），

上面所有式子里面出現的下標都屬于Zn，有v= v。為了形成一個環，令vm = v，這樣可以得到m= vv。

5.利用簽名者的陷門信息對m簽名：真實的簽名者Bs隨機選擇x∈Z *p-1，計算l = h（x，es），要求gcd（l，p - 1） = 1，那么對m產生的簽名為（αi，βi） = （glmodp（m- diαi）l-1mod（p-1）。

6.輸出環簽名：信息m的簽名被定義為（4n+3）元組，即σ = （e1，e2，…，en;i0，v，m1，m2，…，mn;α1 β1，α2 β2，…，αn βn;t），其中i0∈Z n。

環驗證算法（m，σ）：對于信息m的環簽名σ =（e1，e2，…，en;i0，v，m1，m2，…，mn;α1 β1，α2 β2，…，αn βn;t），驗證者可以按照如下步驟進行驗證：

1.驗證陷門置換：驗證者首先驗證等式gmi= eαi

i

eβi

i? modp（i = 1，2，...，n）是否成立。如果等式成立，繼續下一步驗證，否則退出驗證。

2.驗證環等式：驗證者驗證等式：

v= h是否成立。若成立，驗證者認為環簽名有效，否則拒絕。

提出的基于時間戳的Ren-Harn方案是滿足可轉化性的，具體驗證過程如下：

環轉化算法：有些時候，真實的簽名者Bs需要向驗證者證明自己的身份。因此，他必須通過公布自己的秘密信息（r，x）來把無條件匿名的環簽名轉化為普通簽名。

1.驗證者首先驗證t = h（e1‖e2‖…‖es - 1‖es + 1‖…‖en，r）是否成立，若成立，驗證者可以通過比較e1，e2，…，es - 1，es + 1，…，en和e1，e2，…，en在es沒有參加運算的情況下來指出Bs是真實的簽名者。

2.因為x∈Z *p-1，l = h（x，es），gcd（l，p - 1） = 1，Bs

能夠通過秘密值x來證實自己是真實的簽名者。其他的環成員Bi（i≠s）即使能夠通過文獻[8]中的攻擊方法求得Ii，但由于哈希函數h的單向性，仍然無法獲得秘密值x。

環轉化驗證算法[8]：知道了秘密信息（r，x），驗證者可以按照以下步驟來驗證環簽名的有效性：

1.首先，驗證者驗證（e1，e2，…，es - 1，es + 1，…，en）∈σ = （e1，e2，…，en;i0，v，m1，m2，…，mn;α1 β1，α2 β2，…，αn βn;t），是否成立，若成立，則認為環簽名有效，否則拒絕。

2.然后，驗證者驗證t = h（e1‖e2‖…‖es - 1‖es + 1‖…‖en，r）和l = h（x，es）是否成立，若成立。則接受簽名，否則拒絕。

3.2? ?安全性分析

在Ren-Harn方案的基礎上，通過引入時間戳變量，使Ren-Harn方案得到改進，進而滿足可轉化性的定義，因此我們的方案是安全的。

如果Bi是真實的簽名者，即Bi = Bs，那么他可以通過公布自己的秘密信息（x，r）來實現從環簽名向普通簽名的轉化，也就證實了自己的身份。但是如果他不愿意透露秘密信息，任何人都無法知道是他產生了簽名。

如果Bi不是真實的簽名者，即Bi≠Bs，他不能證明自己是真實的簽名者。即使Bi知道了Bs的秘密信息（x，r），他會計算t′ =? h（e1‖e2‖…‖ei - 1‖

ei + 1‖…‖en，r）和l′ = h（x，ei），很明顯t′≠t，并且αi= gl′modp，αi[∈] σ = （e1，e2，…，en;i0，v，m1，m2，…，mn;α1 β1，α2 β2，…，αn βn;t），故非簽名者βi無法證實自己是真實的簽名者。

經過以上分析，看到新方案滿足對于可轉化的環簽名的三點安全要求。由于該方案是基于Ren-Harn方案進行改進的，因此改進后的方案同樣滿足該定理[9]：基于ElGamal簽名方案的廣義環簽名對于隨機預言模型（ROM）中的適應性選擇消息攻擊是安全的。

4? ?結? ?論

廣義環簽名是一種時新的并且非常實用的簽名。文中主要針對Ren-Harn方案的不足進行了改進。經過驗證，基于時間戳的Ren-Harn方案是可轉化性的，也就是說新方案能夠保障真實的簽名者對于環簽名的獨創性，它嚴格拒絕任何非簽名者來對環簽名進行轉化。

參考文獻

[1]? ?BENDER A，KATZ J，MORSELLI R，et al.Ring signatures：stronger definitions，and constructions without random oracles[J]. Journal of Cryptology，2008，30（9）：114-138.

[2]? ?BOYEN X.Mesh signatures：how to leak a secret with unwitting and unwilling participants，Proceedings of the 26th International Conference on the Theory and Applications of Cryptographic Techniques[J]. Cryptology-Eurocrypt，2007，2013，13（2）： 210-217.

[3]? ?LEE K，WEN H，HANG T，et al. Convertible ring signature[J].IEEE Proceedings Communications，2003，19（4）： 251-260.

[4]? ?WANG C，LIU Y.A new ring signature scheme with signer-admission property[J]. Information Sciences，2007，78（6）： 747-754.

[5]? ?REN J，HARN L.Generalized ring signatures，IEEE Transactions on Dependable[J]. Secure Computing，2008，85（8）： 155-163.

[6]? ?RIVEST L，SHAMIR A，TAUMAN Y，et al.How to leak a secret，Proceedings of the 7th International Conference on the Theory and Application of Cryptology and Information Security[C]. Advances in Cryptology-Asiacrypt，2011，15（6）：552-565.

[7]? ?WANG H，ZHANG F，SUN Y，et al. Cryptanalysis of a generalized ring signature scheme，IEEE Transactions on Dependable[J]. Secure Computing，2009，26（2）：149-151.

[8]? ?ELGAMAL A.A public-key cryptosystem and a signature scheme based on discrete logarithms[J]. IEEE Transactions on Information Theory，2015，80（12）：469-472.

[9]? ?GOLDWASSER S，MICALI S，RIVEST L，et al. A digital signature scheme secure against adaptive chosen-message attacks[C].SIAM Journal on Computing Special Issue on Cryptography，2017，90（12）：125-140.