基于混沌蝙蝠算法的無人機控制系統故障診斷優化

王 旭 路 凱 肖玲斐

1(許昌電氣職業學院 河南 許昌 461000) 2(許昌學院 河南 許昌 461000) 3(南京航空航天大學能源與動力學院 江蘇 南京 210016)

0 引 言

目前，由于網絡技術的快速發展，分布式控制系統在大型無人機發動機控制系統上的應用也越來越受人關注[1-2]。分布式控制系統實質上是一種網絡控制系統，它與傳統的點對點控制系統相比最大的不同在于其相關數據是通過總線進行傳輸的，這會造成誘導時延以及數據丟包等問題，故在進行故障診斷時必須將總線帶來的不利因素考慮進去。王越男[3]設計了一種針對離散時滯系統的魯棒故障檢測觀測器，使得檢測殘差能夠對噪聲信號具有較好的魯棒性能。文獻[4-6]均利用H∞理論針對不確定系統、時延網絡控制系統、非線性系統進行魯棒故障檢測，使得系統在強噪聲條件下依舊能夠保證良好的故障檢測性能。但是上述文獻均只考慮如何提高檢測系統對噪聲干擾信號的魯棒性，未考慮對故障信號的影響。

為提升檢測系統對噪聲信號的魯棒性以及故障信號的敏感性，本文針對雙通道多包傳輸的短時變時延無人機發動機網絡控制系統，提出一種基于改進蝙蝠的故障檢測觀測器優化設計方法。首先對原系統建立故障觀測器，將雙通道多包傳輸轉換為切換系統，將短時變時延建模為一種系統不確定性。然后將殘差信號對噪聲信號和故障信號的傳遞函數比值作為適應度函數，使其對故障信號敏感，對噪聲魯棒，利用改進蝙蝠算法在保證觀測器殘差系統穩定的條件下使得目標函數最小，從而求得最優故障觀測器增益矩陣。

1 系統建模

首先建立短時變時延無人機發動機網絡控制系統，進行如下合理假設：

(1)傳感器節點為時間驅動，而控制器與執行機構節點均為事件驅動，采樣周期為常數T。(2)傳感器到控制器與控制器到執行機構之間均存在網絡誘導時延，分別為τsc和τca，且滿足τsc+τca≤T，由于計算時延很小，故忽略不計。(3)傳感器到控制器與控制器到執行機構之間均為多包傳輸，且采用靜態調度的方式。(4)存在未知擾動，但不考慮數據丟包以及數據包時序錯亂。

已知該系統的離散時間模型為：

(1)

進一步建立觀測器誤差模型。考慮系統的雙通道多包傳輸，假設從傳感器傳輸到控制器的狀態量x(k)被封裝在m個數據包中，從控制器傳輸到執行機構的控制量u′(k)被封裝在n個數據包中，令控制器與執行機構收到的狀態量與控制量分別為x′(k)與u(k)。

(2)

故

(3)

同理，控制量的各個數據包之間有如下關系：

(4)

即

(5)

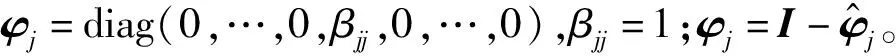
狀態反饋控制器為：

(6)

式中：K為狀態反饋控制器增益矩陣。將式(6)與式(5)和式(1)聯立然后定義增廣向量z(k)=[xT(k)x′T(k-1)uT(k-1)]T，可以得到等價模型：

(7)

2 改進BA設計

蝙蝠算法一經提出，就由于其簡單性與有效性得到了廣泛的關注[8-10]。具體的蝙蝠算法迭代過程為：蝙蝠的坐標為一個解，該坐標包含速度和適應度函數值，蝙蝠種群利用新發出的頻率、脈沖發射速率和聲波響度得到新的解集，然后依次進行迭代得到最優值[11-12]。數學表達式如下：

Fi=Fmin+(Fmax-Fmin)×RNRN∈[0,1]

(8)

(9)

(10)

為提升算法的便利性，給出相應的更新公式如下：

Xnew=Xbest+α×Al

(11)

式中：α代表在[-1,1]區間內的隨機數;Al表示第l代蝙蝠聲波響度的平均值。

在式(11)的基礎上，每一只蝙蝠的脈沖發射率Ri以及相應的脈沖聲波響度Ai也會進行更新，具體的更新過程如下：

(12)

(13)

式中：β、ω為常數，β>0，0<ω<1。

BA具有收斂性強以及搜索范圍大的優點，但是蝙蝠位置的更新效果過分依靠速度參數，使得在優化過程后期，容易陷入局部極值[13-14]。為提升其優化精度，將遺傳算法中的理論與基本BA結合，具體步驟如下：

Step1將交叉比例和交叉方法引入蝙蝠種群的更新過程，具體的過程如下：

(14)

Step2為使得更新后的種群xi(t+1)發生變異，設置相應的變異激活函數如下：

(15)

式中:α∈[0.5,0.6]；β∈[0.1,0.3]；k代表種群內第k只蝙蝠；n代表維度；N代表蝙蝠種群的總個數；rand是[0,1]的隨機數。若滿足Activate(k)<1，則使得蝙蝠發生變異。

Step3變異主要包括均勻變換以及高斯變換，均勻變換主要為了提升收斂速度，高斯變換主要提升跳出局部極值的能力，相應的均勻變換和高斯變換如下：

(16)

式中：σ代表高斯分布的標準差；Lmax表示最大臨界值；μ表示更新參數；x*表示目標位置。

在BA中，已知脈沖發射率更新迭代的初始值選則具有一定的主觀性，因此該參數選擇可能使得算法具有一定的人為保守性而無法達到最優。因此進一步改進脈沖發射率的迭代過程:

(17)

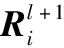
圖1 混沌BA脈沖發射率

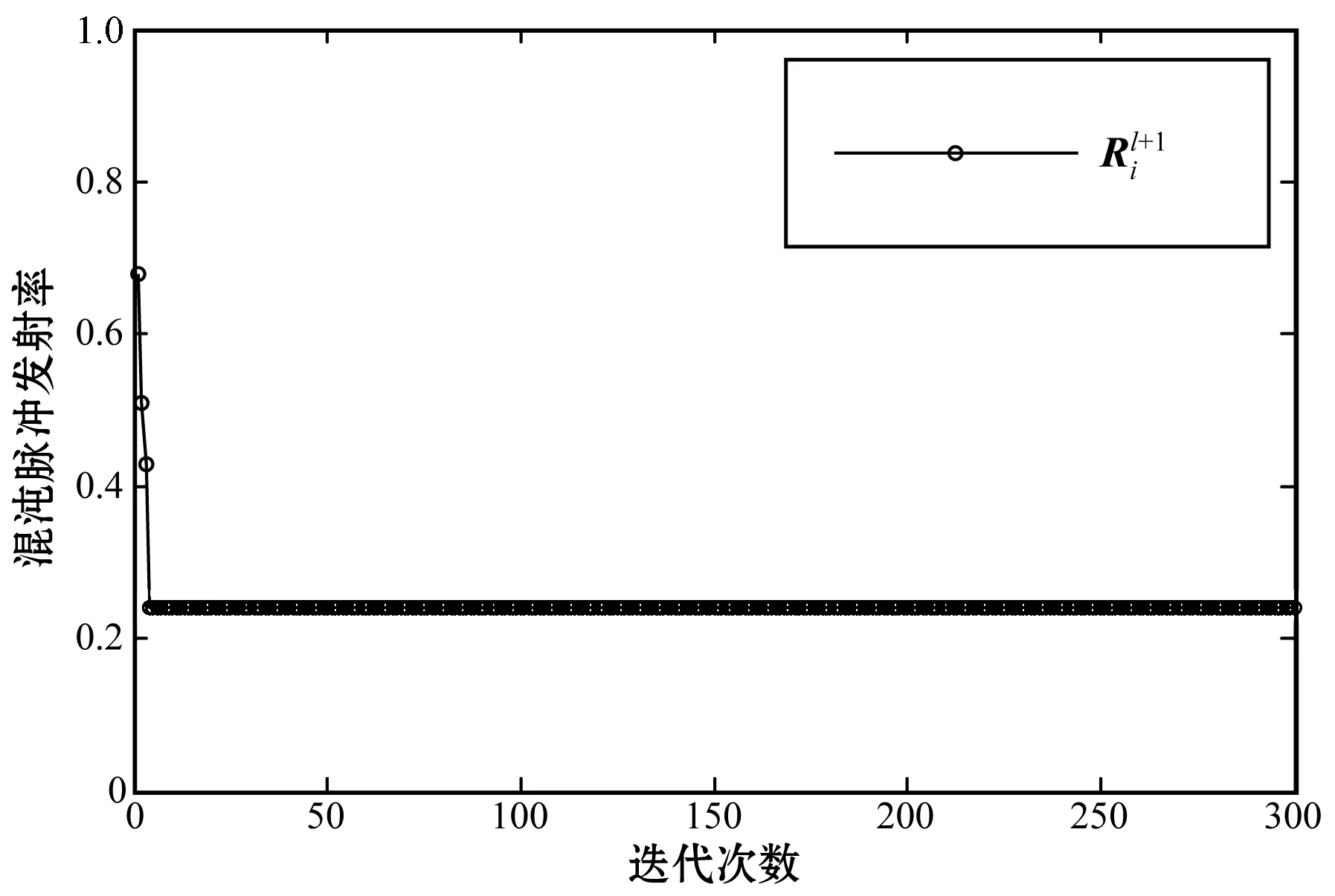
圖2 基本BA脈沖發射率

3 改進BA的故障檢測觀測器設計

設閉環觀測器為：

(18)

式中：Ll(l=1,2,…,m×n)是需要求的觀測器增益矩陣。觀測器結構如圖3所示。

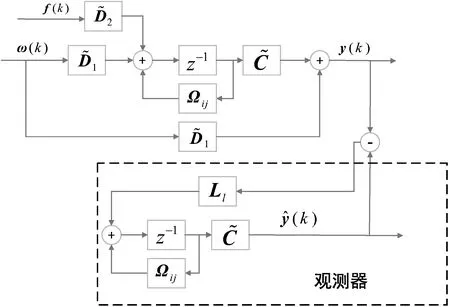
圖3 觀測器結構

(19)

對式(19)進行Z變換，則殘差信號ε分別到擾動信號ω和故障信號f的傳遞函數矩陣為：

(20)

本節利用改進BA對故障檢測觀測器的增益矩陣Ll進行優化必須遵循下列幾點要求：

(1)穩定性。在系統擾動為0時，殘差信號能夠收斂。

(2)靈敏性。殘差信號對故障信號要相當敏感，即殘差對故障的增益要大。

(3)魯棒性。殘差信號對擾動信號的魯棒性要強，即殘差對擾動的增益小。

首先必須要滿足穩定性要求，這是實現故障檢測的基礎。由文獻[3]可得到穩定性的條件為：

(21)

由于Ωij中含有不確定矩陣F(τk)，所以進行如下變換：

(22)

將式(22)代入式(21)，根據文獻[6]可知該式等價于存在ηl>0(l=1,2,…,m×n)，使得：

(23)

式中：*表示對稱矩陣。

運用ArcGIS 10.2進行高低聚類分析，得出如圖1所示商品住宅價格高低聚類圖。從圖中可以看出中山區、西崗區和沙河口區的大部分住宅價格以高高聚集為主，甘井子區住宅價格主要為低低集聚為主。高低聚集區主要分布在中山區北部和西崗區一小部分住宅。

(24)

保證穩定性的條件：所取的故障觀測器增益矩陣Ll必須滿足存在對稱正定矩陣P以及ηl>0(l=1,2,…,m×n)，使得式(24)成立。

為了增強誤差觀測器的魯棒性與靈敏性，設適應度函數為:

(25)

式中：J1為誤差系統對噪聲在整個噪聲頻率中的傳遞函數增益，為了減小噪聲對系統的影響，J1要盡量的小；ωr為噪聲信號的頻率點；J2為誤差系統對故障在整個故障信號頻率中的傳遞函數增益，由于傳感器或者執行機構故障信號大多集中在低頻段[15],故令傳遞函數變量z=1。為了增大系統對故障信號的敏感性，故必須使得J2盡可能大，所以優化的目標為求取適應度函數fitness的最大值。

綜上所述，基于改進BA的故障檢測問題可以歸結為以下優化問題：

minfitness

(26)

具體的優化步驟為：

Step1設置算法的基本參數與初始值大小，給定輸入為觀測器矩陣的元素，并計算出初始適應度函數值。

Step2對蝙蝠種群進行交叉運算，判斷蝙蝠個體是否發生變異，若發生變異，則按照變異過程進行處理。

Step3更新此時的蝙蝠種群位置，將此時的位置代入式(26)中的線性矩陣不等式，若存在可行解，則更新后的種群以細微擾動量在當前最優解附近重新尋優，否則重新進行位置尋找。

Step4計算蝙蝠種群新位置的適應度函數值，并更新聲波響度、混沌脈沖發射率以及最優值。

Step5對比得到當前種群內適應度函數的最優值，并記錄最優值的位置。

Step6判斷是否達到最大迭代次數Iterate_times，若滿足，則停止算法并輸出適應度函數的極值以及對應的最優位置，即最優的故障觀測器增益矩陣Ll的各個元素，否則返回Step 2，再進行下一次迭代尋優。

4 仿真算例及結果分析

4.1 控制系統半物理仿真平臺

本文的仿真驗證借助航空發動機分布式控制系統半物理仿真平臺來進行，系統結構如圖4所示。由發動機模擬計算機、控制計算機、智能執行機構、智能傳感器以及CAN總線五部分組成。發動機模擬計算機運行發動機數學模型，智能傳感器通過接收模型計算機中解算出的各個傳感器模擬量，進行數據轉換，并通過串口上傳至CAN總線，與發動機控制計算機進行實時通信。控制計算機中接收CAN總線上的數字量，運行控制算法，輸出控制信號至CAN總線，控制面板中實時顯示發動機運行數據和曲線，并能夠在控制面板中進行控制器參數調整、故障模擬、通信檢測等操作。智能執行機構從CAN總線中接收控制信號，以模擬量信號輸出至發動機模擬計算機中進行發動機轉速控制。具體的實物如圖5所示。

圖4 系統半物理平臺結構

圖5 分布式控制系統仿真平臺實物

4.2 基于半物理平臺的仿真

設無人機發動機的狀態方程為：

(27)

以T=20 ms為采樣周期離散化可得:

(28)

(29)

在求解過程中，設置尋優解空間為[-10,10]6，采樣步長為τ=20 ms，最大迭代次數gmax=1 000，種群規模sizepop=100，協同子種群m=5,α0=β0=0.7。

分別以基本BA和改進BA對故障觀測器增益矩陣Ll(l=1,2,3,4)進行優化，其中L1的優化結果如圖6和表1所示。

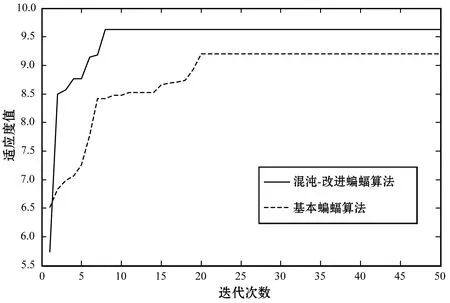
圖6 優化結果對比圖

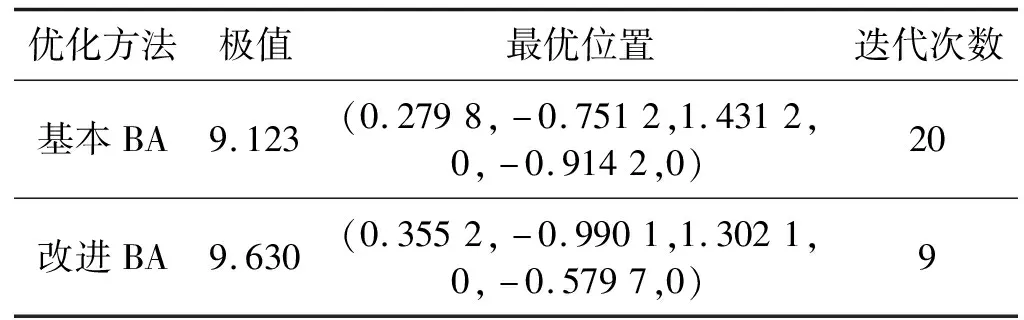
表1 優化結果數據對比表

從圖6和表1中可以看出，改進的BA的極值較小，且收斂時間比基本BA少了9個迭代周期；改進的BA收斂曲線更加平滑，說明該方法更容易跳出局部極值，對在故障觀測器矩陣優化上相對于基本BA在收斂速度、收斂性能以及收斂精度上具有較大的提高，驗證了改進BA的優越性。

從表1中可以得到最優適應度函數所對應的故障觀測器矩陣為L1=[0.355 2 -0.990 1 1.302 1 0-0.579 7 0]T,同理可得其他三種情況的觀測器增益矩陣為：

為在半物理平臺上模擬出雙通道多包傳輸，由于系統傳輸數據量較小，數據包的數據區只需要三位，故將CAN總線中傳輸數據包的第四個數據位設置為數據包標志位。設置的數據包隨機傳輸序列如圖7所示。

圖7 數據包隨機傳輸序列

系統控制器根據傳輸的數據包來自動切換故障觀測器增益矩陣，從而實現對整個系統的故障檢測。為模擬系統的傳感器短路故障，對系統施加一個幅值較小的階躍型故障，同時添加一個幅值為0.8的噪聲信號，檢測結果如圖8和圖9所示，分別代表傳統魯棒故障觀測器[3]與改進BA優化的故障觀測器檢測殘差結果。可以看出傳統方法的殘差信號振動幅值為0.1，而優化方法的殘差振動幅值僅為0.075，這說明噪聲信號對傳統檢測方法的影響較大。另外，傳統檢測方法的殘差與正常狀態無法完全通過設定閾值來區分，而圖8顯示的優化故障觀測器方法對故障信號有明顯的放大作用，且噪聲分量明顯減少，閾值設定范圍從傳統的0.100到0.155擴展為0.075到0.193，范圍擴大2.14倍，說明該方法更有利于區分故障狀態與正常狀態。

圖8 傳統魯棒觀測器檢測殘差

令傳感器漂移模擬故障為f=0.15×(t-20)×δ(t-20)，給定幅值為0.05噪聲信號，圖10分別為利用文獻[3]的故障觀測器方法與改進BA優化方法所得到的殘差變化對比圖。可以看出傳統的故障觀測器方法噪聲較大，而優化的故障觀測器方法噪聲分量明顯減少，故障信號有明顯的放大作用，殘差能夠更快地增大到閾值，從而更快速地檢測出系統的漂移故障。

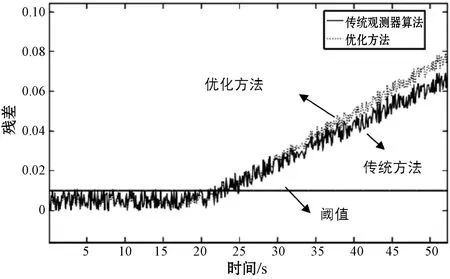
圖10 斜坡故障監測殘差對比

進一步給定一個傳感器的非線性故障：

(30)

此時同樣給定一個幅值為0.05的噪聲信號,檢測殘差對比結果如圖11所示。可以看出，傳統方法的殘差振動約為0.003 8，而優化方法的殘差幅值為0.001 8，這說明噪聲信號對傳統檢測方法影響更大。另外，傳統方法的閾值選擇范圍為0.003 8到0.012 0，而優化方法的閾值選擇范圍為0.001 8到0.021 0，范圍增大2.34倍，進一步說明該優化方法對故障狀態與正常狀態具有更好的區分度。

圖11 非線性故障檢測殘差對比圖

綜上所述，利用改進BA優化的觀測器增益矩陣能夠使得殘差信號放大故障信號而減弱噪聲的影響，有效地減少故障的漏報率，提升故障預警的準確性。

5 結 語

為了更加貼近實際的UAV網絡控制系統，考慮雙通道多包傳輸的短時變時延UAV發動機網絡控制系統，利用改進BA對同時兼具故障敏感性與噪聲魯棒性的適應度函數進行優化，從而得到最優觀測器增益矩陣。本文的研究結果表明：

(1)該觀測器能夠保證切換條件下的殘差漸進穩定。

(2)改進BA在保證一定收斂速度的條件下，相對于基本BA而言具有更好的收斂精度。

(3)提出的傳感器故障檢測優化方法不僅能夠抑制噪聲信號對殘差幅值的影響，還能夠有效提升故障狀態與正常狀態的區分度，進一步擴大閾值的選擇范圍，有效地提升傳感器各類故障的檢測率，減少誤報率，并且能夠增大人工設定閾值的容錯率，進一步說明該方法的有效性。