兩輪移動巡檢機器人的區間二型模糊滑模控制

陳 瑤 毛雅潔 趙 濤 劉佳豪

(四川大學 四川 成都 610065)

0 引 言

1986年，日本的Kazuo Yamafuji教授制作了最早的自動站立式兩輪機器人[1]；2001年，美國發明家迪恩·卡曼發明了電動代步工具Segway[2],該機器人采用了模糊控制方法，可通過控制車體上方的方向傳感器實現機器人的轉彎，為代步兩輪自平衡機器人在生活中的應用打下基礎；2002年，丹麥Lego公司的Steve設計出一款玩具型兩輪自平衡機器人LegWay[1],采用光電接近探測器實現機器人的平衡控制，并在此前提下，實現軌跡跟蹤；同年，瑞士的研究人員研制出一臺借助陀螺儀和加速度計來采集傾角信息的兩輪移動機器人，可以實現U形和零半徑回轉[1]；2008年，美、日公司合作推出了可播放音樂還可以在跟蹤模式下追隨人運動的AMP(Automatic musical personality)兩輪機器人；美國學者David P.Anderson教授獨立設計的兩輪機器人nBot[14]采用模糊控制方法，能夠使兩輪機器人保持平衡。

國內的科學家也在積極研究兩輪移動機器人，并取得了一些成果。中國科學研究院自動化所研發并研制CASIA-I智能移動機器人通過多傳感器信息融合技術，可以實現語音會話功能[1]。2003年，中國科學技術大學研制出一種兩輪代步電動車，采用了三維動力學的倒立擺控制原理[3]，可使機器人在多種運行狀態下保持平穩，如前進、后退、轉彎和剎車。2005年，哈爾濱工程大學尹亮制作了由上位機和車體共同構成的自平衡機器人Sway[3]，采用的雙軸加速度傳感器和紅外傳感器能夠提高檢測精度，可靠的數據采集和獨特的算法有助于機器人平穩運行。

以兩輪移動巡檢機器人為對象，主要進行自平衡控制和軌跡跟蹤控制。目前，根據機器人模型的線性化和非線性化，控制方法也分為線性控制、非線性控制和智能控制。傳統的線性控制方法有PID算法、LQR算法[1，4]以及極點配置法等，一般都基于狀態反饋，其設計簡便，相對容易實現。然而由于兩輪移動巡檢機器人本身是具有非線性及強耦合等多種特性的系統，線性化的處理必然會產生系統的抗干擾能力下降、控制范圍縮小以及控制效果不佳等問題[1]。非線性控制或智能控制[1]主要有backstepping控制[5]、滑模變結構控制[6]、模糊控制[7]、神經網絡控制[8]等。與傳統線性控制相反，其設計復雜，在物理上往往難以實現，但能夠有效地增加控制范圍且魯棒性更好，控制效果更優。

模糊控制是以模糊集合論、模糊語言變量和模糊推理為基礎的一種計算機數字控制技術[9]。模糊控制的控制精度不高，適合系統數學模型不精確的非線性系統的控制[1]。自從Zedeh教授創立模糊數學以來[10]，模糊控制器逐漸走入實際生產中，并且解決了很多實際問題。隨著社會的發展，T-S模糊控制出現，相較于傳統的模糊控制器，其在處理非線性系統穩定性分析及控制器綜合方面發揮著巨大的作用。一型T-S模糊控制在一型模糊控制的基礎上展開，可以表示光滑非線性系統，許多學者對此進行拓展和優化，使其具有更強的非線性能力。但隨著系統的復雜性和不確定性的增加，用一個確定的隸屬函數值描述某個對象屬于某個模糊集的程度愈加困難，面對此種情況，Zedeh教授提出二型模糊集的概念[11]，以提高系統應對復雜性及不確定性的能力。二型模糊集的隸屬度表現為一型模糊集而不是確定的函數值，因此，在高度不確定場合下，二型模糊集具有更佳的控制性能[10]。為了簡化計算，在二型模糊控制器的基礎上，學者們提出區間二型T-S模糊控制器[11]。

滑模變結構控制是一類特殊的非線性控制。滑模控制方法的系統“結構”并不是固定的，它會依據當前的狀態不停地切換控制量，使系統沿著提前設計好的“滑動模態”的狀態軌跡運動，也就是說滑模控制本質的特點表現為控制的不連續性[4]。滑動模態與控制對象的參數以及各項擾動無關，且可以根據實際需要進行設計，故滑模控制具有魯棒性強、反應快速、算法簡單、方便物理上實現等多個優點。然而，由于系統中存在切換函數，狀態軌跡到達滑模面后，會在滑模面上下來回穿越，從而產生抖振[12]。滑模控制可以很好地提高兩輪移動巡檢機器人的魯棒抗擾性能，克服其數學模型不確定的缺點[13]，但同時也會因為抖振大大增加執行機構的機械磨損。為了改善終端滑模控制帶來的抖振現象，有學者提出了設計基于趨近律滑模控制方法[14]。

兩輪移動巡檢機器人具有轉向靈活的特點，在一些狹窄的空間場合里也能夠高效地完成任務，所以對兩輪移動機器人的研究非常具有現實意義。但是兩輪移動巡檢機器人的系統特性使得單一控制方法無法完全兼顧各方面的性能。針對該問題，本文提出將模糊控制與滑模變結構控制合理地結合在一起，優勢互補，從而消除滑模控制的帶來抖振現象，以便更好地控制兩輪移動巡檢機器人。本文將先采用終端滑模控制控制機器人，再設計區間二型模糊滑模控制器，最后通過MATLAB來驗證所提出方法的有效性。

1 兩輪移動巡檢機器人數學模型

建立數學模型的主要參數及具體含義見表1。HL、HR、HTL、HTR、VL、VR、VTL、VTR為機器人不同結構之間的相互作用力，具體含義可參考文獻[1]。

機器人的非線性動力學模型建立如下[15]：

(1)

系統中各符號表達式如下：

f=[f1f2f3]T

(2)

(3)

u=[CθCδ]T

(4)

d=[d1d2d3]T

(5)

具體表達式如下：

(6)

(7)

f3=0

(8)

(9)

g12=0

(10)

(11)

g22=0

(12)

g31=0

(13)

(14)

(15)

(16)

d3=0

(17)

將表1中的參數代入式(1)的非線性動力學模型中，可以得到完善的機器人模型。

2 兩輪移動巡檢機器人的終端滑模律

根據終端滑模控制的基本原理，針對兩輪移動巡檢機器人中位移傾角子系統和偏航角子系統的非線性數學模型，詳細介紹終端滑模器的設計過程。

兩輪移動巡檢機器人的系統動力學模型可表示為[1，15]：

(18)

本節所進行的設計不考慮外部擾動d(t)。系統可改寫為：

(19)

定義機器人的軌跡跟蹤誤差，xrr、θr、δr分別代表xr、θ、δ的期望值：

(20)

對式(20)微分，得到：

(21)

對于位移傾角子系統，根據終端滑模的特性，設計滑模面為：

(22)

式中:c1>0,c2>0,c3>0,p、q、m、n是奇數，且p>q>0,m>n>0。

(23)

選擇指數趨近律:

(24)

式中：ε1>0,k1>0。

根據式(23)和式(24)，得到位移傾角子系統控制律為：

(25)

式中:ε1>0,k1>0。

對于偏航子系統，設計滑模面：

(26)

式中:c4>0,u、v是奇數，且u>v>0。

對式(26)作微分，可以得到：

(27)

選取指數趨近律：

(28)

式中：ε2>0,k2>0。

根據式(27)和式(28),得到偏航子系統控制律為：

(29)

式中:ε2>0,k2>0。

根據滑模可達性條件，選取李雅普諾夫函數:

(30)

對式(30)進行微分：

s2(-ε2sgn(s2)-k2s2)=

(31)

由上可知符合設計要求，兩輪移動機器人系統能夠在設計的滑模控制律的控制作用下，實現對參考位移和參考角度的軌跡跟蹤。

3 區間二型模糊滑模控制

為了進一步提升控制性能，在終端滑模控制的基礎上，利用區間二型模糊控制器消除滑模控制帶來的抖振現象，即式(24)和式(28)中的k1和k2由區間二型模糊控制器產生，通過對這兩個參數在線動態調整，使趨近律更加合理，并消除由滑模控制產生的抖振現象。模糊控制器有兩種類型：一種是T-S模糊類型；另一種是Mamdani類型，本文采用后者，具體步驟如下：

1)確定區間二型模糊控制器的結構，選擇輸入、輸出變量。

2)選擇覆蓋模糊論域的區間二型模糊子集，確立隸屬函數。

(1)位移傾角子系統：

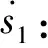
s1

(2)偏航角子系統：

s2

3)區間二型模糊規則的建立。設計的區間二型模糊控制規則如表2所示。其中，模糊隸屬函數根據所處位置分別命名為NB(負大)、NM(負中)、NS(負小)、ZE(零)、PS(正小)、PM(正中)、PB(正大)。

表2 區間二型模糊規則表

4)將所設計的區間二型模糊滑模控制器應用于兩輪移動巡檢機器人，并與一型模糊滑模控制器和純終端滑模控制器進行比較，驗證其有效性及優越性。

4 仿真分析

在MATLAB平臺上對所設計的區間二型模糊滑模控制器進行仿真，用模糊控制器調整滑模控制律中切換控制項的增益，即模糊控制在滑模控制的基礎上進行控制，參考信號為滑模控制參考軌跡。

本節分為兩部分對系統仿真結果進行闡述：一是位移傾角子系統；二是偏航角子系統。通過對這兩個子系統的仿真，可以得出結論：區間二型模糊滑模控制不僅能使系統輸出達到指定位置，還能消除滑模控制帶來的抖振，證明了本文方法在控制兩輪移動巡檢機器人上的有效性。

4.1 位移傾角子系統

仿真結果如圖3-圖8所示。其中：圖3是控制量位移x的變化曲線；圖4為傾角θ的變化曲線；圖5是控制律即輸入偏傾角轉矩Cθ的變化曲線；圖6是滑模面s1的變化曲線；圖7和圖8分別是位移和傾角跟蹤誤差曲線。

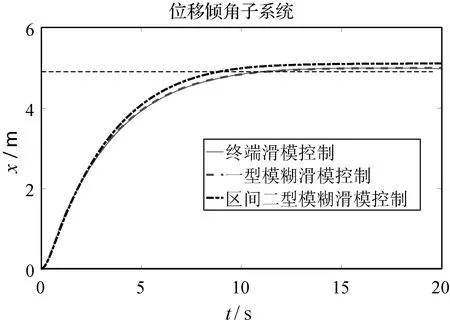
圖3 直線軌跡位移曲線

圖4 直線軌跡傾角曲線

圖5 輸入控制律(傾角轉矩)變化曲線

圖6 滑模面變化曲線

圖7 直線軌跡偏位移跟蹤誤差曲線

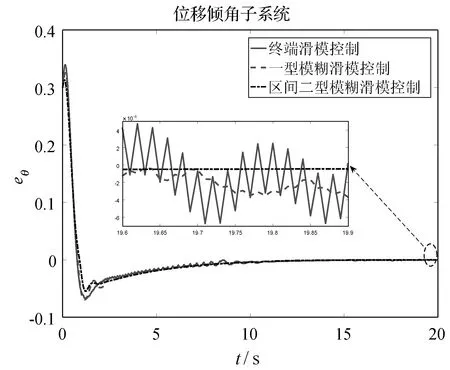
圖8 直線軌跡傾角跟蹤誤差曲線

根據圖3和圖4，在三種不同控制器控制下，位移和傾角均跟蹤上了參考軌跡。對位移曲線來說，加入一型模糊控制器后，曲線沒有明顯變化，加入區間二型模糊控制器后，調節時間加快。對傾角曲線來說，加入模糊控制后，系統超調明顯降低，抖振減小，其中區間二型模糊滑模的控制效果比一型模糊更好，在局部放大圖中，區間二型模糊控制下的曲線幾乎是一條直線。

根據圖5，不同控制方法下輸入傾角轉矩的變化范圍不同，變化范圍由大到小依次為終端滑模控制、一型模糊滑模控制、區間二型模糊滑模控制。所設計的模糊控制能夠動態地調整控制律中切換項的增益。

根據圖6，不同控制方法下滑模面的變化不同，純滑模控制下，滑模面在0附近密集變化，且范圍很大；一型模糊滑模控制下，滑模面變化范圍減小，且仍在0附近密集變化；區間二型模糊滑模控制下，變化范圍幾乎為一條直線，但值得注意的是，該滑模面不在0附近上下變動，而是略高于0點線。

根據圖7和圖8，位移誤差和傾角誤差均在較短時間內到達0附近。對位移誤差來說，純終端滑模控制和一型模糊滑模控制的穩態誤差幾乎一致，曲線重合，而區間二型模糊滑模控制的穩態誤差較前兩者來說稍大一些，但也在容許范圍之內。對傾角誤差來說，從整體圖來看，三種控制方法的穩態部分曲線重合，穩態誤差一致，從放大圖來看，在三種控制方法下，區間二型模糊滑模控制由于消除了由滑模控制產生的抖振，穩態誤差控制得最好。

4.2 偏航角子系統

仿真結果如圖9-圖11所示。其中：圖9是偏航角δ的變化曲線；圖10是控制律即輸入偏航角轉矩的變化曲線；圖11是滑模面的變化曲線；圖12是偏航角誤差跟蹤曲線。

圖11 滑模面變化曲線

圖12 直線軌跡偏航角誤差跟蹤曲線

根據圖9，在三種控制器的控制下，偏航角均跟蹤上了指定軌跡，且加入模糊控制器后，調節速度與調節時間基本沒有變化。比較抖振情況，根據局部放大圖，純滑模控制下，抖振范圍較大，約為3×10-3；一型模糊滑模控制下，變化范圍相較于滑模控制，有了很大的改善，約為2×10-4；區間二型模糊滑模控制下，即使在局部放大后，依然看不出任何波動，且相比一型模糊滑模控制，效果更好。

根據圖10，不同控制方法下輸入偏航角轉矩的變化范圍不同，純滑模控制下，變化范圍為-5～5；一型模糊滑模控制下，變化范圍為-0.316 2～0.316 2；區間二型模糊滑模控制下，變化范圍-0.006 7～0.006 7，肉眼范圍內，幾乎為一條直線，因此，模糊控制對切換項的增益起到了良好的控制效果。

根據圖11，不同控制方法下滑模面的變化不同，純滑模控制下，滑模在0附近變化較大，變化范圍在-0.2～0.4之間；一型模糊滑模控制下，滑模面在0～0.05內變化；區間二型模糊滑模控制下，變化范圍幾乎為一條直線。

根據圖12，三種控制方法均使偏航角的誤差在較短時間內到達0附近，模糊控制對該系統的穩態誤差有很大的改善。其中：純滑模控制下，穩態誤差約為5×10-3；一型模糊滑模控制下，穩態誤差約為8×10-4；區間二型模糊滑模控制下，穩態誤差為0。

5 結 語

本文針對兩輪移動巡檢機器人提出了區間二型模糊滑模控制器。通過區間二型模糊控制器對終端滑模控制律的切換項增益進行動態調整，以到達削弱甚至消除滑模控制帶來的抖振現象的目的。通過在仿真平臺上對終端滑模控制、一型模糊滑模控制以及區間二型模糊滑模控制仿真分析，所設計的區間二型模糊控制器在快速使機器人保持平衡的同時，能夠追蹤參考軌跡。此外，一型模糊滑模控制器能夠很好地削弱由滑模控制帶來的抖振，而區間二型模糊控制器能夠有效地消除由滑模控制帶來的抖振。本文所設計的區間二型模糊滑模控制器達到了預期的控制目的。