基于NMPC-PID的大型風電機組獨立變槳距載荷控制

曹松青 郝萬君

(蘇州科技大學電子與信息工程學院 江蘇 蘇州 215009)

0 引 言

隨著風電機組向著大型化方向不斷發展，風輪直徑和掃掠面積不斷增大，機組的疲勞載荷也相應增加，除了基本的功率控制需求，載荷控制也逐漸成為機組控制的重要組成部分[1-3]。由于獨立變槳距控制可以有效解決槳葉和塔架等部件的載荷在時間和空間上的不均勻問題，因此可以用獨立變槳調節來減小葉根揮舞彎矩，實現載荷控制[4-5]。

在獨立變槳距控制方面，近年來國內外學者進行了大量研究。文獻[4,6]提出了基于前饋-反饋結構的LQG獨立變槳距控制，可以很好地減小不平衡載荷。文獻[7]引入了帶增益調度的統一變槳距控制，在此基礎上附加基于LQR的獨立變槳距控制，在穩定輸出功率的同時有效降低了零部件的疲勞載荷。然而，LQG/LQR方法的優化是離線方式，難以顧及不確定性的影響，從而難以保證全局最優。文獻[8-9]分別提出基于徑向基函數(RBF)神經網絡PID的獨立變槳控制和基于神經網絡模型的預測自適應PID控制策略，雖然能分別降低俯仰載荷和偏航載荷，但忽略了d軸載荷控制和q軸載荷控制之間的耦合關系。文獻[10]將線性模型預測控制用于對風電機組的獨立變槳距控制，在一定程度上減小了風機載荷，但未考慮工況點偏移、模型失配和外界不可測干擾等影響。文獻[11]提出了基于非線性模型預測控制的獨立變槳控制，但其研究對象是海上浮動風電機組，而本文的研究針對陸上風電機組。

為了有效減小輪轂中心的俯仰力矩和偏航力矩，本文提出了基于NMPC-PID的大型風電機組獨立變槳距載荷控制策略。利用RBF神經網絡對風電機組模型進行在線辨識和校正，在預測模型中對風電機組的輸出進行預測，并將風速作為可測量擾動在預測模型中加以考慮。為進一步減小外部不確定性擾動的影響，在俯仰力矩和偏航力矩的控制通道上分別添加一個PID控制器進行反饋補償。

1 風電機組模型

大型風電機組的空氣動力學特性呈強非線性[12]。為了簡化分析，將槳葉視為剛性葉片，并對氣動載荷非線性模型在穩態工作點附近進行線性化，可得線性周期時變模型[13]。利用Coleman變換(又稱Park變換)，可實現風輪旋轉坐標系與輪轂固定坐標系之間的變量變換，從而可將周期時變模型轉換為線性定常模型[4,14]：

(1)

(2)

(3)

(4)

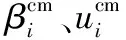
式中：Mzi、Fxi分別為第i個葉片根部揮舞方向上的力矩和力，Mxi、Fzi分別為第i個葉片根部擺振方向上的力矩和力，βi為第i個葉片的槳距角，vfli為葉片揮舞方向的相對有效風速，可以表示為[12]：

(5)

式中：ui為第i片槳葉上的等效風速，ψi為第i片槳葉的方位角。假定第一片槳葉的方位角為ψ，則有：

(6)

y=Cx+Dβu+Duv

(7)

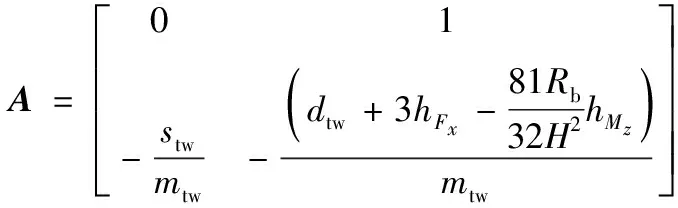
2 控制器設計

由上節內容可知，hMz、kMz、hFx、kFx、hMx、kMx為風電系統在典型工況點附近線性化處理后的系數，若采用LQG、MPC等線性控制策略固然可以在典型工況點及其鄰域內取得較好的控制效果，但不可否認的是，模型參數會隨風速變化而改變，當系統的實際工況點偏離平衡點較大時，線性控制策略的控制性能會大大下降。同時，外部不可測量的噪聲干擾具有隨機性和不確定性，同樣會對系統的控制性能產生較大的影響。為此，本文將非線性模型預測控制與PID控制相結合，提出基于NMPC-PID的獨立變槳距載荷控制策略。PID在外部干擾狀態下具有較好的控制效果；NMPC在處理內部噪聲、模型失配及工作點偏移方面具有一定的優勢[15]。

2.1 基于神經網絡的非線性模型預測控制器

神經網絡具有并行機制、自學習和自適應能力，能夠學習與適應不確定系統的動態特性，具有很強的魯棒性和容錯性[16]。非線性模型預測控制通過控制局部線性化軌跡，使非線性模型找到最小化的目標函數，具有較好的動態控制效果[17-18]。用神經網絡取代系統的非線性模型進行預測，有望實現較佳的預測效果和控制效果。

2.1.1基于RBF神經網絡的風電機組模型辨識

外部干擾、工況點轉移等因素均會導致模型參數攝動，所以式(7)中的A、Bβ、Bu、C、Dβ、Du都是動態變化的。因此，本文采用人工神經網絡對系統模型進行在線辨識，不斷修正線性化模型，以解決模型失配的問題。

圖1 RBF神經網絡結構圖

其中：hj(j=1,2,…,18)為隱含層第j個神經元的輸出，它是一個高斯基函數：

(8)

式中：cj為隱含層第j個神經元高斯基函數的中心向量，bj為隱含層第j個神經元高斯基函數的寬度。

RBF網絡的輸出為隱含層的線性映射：

(9)

式中：wj,i(i=1,2)為第j個隱含層節點與第i個輸出節點之間的連接權值。

圖2所示為利用神經網絡辨識風電機組預測模型的框圖。采用正向建模的方法，RBF神經網絡與待辨識的風電機組獨立變槳距系統具有公共輸入，兩者的輸出誤差作為網絡的訓練信號，通過不斷地訓練使誤差指標盡可能地小，從而使神經網絡的輸出不斷逼近風電機組的實際輸出。其中，誤差指標定義為：

圖2 神經網絡辨識風電機組預測模型的框圖

(10)

采用k-均值聚類算法調整中心向量，采用P-最鄰近算法計算隱含層節點bj的寬度[21]。RBF網絡的隱含層與輸出層之間的連接權值wj,i為[19]：

(11)

式中：η為學習效率，通常取0<η<1[19]。

2.1.2預測模型

預測模型是實現優化控制的前提[22]。在辨識出大型風電機組在不同工況點的系統模型后，在相應工況點利用線性化狀態空間形式即式(7)，可預測風電機組未來的輸出。

(12)

將式(7)等價變換為：

(13)

將式(13)離散化后，得：

(14)

假設塔架的俯仰位移和速度均可測，設控制時域為M，預測時域為P，則由預測模型式(14)可以計算出在控制量為u(k)，u(k+1)，…，u(k+M-1)的作用下未來P個時刻風電機組的預測輸出：

(15)

本文取控制時域M=5，預測時域P=10。

2.1.3滾動優化

針對式(15)中預測輸出，所考慮的風電機組的最佳控制問題可以描述如下：目標是確定從該時刻起的M個控制量u(k)，u(k+1)，…，u(k+M-1)，使風電機組在其作用下未來P個時刻的俯仰力矩和偏航力矩盡可能接近期望值0，同時抑制變槳動作的劇烈變化，從而使性能指標J最小化。J的表示如下：

(16)

約束條件為[23]：

(17)

式(16)等號右側第一項用于懲罰風電機組的俯仰力矩、偏航力矩與參考軌跡的偏差，確保跟蹤誤差最小化；第二項用于優化槳距角的調節，在保證控制性能的前提下，盡量減小變槳動作的劇烈動作。由于變槳執行機構的調節范圍有限，因此需要對槳距角的大小和增量施加約束(如式(17)所示)，以降低其機械疲勞，延長使用壽命。

MATLAB優化工具箱中的fmincon()函數可以處理線性、非線性的等式約束和不等式約束，可用來求解上述優化問題以獲得最優控制序列u(k),u(k+1),…,u(k+M-1)[24]。

按上述方法求出控制量之后，預測控制僅將當前控制量u(k)作用于風電機組，到下一個采樣時刻，再將k+1時刻的控制量u(k+1)作用于風電機組，以此類推，在任一采樣時刻r，都將該時刻對應的控制量u(k+r)作用于風電機組，如此滾動進行，即所謂的“滾動優化”。

2.2 基于PID的反饋控制器

由于狀態變量x(k)可測，故在每一時刻實測到的x(k)可直接用來對該時刻的預測和優化作初始定位，自然實現了反饋校正，故通常情況下不再引入額外的校正措施[22]。實質上，這種自然的反饋是一種狀態反饋，系統狀態變量能夠全面地反映系統內部特性，因此狀態反饋比傳統的輸出反饋更能有效地改善系統性能[25]。

由于大型風電機組的運行環境往往非常惡劣，大氣湍流、塔架振動等各種不確定性外部干擾以及未建模動態均會影響控制效果，使輸出俯仰力矩和偏航力矩偏離期望值，因此有必要采取措施進行補償控制。

PID控制是一種基于偏差的控制，具有原理簡單、使用方便、適應性強、魯棒性強、不依賴于精確建模等優點，因而得到了廣泛的應用。本文在非線性模型預測控制的基礎上，分別在俯仰力矩和偏航力矩通道上各添加一個PID控制器進行閉環反饋調節，對各種不確定性擾動和未建模動態進行補償，以達到加快風電機組響應速度、降低超調、消除穩態誤差的目的。

如2.1.3節所述，為了有效抑制大型風電機組的不平衡載荷，期望的風電機組的俯仰力矩和偏航力矩應設為常值0，故本文中系統的給定輸出為yref=[Mtilt,refMyaw,ref]T=[0 0]T。其控制結構如圖3所示。

圖3 PID載荷反饋控制結構圖

3 仿真與分析

為了驗證所提控制策略，在MATLAB的Simulink中搭建大型風力發電機組模型，然后將所提方法(NMPC-PID)與線性預測控制(MPC)、非線性預測控制(NMPC)分別進行仿真對比。3MW風力發電機組的參數測定是在湍流強度為0.1、風速為18 m/s的情況下進行的[6]。機組的主要參數和氣動載荷系數分別如表1和表2所示。

表1 3MW風力發電機在參數

表2 3MW風機氣動載荷系數

風速曲線如圖4所示，仿真時間為70 m/s，輪轂處的平均風速vhub為18 m/s，湍流強度為A類級別，在0～20 s期間加入最大值為2 m/s的漸變風，以模擬工況點的轉移，20 s以后為相對平穩的風速。三個葉片上的風速分別為vblade1、vblade2、vblade3。

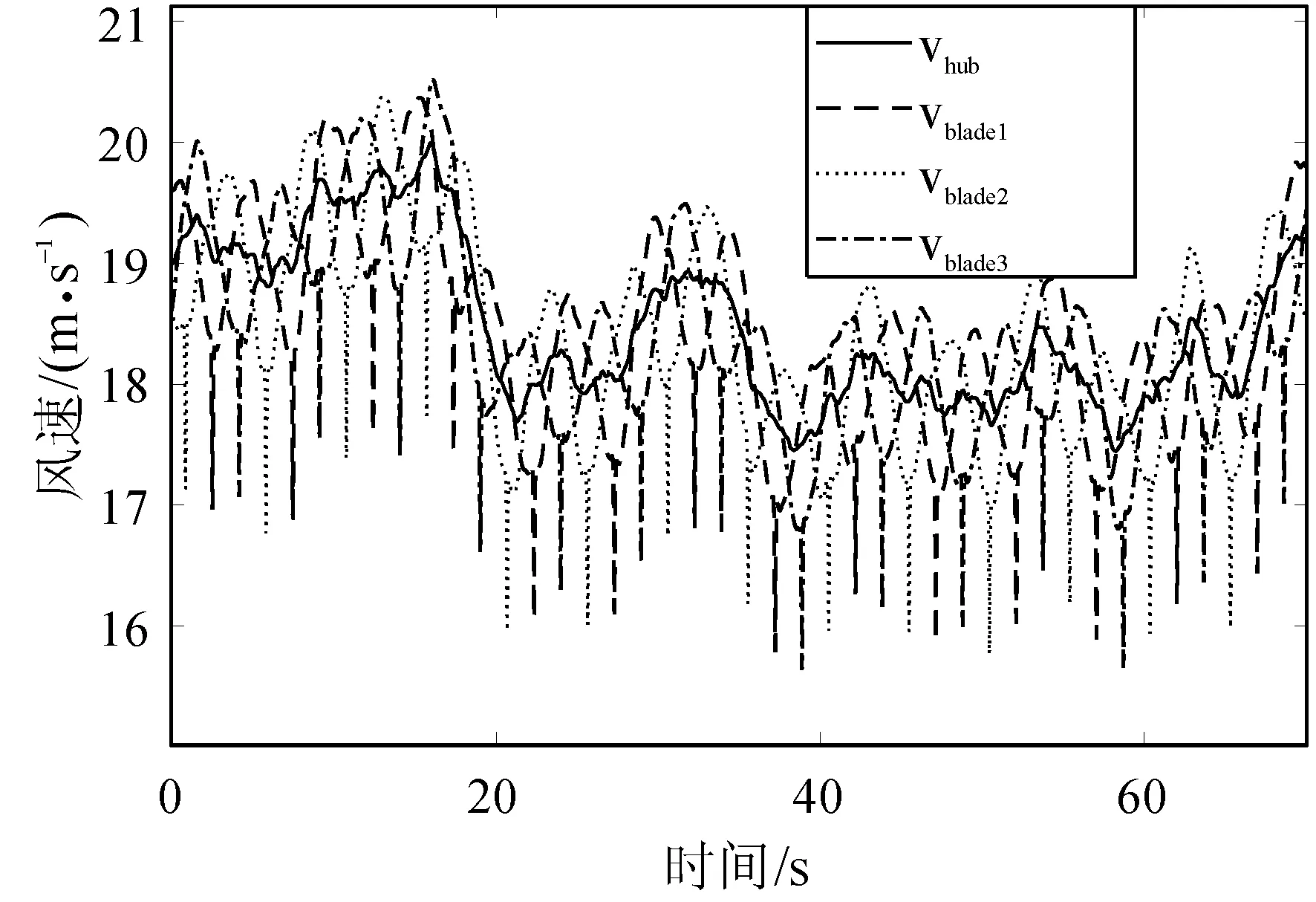
圖4 風速曲線

控制系統優化結果如圖5所示。施加相同的風速條件，在沒有控制器作用的情況下，將模型參數變化±10%，比較實際風電機組模型與辨識出的風電機組模型的輸出。圖5(a)為實際風電機組的輸出俯仰力矩(Mtilt)與辨識出的風電機組的輸出俯仰力矩(Mtilt_identified)的對比圖；圖5(b)為實際風電機組的輸出偏航力矩與辨識出的風電機組的輸出偏航力矩(Myaw_identified)的對比圖。可見，俯仰力矩和偏航力矩曲線的吻合程度是比較高的。經計算，俯仰力矩的均方差約為312.538 Nm，偏航力矩的均方差約為237.549 Nm，相對于其數量級而言很小，辨識精度較高。

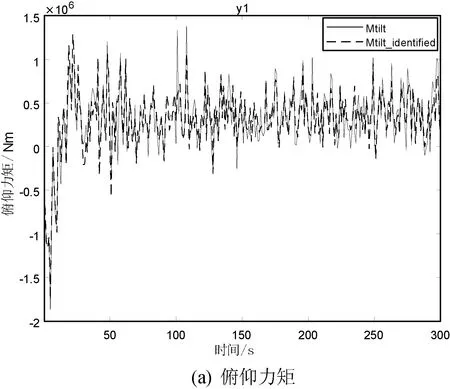
圖5 系統優化結果

為驗證所提控制策略的效果，將其分別與MPC和NMPC進行對比。圖6所示為模型參數攝動導致建模誤差情況下的仿真結果，模型參數的變化范圍為±10%，表3所示為模型失配情況下的性能對比。由圖6(a)和圖6(b)可見，在0～20 s工況點轉移的階段，基于MPC的獨立變槳控制由于只針對典型工況點且依賴于精確建模，故性能有所下降，俯仰力矩出現較大的超調，偏航力矩的波動幅度也有所增加；相對而言，基于NMPC-PID的控制策略由于不斷地對模型進行辨識和校正，從而能夠很好地處理工況點轉移及模型失配帶來的非線性問題，在整個仿真時段內俯仰力矩和偏航力矩具有更好的穩定性，平均值AVG(Mtilt)和AVG(Myaw)分別比采用MPC時更接近期望值0，且波動范圍更小，均方差STD(Mtilt)和 STD(Myaw)分別比采用MPC時減小了78.1%和55.9%。

圖6 模型失配情況下的仿真結果

表3 模型失配情況下的性能對比

圖7所示為外界擾動作用下的仿真結果，通過在俯仰力矩和偏航力矩的通道上添加強度為1×104的白噪聲，模擬塔架、機艙、槳葉振動以及傳感器測量噪聲等各種不確定的、不可測量的外界環境干擾，表4所示為外界干擾情況下的性能對比。由圖7可見，由于NMPC不能預測外部的不可測量干擾，所以NMPC控制下的俯仰力矩和偏航力矩波動范圍相對較大；與之相比，NMPC-PID引入了PID反饋調節對外部干擾進行補償控制，所以俯仰力矩和偏航力矩的變化幅度較小，其平均值AVG(Mtilt)和AVG(Myaw)分別比采用NMPC時更接近期望值0，具有更好的穩態性能，均方差 STD(Mtilt)和STD(Myaw)比采用NMPC時減小了約56.1%和75.6%，具有更強的魯棒性。

圖7 外界干擾情況下的仿真結果

表4 外界干擾情況下的性能對比

4 結 語

本文將非線性模型預測控制(NMPC)與PID控制相結合，用于大型風電機組的獨立變槳距控制。首先運用機理方法對風電機組進行建模，然后針對風機偏離工況點導致模型參數失配而呈現非線性的問題，采用RBF神經網絡對機組模型進行在線辨識和微調，接著采用模型預測控制在存在約束的情況下進行變槳調節，最后采用PID控制對輸出俯仰力矩和偏航力矩進行反饋補償，以克服外界擾動的影響。仿真結果表明，該方法辨識精度較高，具有較好的穩定性和較強的魯棒性，有一定的實際應用價值。但是，該方法只是針對偏離某一典型工況點程度不太大、非線性不太強的情況，如何解決多個典型工況點的控制問題還有待進一步研究。