從一道高考題的思路剖析談高考備考建議

◇ 廣東 黃 惠

2020年高考剛剛結束，今年全國卷Ⅰ解析幾何大題中第(2)小題考查的主要內容是直線與橢圓的位置關系中的直線過定點問題．直線過定點問題是高考的熱點問題，同時也是常規問題，具有一定的綜合性，主要考查考生在“動”中找“靜”的能力，需要考生具有較強的邏輯推理、數形結合、化歸與轉化、數據處理等能力．

直線過定點問題的主要求解思路:要證明直線恒過定點，只需證明直線的方程是直線系的形式(含參數)．根據題設，這個參數可以是動點的橫坐標，也可以是直線的斜率，所以兩種方法本質上是一樣的，不同的是選擇直線方程的哪種形式問題．

1 高考題的解題思路剖析及引發的思考

例(2020全國卷Ⅰ理科20題)已知A，B分別為橢圓的左、右頂點，G為E的上 頂 點為直線x＝6上的動點，PA與E的另一交點為C，PB與E的另一交點為D．

(1)求E的方程；

(2)證明:直線CD過定點．

1.1 高考題的思路剖析

(2)思路1我們會發現點P是主動點，C，D是點P的從動點，那么C，D的坐標可以用點P的坐標表示出來．根據題意，點C，D分別是直線PA，PB與E的交點，故聯立直線與曲線方程即可，這樣點C，D的坐標就都跟某個參數有關，即直線CD的點斜式方程只含一個參數(注意要考慮參數的值是否會使斜率不存在的情況出現)，這樣就可以找出定點．

解法1由(1)知A(－3，0)，B(3，0)，設P(6，t)，C(x1，y1)，D(x2，y2)，則直線PA的方程為y＝聯立方程得

思路2要想證明直線CD恒過定點問題，只需確定直線CD的直線系方程，為了減少參數個數，可設直線CD的方程為y＝kx＋m(斜率不存在時，單獨證明)，通過題目已知條件找出k與m的關系．要找出k與m的關系就必須列出關于k，m的等式，通過分析可知等式來源于直線AC，BD相交于點P．

解法2當直線CD斜率不存在時，設直線CD:x＝n，則由(1)知A(－3，0)，B(3，0)，設P(6，t)，由kAC＝kAP得

同理，由kDB＝kPB得

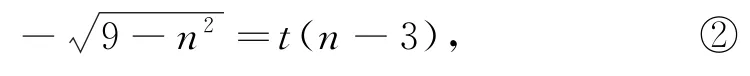
當直線CD斜率存在時，設直線方程為y＝kx＋m，聯立方程

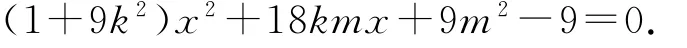
設C(x1，y1)，D(x2，y2)，則

直線AC的方程為把x＝6代入同理，由直線BD得P(6，化簡得

把③④代入⑤，得

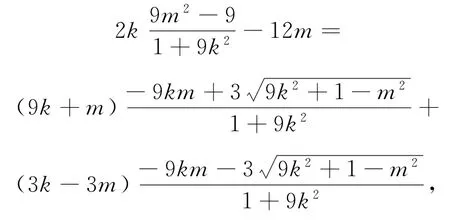
把含有根號的放到等式的一邊，整理得

1.2 引發的思考

縱觀近幾年解析幾何大題，不難發現，高考考查的知識點和能力點都沒有超出通性通法的范疇，由此引發如下三點．

1)認清解析幾何的本質

要引導學生利用代數來研究幾何問題，通過幾何圖形反映代數形式．要關注學生對幾何圖形的掌握情況，是否會用圖形語言來表達幾何問題，同時，要關注學生是否會用代數方法來研究幾何問題．

有了總體框架之后，立足于學生是否會操作，有沒有掌握幾何問題“解析化”的過程，從方程、數值、圖形中是否能找到幾何對象，分析其特征，找到代數的方法，通過代數結果，得出幾何結論．

2)重視基本問題

圓錐曲線中最基本的兩個問題，一是曲線的定義，二是曲線標準方程的來源．其他問題都是在這兩個問題的基礎上產生的，所以一定要重視定義的形成過程和方程的推導過程，直線與圓錐曲線的位置關系中常見的模型主要有相交弦長問題、與弦長有關的三角形和四邊形問題、定點和定值問題、與向量結合問題等，這些都要有所積累，研究這些問題中的共同特征，掌握基本的解決問題的方法．

3)注重解題策略

解析幾何問題考查難度屬于中上水平，涉及數形結合、邏輯推理、數學運算等能力，要得出最后結果對學生來說困難重重，所以平時要從這些方面入手:如何引入參數，引入參數的原則是什么(盡量減少參數個數，聯系所學的基本模型列出等式，簡化運算)；如何設計運算思路，即優化解題過程，關注運算的對象，識別題目所存在的模型有哪些(定點、定值、弦長有關的最值、范圍問題等)；如何更接近最后的結果，代數方法的選擇(函數與方程思想、設而不求、根與系數的關系、判別式、整體消元等)．雖然題目的問法可能不同，但是掌握一定的策略之后就可以順利求解．

2 高考備考建議

1)要在理解知識點本質的前提下掌握有關考點

高考試題中，有直接考查知識點簡單記憶的試題，但更多的是在對本質理解的基礎上對知識應用的考查．例如，“直線方程”部分，從宏觀的角度看，其本質是兩種轉化，即“幾何問題代數化”和“代數問題幾何化”；從微觀角度看，直線方程的5種形式中，“點斜式”的本質是“已知點和斜率就可以確定直線方程”和“已知直線方程的點斜式就可以確定直線的斜率和其經過一點的坐標”．

2)要注重“思路分析”的邏輯性

任何數學問題的解決都要注意兩點，首先是思路的切入點，比如本文試題中第(2)題的切入點非常重要；其次是在找到切入點后的分析過程中遇到思維受阻時如何突破的問題．比如今年全國卷Ⅰ的導數應用問題，其切入點非常容易找到，即分離參數，但分離后的函數求最值過程中，針對導函數的最值點判斷思維容易受阻，突破的方式就是通過不等式放縮將超越式轉化為代數式．

3)要注重“通性通法”

高考試題的解法大多數都在“通性通法”的范疇內，所以在備考中要注重“通性通法”，這樣不但可以避免“刷題”的勞累和備考的低效，還會產生“以不變應萬變”的自信．

4)要關注“易錯點”

高考考查的目標中包括考查“思維的嚴謹性”，所以在備考中一定要關注每個知識體系或知識塊中的“易錯點”．