用好學習材料 發展思維能力
——《20以內進位加法》相關教學再探索

張 慧

數學教育“既要使學生掌握現代生活和學習中所需要的數學知識與技能，更要發揮數學在培養人的思維能力和創新能力方面的不可替代的作用”。好的教學，與其說是找到了好的教學方法，不如說是精心準備了合適的學習材料。鮑建生教授在指出：培養學生的思維能力，關鍵是學習材料的設計。本文以《20 以內進位加法》教學為例，談談算法多樣化和以代數思維啟發為手段，培養學生思維能力的教學路徑。

一、探索多樣的算法，培養思維能力

算法多樣是在運算教學中培養學生思維能力和創新能力的重要路徑之一。新思維數學積極倡導在學習標準計算程序的同時把訓練重點從習得運算技能轉向思考性訓練，培養學生的創新意識，給學生提供創新機會，幫助學生積累創新經驗。鼓勵學生探索多樣化的算法應當作為運算教學始終如一的教學目標，關鍵在于問題情境的設計以及教學反饋的組織。《20 以內的進位加法》是新思維數學一年級上冊新授課的最后一個單元。此時，學生已經掌握10 以內的加減法、10 加幾和十幾減幾，而這一內容也是以后學生學習多位數進位加法的重要基礎，在加法學習中起著承上啟下的作用。如何在教學中滲透數學思想，發展思維呢？筆者對《20 以內的進位加法》做了如下設計——

師：同學們玩過飛鏢嗎？你們喜歡玩嗎？不僅你們喜歡，森林里的小動物們也非常喜歡玩呢！森林運動會的射擊比賽就要開始了，狐貍裁判再一次邀請我們去觀看射擊比賽，大家愿意去看看嗎？

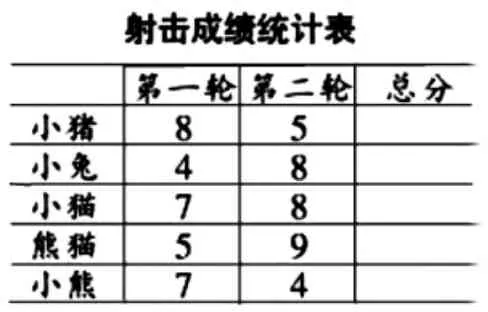
課件演示：射擊比賽場景；小動物爭第一的場景；射擊成績表。

師：究竟誰是第一名呢？（學生猜測）到底誰是第一名，我們有什么辦法可以確切地知道？

?

生：通過計算可以知道。

師：我們先算誰呢？先算小豬好嗎？怎么列式？

生：8+5。

（學生獨立計算）

方法1：10＋5＝15，9＋5＝14，8＋5＝13。

方法2：8 ＋2 ＝10，2+3 ＝5，8 ＋2+3=13。

方法3：5＋5＝10，5＋6＝11，5＋7＝12，5＋8＝13。

方法4：8＝10－2，8＋5＝10＋5－2＝13。

方法5：5 ＋5 ＝10，5 ＋3 ＝8，8 ＋5＝5＋5＋3＝13。

（學生匯報交流）

師：小組討論，哪些方法你能看懂？哪些方法你有不懂的要提出來。選擇能解釋的方法來說一說。

生：方法1 一個一個地推。10加5 等于15，那么9 加5 少了1，是14，8 加5 就再少1，是13。

生：方法3 兩個5 相加是10，5 加6 多1 個是11，5 加7 多2個是12，5 加8 多3 個是13。

生：方法5 把8 里面分出5，兩個5 相加是10，10 再加上3 就是13。

師：你們都解釋得很好。有沒有不懂的問題？

生：方法4 為什么要減2 呢？

師：算加法怎么會跑出減法來呢？

生：把8 看成10，就多了2。10+5 是15，再把多加的2 減去，就是13。

師：真能干，不僅自己會算，還能解釋別人的算法。再來一個更有挑戰性的問題，哪些方法有共同點？

生：方法1、2、3 都是根據我已經會算的算式，然后根據之前學過的規律，其中一個加數不變另一個加數增加或者減少，和也相應增加或者減少。

師：這是一個算式推導出來的。能利用我們學過的知識解決問題，這是一個好方法。

生：方法4、5 都先湊出一個10，然后再用我們之前學過的10加幾和十幾加減幾來計算。

師：你們給這種方法起個名字吧。我們叫“湊十法”。

師：湊十法的兩種方法有什么相同點和不同點？

生：相同點是都要找到10。

生：不同點是第一種湊十法是找8 和幾湊十，第二種湊十法是找5 和幾湊十。

師：方法2 是看大數拆小數；方法5 看小數拆大數。

師：我們在計算的時候可以拆大數也可以拆小數。

師：今天我們學習了“湊十法”，誰能根據雞蛋的情境圖說得更具體一點？

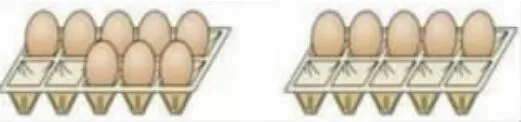
生：從5 個雞蛋里取2 個，放在8 個雞蛋的蛋架里，8 和2 湊成10，10 再加剩下的3 等于13。

生：我們是這樣想的，從8 個雞蛋里取5 個，放在5 個雞蛋的蛋架里，5 和5 湊成10，10 再加剩下的3 等于13。

對于大多數一年級上學期的學生來說，他們在教師正式教學20 以內進位加法之前，都已經能正確地算出答案。本課教學的目標不能局限于算出結果，或是追求算得又對又快，更為重要的是通過算法多樣來發展學生的思維能力。算法多樣并不是對一個學生的要求，而是對全班學生集體思考的要求。教學只要留給學生足夠的時間去思考，學生就會想出很多的計算方法。進一步，組織學生理解這些不同的方法，獲得廣泛的解決問題的思路，積累解決問題的經驗，這既是算法多樣的教學目標要求，也是通過算法多樣發展學生思維能力的路徑之一。

那么，學生何以產生如此豐富的思考呢？

一是前期教學打下的基礎。主要基于兩個方面：其一，在學習10 以內的加減法時，掌握了對一個數進行靈活拆分的方法。其二，在認識十幾的數時經歷了豐富的圈十數數的活動。在這樣的活動中，不僅有利于學生概括十幾的數的組成，同時也積累了十加幾就是十幾的思維經驗。

二是得益于本課的問題情境。教材提供的放雞蛋的蛋架，是有結構設計的，學生根據已經放的雞蛋和留存的空位，容易產生湊十的思路。這也就是說，好的計算情境，不僅能從情境中引出要計算的題目，還要能對算法的探索提供智力支持。

二、萌發代數思維，培養思維能力

學生對數學知識的理解及能力發展不是一蹴而就的，是有一個逐步提高的過程。新思維小學數學教學體系，致力于使學生在學習重要知識與形成能力時，像“滾雪球”那樣滾動發展，經歷由淺入深、由小到大、逐步積累的過程。

眾所周知，算術和代數知識是兩個不同階段的學習內容，通常是先學習算術，到了高年級才開始學習代數，導致了算術和代數學習的脫節，這可能是影響學生從算術思維轉向代數思維困難的重要原因。新思維小學數學從一年級開始就把算式計算與代數運算有機整合，促進代數思維的早期萌發。

在20 以內進位加法的練習課中，筆者設計的練習是8+7=10+（ ）。對于初次接觸這個問題的一年級學生來說，這是一個頗具挑戰的數學任務，學生需要重構對等號的理解：即把等號從原來所理解的“得到答案”調整為“左右兩邊平衡”。事實上，對等號的兩種不同理解，在一定程度上代表了算術思維與代數思維的差異。

一般來說，學生習慣于看到一個算式，馬上算出一個答案，如果這個問題設計成8+7=（）+10，那么在括號內填15 的學生將會很多。考慮到代數思維早期萌發是一個有挑戰性的研究課題，學生習慣于根據既定的程序進行計算，而不善用“平衡”來思考上述問題，我們給出了如8+7=10+（）這樣的形式。

師：你在括號里填了幾？請你仔細地想一想，并說明理由。

生：我填了5。

師：你是怎么想的？能與大家分享嗎？

生：我是這樣想的：先算左面的和是15，再想10 加幾是15，10+5=15。

生：先算左面的和是15，再算15-10=5，所以括號里填5。

師：先算出左邊的得數，再用它減10。哪些同學也是這樣想的？

師：還有不一樣的想法嗎？

生：我是這樣想的，可以把8看成10，這里多加了2，另一個加數就要減2，所以括號里填5。

師：這位同學的想法可行嗎？為什么括號里的數比7 少2 呢？

生：因為把8 看成10，多看了2，所以另外一個加數7 要減去2，保持平衡。［使用天平進行直觀演示：先在天平兩邊都放上兩袋（8+7）個小球，然后在天平右邊一個口袋里再放入2 個小球］

師：想要天平平衡，右邊另一個小袋里應該——

生：拿出2 個小球。

師：還有別的想法嗎？

生：可以想把7 變成10，這樣等于多加了3；另一個加數8就要減3，所以括號里填5。

學生解決這個問題的意義，主要不在計算上，而在于對等號的理解上。對等號的理解是從算術思維走向代數思維的關鍵步驟。在小學數學中，學生第一次接觸等號是在數的大小比較中，得到兩個數的大小比較關系。之后一直在運算中使用等號，如：1＋2＝3，因此學生很自然地將等號與得出結果聯系在一起，把等號看作一種運算符號。而在代數思維中，等號的意義需要從“得出”拓展為“等價關系”。對于等價關系的理解，亦不僅局限在兩邊結果相等上，更應該關注到等式中的“結構”關系，即8→10 增加了2，如果要保證等式平衡，那么7就應該相應地減少2，得到5。從通過計算結果來判斷到通過分析關系來判斷，學生的代數思維又進了一大步。

在教學中，我們需要創設既能聯系基礎又能拓展思維空間的開放教學情境，把加強基礎知識與培養思維有機地結合起來，落實到具體的課堂行動中。