幾何直觀讓課堂“活”起來

彭愛華

幾何直觀主要是指利用圖形描述和分析問題。借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路、預測結果。如何在課堂上利用好幾何直觀，從而達到滿意的教學效果呢？

一、借助幾何直觀揭示數學知識的形成過程

教學《圓柱的體積》時，教師先出示裝了水的圓柱容器，并引導學生思考：容器里面的水形成了什么形狀？（圓柱），你能用以前學過的辦法求出這些水的體積嗎？通過分組討論，學生匯報：把水倒入長方體容器中，量出數據后再計算。接下來，教師出示圓柱的模型，繼續引導學生思考：“該如何求圓柱的體積呢？”六年級學生已經有了一定的轉化思維，會想到把圓柱轉化為已學過的立體圖形。但是，如何轉化呢？筆者利用課件進行直觀演示：根據圓的面積公式的推導方法，先把圓柱底面分成若干相等的扇形，然后把圓柱切開，再拼起來，就近似于一個長方形，學生通過觀察，分組用模型進行實際拼接，找到了圓柱體積的計算方法：發現圓柱的體積與圓柱的底面積和高有關，只要知道圓柱的底面積和高就可以直接用底面積乘高來計算，如果不知道底面積，只知道r、d或c，也可以先計算出底面積再來求體積。

接下來，在解決教材30頁第14道習題時，考慮到很多學生很難憑空間想象找準長方形旋轉和卷曲后得到的圓柱的底面半徑、底面周長、高和長方形相應邊的對應關系。所以，在完成這道題之前，筆者讓學生提前準備好了兩張同樣的長方形彩紙，讓學生親自動手轉一轉、卷一卷，很快的就找準了對應關系，根據面動成體的道理，學生發現：以長為軸旋轉一周，得到一個底面半徑為10厘米，高為20厘米的圓柱體，以寬為軸旋轉一周，得到一個底面半徑是20厘米，高為10厘米的圓柱體，再根據圓柱的體積公式得到解題方案，通過教具輔助，問題便迎刃而解。

二、借助幾何直觀理解問題的本質

教材這一章的例題是求不規則圓柱的體積，這樣的問題不是學生常見的問題，該如何入手呢？筆者先帶領學生回顧了不規則物體體積的求解方法，接著，筆者再出示帶來的礦泉水瓶并提出問題：“這瓶礦泉水的標簽沒有了，要怎么求出瓶子的容積呢？我們能用公式直接計算出來嗎？”然后，請學生拿出事先準備好的瓶子觀察、思考正著放和倒著放的瓶子中哪些量沒有變。幾分鐘后，小組匯報結果：1.水的體積沒有變;2.瓶子空著部分的體積沒有變;3.瓶子的體積沒有變。緊接著，筆者拋出以下問題：“我們能將這個不規則的圓柱的體積轉化成規則的圓柱體積嗎？轉化后圓柱的體積和原來瓶子的體積相等嗎？”通過學生的觀察和實踐，他們已經有了解題思路，瓶子的體積就是正立時水的體積與倒放時空瓶的體積之和。

這樣的實物演示把不規則圓柱轉化成了規則圓柱體，讓學生一下子就找到了解決問題的關鍵所在，學習興趣也調動起來了。

再比如，遇到需要把動態的水流想象為靜態的圓柱的題目時，圓柱的高度隨時間在變化，部分空間想象力較差的學生想象不出來，這時，筆者出示課件演示圖，學生很快明白過來：流出來的水就是一個圓柱體。有了這個認識，學生很快會發現：一秒鐘流出的水的多少實際就是一個底面直徑1.2厘米、高20厘米的圓柱的體積，而50秒流出的水的體積就是50個這樣的圓柱的體積總和，也可以把50秒流出的水想象成一個底面直徑1.2厘米、高為1000厘米的圓柱。

三、借助幾何直觀形成解決問題的最佳策略

在教學中遇到較復雜的實際問題時，教師可以借助幾何直觀幫助學生分析、理解題意，最終形成解決問題的策略。以下面這道題為例。

這道題是知道側面積和底面周長，求該圓柱的體積。根據平時的解題思路，學生都會先根據側面積求出高，再利用圓柱的體積公式計算出體積。當學生都計算出來后，筆者追問：“還有其他更簡單的方法嗎？”學生都愣住了。接下來，筆者出示了如下圖形，讓學生自己觀察，看能發現什么。

這是圓柱體積公式推導時用到的把圓柱轉化成長方體的方法，筆者把長方體換了一個方向，底面換了一個面并標注出來，并拋出了一個問題：“現在的長方體底面積是圓柱的哪個部分？高又是圓柱的什么？”學生觀察了兩分鐘，部分學生發現：現在這個長方體的底面積是圓柱側面積的一半，而高是圓柱的半徑。筆者再讓學生用這種方法來算一算，果然簡單多了，直接用側面積的一半乘以半徑。教師要有意識地引導學生學會看懂圖示語言，體會示意圖既簡潔又形象的特征，能為解決問題提供清晰的思路，讓學生對圖示語言產生探索欲望，培養學生運用“幾何直觀”的意識。

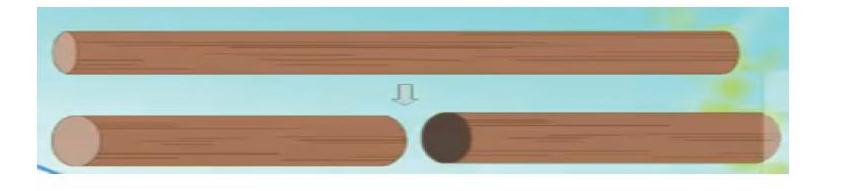
再比如，教師繼續出示如下例題：把一根長3米的圓柱形木料截成兩段后，表面積增加了25.12平方厘米，求原來這根木料的體積是多少？解決這道題的關鍵在于求出這根木料的底面積，而底面積該怎么求呢？如果教師出示下面的直觀圖，學生能很快地得出：原來的底面積就是增加的表面積的一半。

幾何直觀是一種能力，也是一種方法，要讓學生具備這種能力，需要教師不斷探索，當遇到學生難以解決的問題時，不妨利用圖形進行觀察和演示，讓抽象的概念在學生大腦中形成直觀的印象，從而提高運用幾何直觀解決問題的能力。

（作者單位：松滋市八寶鎮豐收學校）

責任編輯 ?張敏