神經網絡全局勢函數在多相催化中的應用

馬思聰，劉智攀

（復旦大學化學系，上海200433）

自20 世紀90 年代開始，隨著計算機技術的發展和量子力學的深入研究，多相催化理論計算逐漸成長為一門獨立的學科，為催化領域的發展添磚加瓦。理論催化的最大優勢在于其研究的角度是從原子和分子層面出發的：構建催化劑結構模型、研究反應物分子的吸脫附行為、探索不同反應路徑來確定化學反應動力學，最終構建出催化劑結構與催化性能之間的關系。

“構建催化劑結構模型”寥寥幾個字背后是一片高度復雜的荊棘叢林。材料結構的模擬和預測是理論化學研究中一大重要方向，只有熟知材料結構才能有的放矢，實現后續的化學反應研究。材料結構模擬的難點在于其復雜度上，N個原子的體系有3N 個坐標，不同的坐標可以產生無窮種可能的結構，如何搜索到熱力學合理的結構一直是這一領域的難點。目前已發展出很多比較成熟的勢能面采樣方法，包括隨機表面行走（stochastic surface walking，SSW）、遺傳算法（genetic algorithm）、盆地跳躍（basin-hopping）等（具體在第1 節詳細介紹）。在實際應用中，勢能面搜索通常都是基于第一性原理方法來計算能量和力。雖然該方法得到的勢能面比較準確，但本身的計算速度太慢，獲得一個結構的能量和力的計算代價過大。因此，為了更快地遍歷勢能面，可以從改變能量計算方法角度來著手。目前，比較有前途的措施就是把第一性原理方法改成力場方法。采用力場方法可以實現對勢能面的快速搜索，比第一性原理方法快103～105 倍，但力場方法的精確度一直備受詬病。如何構造出實用的力場一直是目前的研究重點。在構造力場的方法中，神經網絡（NN）是一種強大的擬合工具，可以根據已有數據表達能量和結構之間的函數關系，從而實現預測功能。既獲得了計算精度，又可以實現計算速度的提高。目前，本文作者課題組開發了LASP（large-scale atomic simulation with neural network potential）軟件用來解決相關的技術問題[1]。LASP 核心優勢在于：①可以利用神經網絡進行勢能面模擬計算；②提供了SSW 勢能面采樣工具；③提供了高效的雙端表面行走方法（double-ended surface walking method，DESW）過渡態搜索工具。

1 SSW-NN方法介紹

1.1 勢能面結構搜索方法介紹

在Born-Oppenheimer 近似下，整個體系的能量可以看成與原子核坐標相關的函數。N個原子的體系具有3N個自由度，體系的能量可以看成3N維空間的超曲面，這個超曲面叫作勢能面。圖1顯示了一個三維投影的勢能面示意圖。這個勢能面有幾個需要注意的地方：首先是能量的局域極小點，這幾個點的一階梯度為0，Hessian 矩陣（二階梯度）的本征值全部為正值。這些點一般都是代表著穩定結構，有可能在實際中被合成出來。其次是幾個鞍點，這幾個鞍點的一階梯度為0，但是Hessian 矩陣的本征值中有一個為負值，意味著在這個方向它是不穩定的，這些鞍點也被稱為過渡態。對于化學反應研究，勢能面采樣的核心就是如何快速得到極小點和鞍點。

圖1 三維勢能面示意圖

假設有一個結構A，這個結構并不是極小值點。此時，為得到A結構附近的極小值點結構，需要對結構A進行能量極小化，這個過程叫作結構優化。由于每個極小值點就是一個勢能面上的“坑”，所以結構優化更通俗地講叫作“入坑”。“入坑”的方法有很多，包括共軛梯度算法（conjugate gradient）、牛頓法（Newton method）、準牛頓法（quasi-Newton）和Broyden 方法等。“入坑”的方法只適用于從一個點出發搜索局域穩定結構，對全局勢能面搜索則沒有助益。因此，必須要有“出坑”的方法來擴大搜索范圍。目前在“出坑”方面已開發出大量方法。盆地跳躍算法[2-3]是基于在某一隨機方向上添加微擾，然后進行結構優化以及最后通過蒙特卡洛（Monte Carlo）選擇過程來確定是否接受新結構。基本步驟為從當前結構出發，在某一方向上隨機移動原子，并對移動后的結構進行幾何結構優化，然后根據一定標準來決定是否接受新結構。整個算法就相當于是在一個個盆地里面來回跳躍。元反應動力學（metadynamics）算法[4-5]是在分子動力學的基礎上，往勢能面上添加偏置勢函數來變相降低跳躍能壘，加快翻越勢能面的速度。遺傳算法[6-7]是選取一系列結構（親代），通過結構之間的相互組合、交叉、變異從而產生出新的結構（子代）。再根據能量篩除高能量結構，保留低能量結構。通過反復的迭代，實現勢能面結構遍歷和搜索。粒子群優化（particle swarm optimization）算法[8-9]則采用一群結構，對這群結構給一個向著能量最低結構的微擾方向來產生新結構。模擬退火（simulated annealing）[10-11]則是沿著在某個方向行走并產生一個不斷升降溫的蒙特卡洛選擇過程來確定是否接受新結構。極小值跳躍（minima hopping method）[12]采用分子動力學方法，在相同能量的極小值結構附近不斷升溫，使原子位置偏離極小值結構從而產生新結構。本文作者課題組發展了SSW方法來搜索勢能面[13-14]，主要借鑒了元反應動力學方法中添加偏置勢函數的思想，不斷添加勢函數使其可以翻山越嶺。在各類算法中，有些側重于尋找新結構，有些側重于尋找結構之間的相變路徑。一般來說，這兩種是互斥的。道理很簡單，越傾向搜索產生新結構的方法，其對原有結構的依賴越小，可以隨意地變化坐標位置，也就無從談結構之間的關聯性。而尋找結構之間關系的方法，則對原有結構非常依賴，搜索范圍也就局限在原有結構附近，搜索效率降低。

1.2 SSW方法

SSW 方法是基于偏置勢函數驅動分子動力學的思想發展而來的。整個SSW過程包含三個步驟，即爬山步驟、優化步驟和蒙特卡洛判斷步驟，其中核心是第一個爬山步驟。具體來說，首先從一個穩定的結構點出發，在某一隨機方向添加偏置勢函數。添加的高斯勢函數用式(1)來表示。

式中，NG 為添加高斯勢函數的個數；R 是結構的坐標向量；Vreal是真實的勢能面；Rtn是添加n次高斯勢函數以后的結構坐標向量。高斯勢函數的大小和寬窄用w 和ds 來控制。然后優化這個方向，使得這個方向的振動頻率比較低。繼續隨機添加偏置勢函數，優化方向。反復迭代到一定次數后，撤去偏置勢函數，利用“入坑”方法優化到底，最后通過蒙特卡洛過程來決定是否接受新結構，見圖2。真實的勢能面用黑色實線表示，從一個局域極小值到另一個局域極小值是通過一步一步在某個方向上添加高斯勢函數實現的。目前SSW 方法已經可以實現晶體、 團簇、 分子和表面結構搜索[13,15-17]。

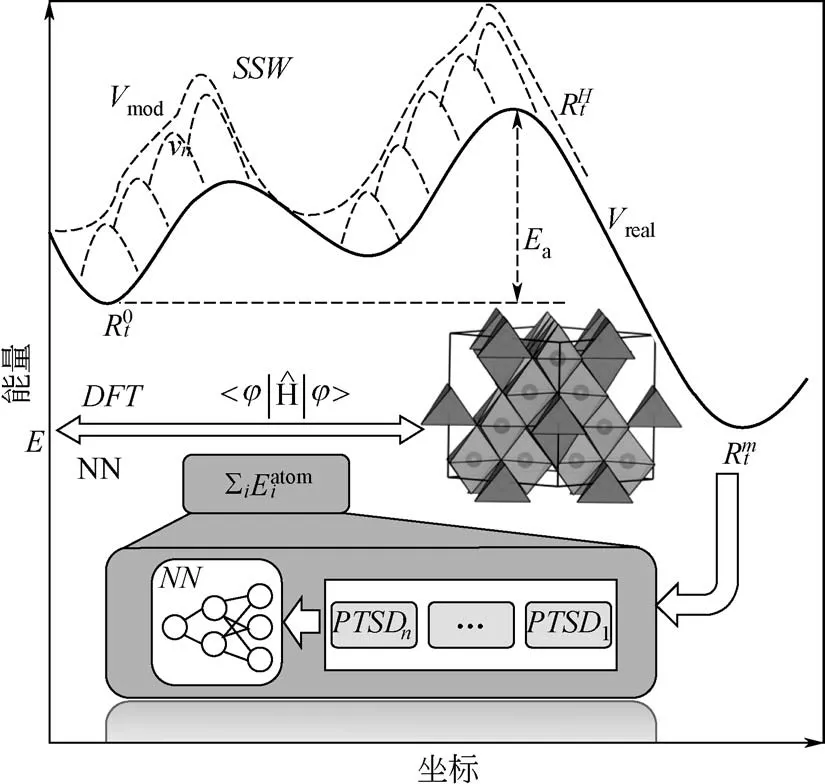
圖2 SSW-NN示意圖

1.3 NN方法

1.3.1 NN架構

神經網絡作為一種強大的擬合算法，近年來為催化領域帶來了新的輝煌[18]。它最初是用來研究大腦中的信號處理[19]。在接下來的幾十年里，神經網絡已經發展成為一類廣泛的算法，在數字預測、模式識別和數據分類等領域有著廣泛的應用。通過非線性“黑盒”數據處理，自動搜索獨立或非獨立變量與目標值之間的函數關系。目前，人們已經嘗試利用神經網絡來預測化學性質，例如振動光譜[20]、力常數[21]、兩分子的反應散射、單分子分解反應和氣體分子在表面上的吸附等[22-23]。因此，神經網絡在搜索結構和解決反應活性位點方面顯示出巨大的潛力。

圖3顯示了一個最簡單的Feed-Forward 神經網絡（FFNN）的工作原理。整個網絡由許多神經元或按層排列的節點組成。輸入層中的節點輸入所有可提供的信息（xi）。輸出層節點的最終值（y）是xi的一個解析函數。而函數形式則由隱藏層的數量和每個隱藏層的神經元數量決定。圖3采用線性方程組形式和矩陣形式列出了數據是如何在FFNN傳遞的。值得注意的是，每一個獲得的值（yij）都應該被一個非線性活化函數來活化。神經網絡的核心是獲得在基于梯度的迭代優化算法下確定的最優參數（wikj）。一個好的神經網絡勢函數受許多因素的影響，例如隱藏層的數量、每個隱藏層的神經元數量、活化函數和優化算法。在實際應用中，采用幾種不同的網絡結構來構造神經網絡，分析結果，選擇最佳網絡結構是最有效的方法。在早期，FFNN結構被引入化學領域。輸入層中的節點以坐標向量（如笛卡爾坐標或帶距離和角度的內部坐標）的形式來描述化學結構，輸出層是總能量。這就要求訓練集必須具有相同數量的原子，才能在神經網絡勢函數中保持相同的輸入層節點數。所得到的神經網絡勢函數也只能用于原子數與訓練集相同的系統，導致FFNN勢函數沒有實際的預測價值。

2007年，Behler和Parrinello首先實現了高維神經網絡框架（HDNN）以滿足實際應用，該框架可適用于含有數千個原子的高維系統（圖3）[24-25]。在這種框架中，通過拆分，使每種元素具有一個FFNN，一個體系中的每個原子分別進入各自對應元素的FFNN來得到目標值。通過這種構想可以克服早期FFNN勢函數不可擴展的問題。每個原子可以提供一個原子能量Ei，總能量便可寫成所有原子能量的加和，見式(2)。

HDNN框架適用于任意數量的原子：如果一個原子從系統中被移除，它所對應的原子神經網絡就會被刪除；反之亦然。具體的詳細過程見圖3和其他參考文獻[26-28]。HDNN 和FFNN 最大的區別是輸出層，其中原子能和總能量分別是HDNN 和FFNN的目標值。HDNN的困難在于如何獲得原子能。幸運的是，真正的原子能不需要精確計算，HDNN可以自動地將總能量拆分成“假”的原子能。因此，HDNN中最重要的是如何描述輸入節點中的原子環境。如Behler等[24]所建議的，用于描述原子環境的輸入節點通過解耦將局部環境中原子的笛卡爾坐標轉換成特殊類型的多體結構描述符（Gi）。這些結構描述符提供了系統中每個原子的相鄰原子的徑向和角度排列信息。一個好的結構描述符必須是一個單值函數，每個不同的原子環境對應不同的值，并且它們必須是連續和可微的，以便能夠計算力的解析導數。

原子力可通過式(3)來計算得到[29]。

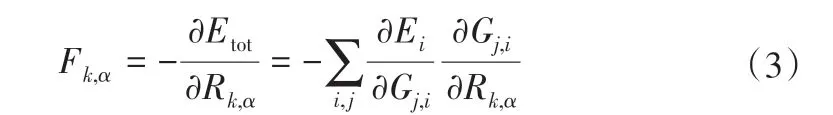
式中，Fk,α是作用在k 原子上在α（α=x，y，z）方向上的力；Rk,,α為原子坐標。結合式(2)可以得到Fk,α與Gi之間的關系。

類似地，靜態應力張量矩陣元σαβ可以由式(4)得到。

式中，rd和rd分別為距離向量和它的模；V 是晶體結構的體積。

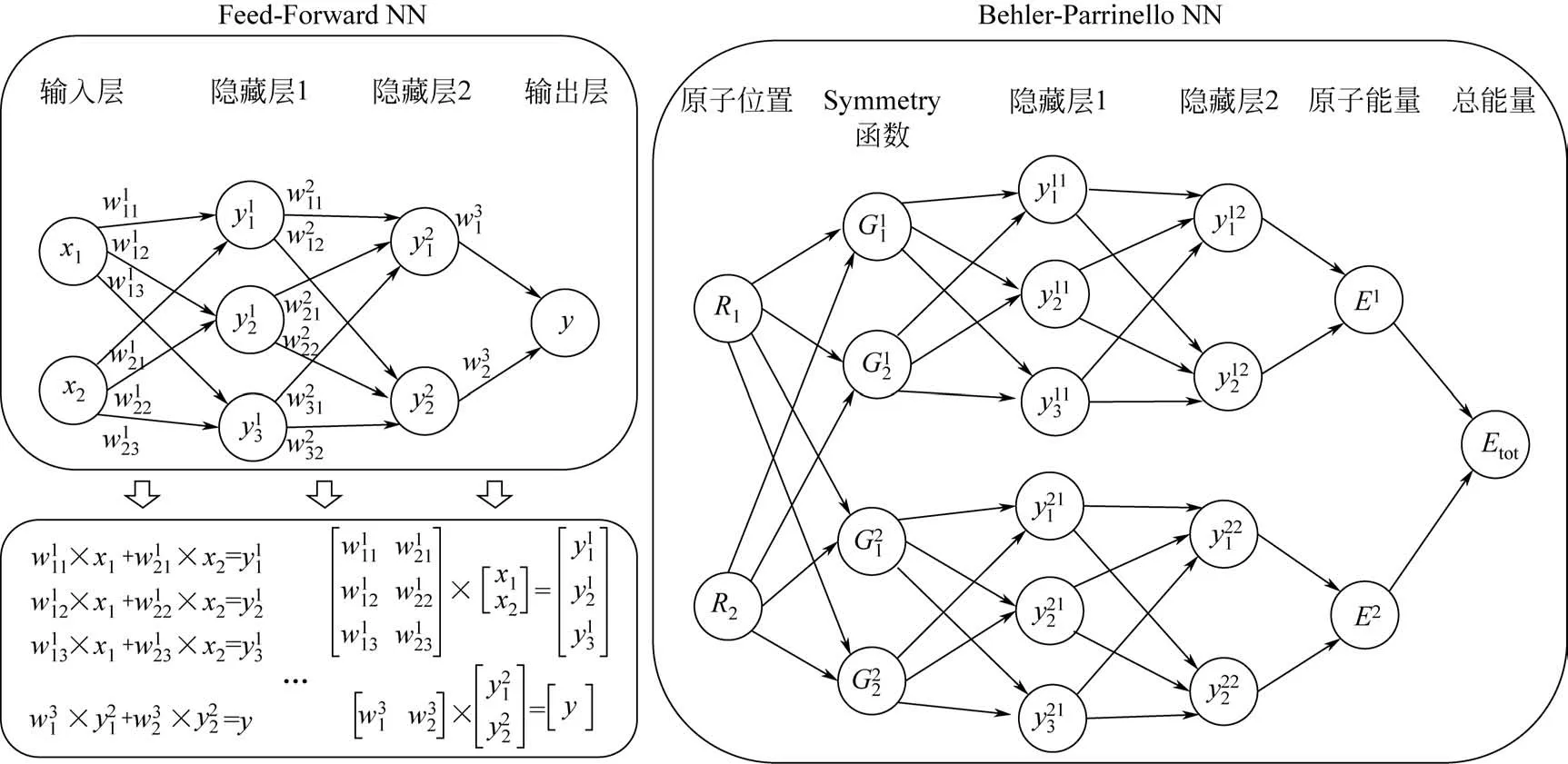
圖3 Feed-Forward和Behler-Parrinello神經網絡框架

一旦確定了網絡架構，下一步就是確定每個NN 子網中的權重和偏差（NN 參數），這個過程稱為NN訓練。對于具有兩個隱藏層的標準FFNN，每個隱藏層有40 個節點，那么權重和偏差的數量通常為104～106。為了訓練如此大量的神經網絡參數，需要定義一個性能函數Jtot[29-30]來測量神經網絡輸出相對于訓練集真實值之間的偏差，見式(5)。訓練過程將使Jtot最小化，直到神經網絡預測屬性的精度達到預設標準。

式中，ρ=1～100和τ=0.1～1。這允許Jtot可以同時訓練能量、力和張力。在實踐中發現，對于固體的全局優化，力和應力都需要精確，最方便的方法是允許神經網絡訓練同時或獨立地調節式(5)中的三項參數。

目前許多基于梯度的優化算法已經被用于優化網絡權重和偏差，如隨機梯度下降（SGD）[31]、共軛梯度（CG）[32-33]、Levenberg-Marquardt（LM）[34]等。一般認為，準牛頓二階方法，如L-BFGS和LM會更快地收斂到真正的極小值。值得一提的是，與使用量子力學計算生成數據集的工作量相比，神經網絡的訓練實際上不是整個過程的速度決定步驟。

1.3.2 結構描述符

在原子的笛卡兒坐標到結構描述符的轉換過程中，必然要在某一半徑處做截斷，導致結構信息的丟失，因此應通過選擇合適的結構描述符來小心地減小這種誤差。作為在HDNN中將結構與其能量相關聯的關鍵，要求一個合格的結構描述符必須要足夠敏感，以盡可能地區分勢能面上的每個結構。Behler 和Parrinello[24]提出了高斯型結構描述符（GTSD），式(6)～式(8)中描述了最常用的兩體G2 和三體G4函數。

式中，rij是原子i 和j 之間的距離；θijk是以i 原子為中心的j 和k 為鄰居形成的夾角（i、j、k 是原子指數）。GTSD中的關鍵成分是截斷函數fc，它在rc之外衰減到零。高斯型徑向函數和角向三角函數可以通過改變rc、rs、η、ζ 和λ 五個參數來產生一組G2和G4函數，用來區分中心原子i的原子環境。

然而，“exp”自然指數函數的計算速度很大程度上取決于計算機服務器類型，需要專門的計算機指令集來獲得最快的計算速度，如avx512er。通常，冪指數函數的計算速度比自然指數函數快得多。因此，冪指數函數形式的結構描述符（PTSD）被提出來描述原子環境，見式(9)～式(14)[30]。

在PTSD 中，S1 和S2 是二體函數，S3、S4 和S5是三體函數，S6是四體函數。用PTSD中的冪函數代替GTSD中的高斯函數有幾個優點：①減少了數值計算中的計算成本；②將可調參數從兩個（rs,η）減少到一個（n），簡化了對兩體函數最佳參數的搜索；③冪函數與衰減截斷函數的組合可以生成彈性峰形狀和不同的徑向分布。

1.4 SSW-NN

密度泛函理論與勢能面采樣方法（如遺傳算法、盆地跳躍、隨機表面行走SSW 等）的結合已成為解析結構和搜索反應活性位點的有力表征工具。與其他計算方法（如力場、耦合簇）相比，它們在催化方面的成功是由于它們在可接受的計算時間內可以提供可靠的計算結果。可接受的計算時間主要是由于使用了便宜的泛函（如PBE、PW91）和較小的計算模型（＜100個原子）。目前，大多數勢能面搜索的DFT 計算都是在小模型上進行的，這些小模型足以描述簡單的催化系統。對于費托（F-T）催化劑上的長碳鏈生長過程（C＞5）、分子自組裝、無定形結構搜索等復雜體系來講，由于計算時間的限制，DFT無法處理這樣復雜的體系。神經網絡的高效和準確性可大大彌補DFT 的不足，NN 比DFT 至少快3～4 個數量級，同時保持能量和力的精度與DFT 相當。用神經網路勢函數結合勢能面搜索方法來對勢能面結構進行搜索是解決復雜催化體系的強有力的工具。本文作者課題組開發的SSW 和NN（SSW-NN）相結合可以實現對勢能面的快速搜索。完整的SSW-NN 方法的完整使用過程可分為四個步驟：產生DFT數據集、NN 勢能面擬合、SSW-NN勢能面搜索和DFT驗算。

（1）產生DFT 數據集 本步驟的意義在于獲取足夠多的數據集，方便后續NN 訓練使用。在此，根據經驗教訓提出三點注意事項：①訓練集一定要多樣化，包括不同的原子數、不同的化學計量比、不同的原子配位環境（體相、表面、團簇）等；②訓練集的DFT 計算參數一定要采用高精度計算，包括平面波能量截斷、k 點網格密度等；③不同訓練集保證相同的計算參數，方便某些特殊需求時可以便捷地合并訓練集。

（2）NN 勢能面擬合 本步驟的意義在于利用NN 擬合DFT 訓練集得到NN 勢函數。NN 擬合原理及注意事項見上文。表1 列出了常用的NN 擬合過程中的一些超參數。

表1 NN擬合常用超參數

（3）SSW-NN勢能面搜索 本步驟的意義在于利用NN勢函數結合SSW快速搜索勢能面。需要注意的是在進行SSW-NN 之前，一定要對NN 勢函數進行精度分析，確保所得結果準確可靠。此外，由于NN勢函數與DFT所得結果之間存在誤差，可能會導致部分結構能量順序翻轉，這就要求SSW-NN搜索完得到的結果必須要進行DFT驗算。

（4）DFT 驗算 本步驟的意義在于檢驗SSWNN 模擬得到的結果的可靠性。驗算時DFT 的參數設置要求與步驟（1）的訓練集參數設置一樣。另外，驗算時不能只檢查所關心的結構（通常是勢能面極小值），還需驗算與其能量相近的結構，確保沒有發生勢能面極小點預測錯誤的現象。

此外，為了獲得一個穩健可靠、高精度、容錯率高的NN勢函數，在訓練過程中可以通過自學習過程來實現，見圖4。步驟就是上述(1)～(4)過程來回迭代。每得到一次NN 勢函數就進行SSW-NN 搜索，將一些未能學好的結構重新進行DFT 計算添加到原始數據集中，然后再訓練一次產生新的NN勢函數。直到最后產生的NN 勢函數進行SSW-NN模擬時不會有錯誤結果出現。

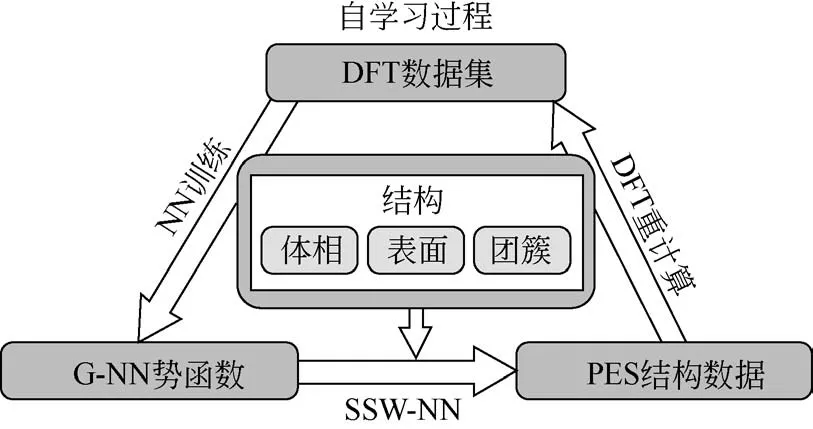
圖4 NN勢函數自學習過程

2 SSW-NN方法應用

2.1 二氧化鈦全局勢能面搜索及結構預測

二氧化鈦（TiO2）半導體材料以其成本低、催化活性高、化學穩定性高、抗氧化能力強、安全無毒以及無二次污染等優點被公認為是最具有開發前景的環保型材料之一[35-37]。迄今為止，研究人員已經發現了十幾種不同的二氧化鈦晶相，從常見的三維晶相（金紅石rutile、銳鈦礦anatase、板鈦礦brookite 等）到二維晶相（纖鐵礦型lepidocrocite-TiO2）。其中，比較獨特的是斜方錳礦型ramsdellite-TiO2（TiO2-R）[38]和錳鋇礦型hollandite-TiO2（TiO2-H）[39]晶相含有一維孔道結構，孔徑在3～5?（1?=0.1nm）。由于Ti4+的可還原性和其便于離子遷移的孔道結構，使得它們已經被開發為鋰（鈉）離子電池的負極材料[40-42]。當然，比TiO2-R和TiO2-H具有更大孔徑的材料也被開發出來了，比如，多孔TiO2膜（平均孔徑約9?）[43-44]、TiO2干凝膠（平均孔徑15?）[45]，但這些孔要么是粒間孔要么是無定形孔，使得這些微孔很容易在高溫下（400oC）坍塌掉。因此，是否存在穩定的、具有更大孔徑的二氧化鈦新晶相仍舊是一個未知之謎。通過對TiO2勢能面進行全局搜索可以回答上述疑問。

采用SSW 方法，從TiO2的不同晶體結構出發[金紅石、銳鈦礦、板鈦礦、TiO2（B）等]，搜索其周圍可能存在的晶相，得到103個勢能面極小點。基于這些勢能面極小點，繪制出了二維TiO2勢能面E-OP 圖，見圖5。其中E 為相對與銳鈦礦的能量，OP 為Steinhardt 類型的有序結構參數（order parameter）。OP可以很好地區分勢能面的結構，具體計算見式(15)。

從圖5(a)中可以看出，整個二氧化鈦的勢能面底部可以看成一個大的“W”。其中常見的金紅石、銳鈦礦、TiO2（B）等均處于“W”底的左半部分（OP=0.3～0.6）。這一部分的典型特征就是所有晶相均是由[TiO6]八面體組成的。而很有意思的是，“W”底的右半部分（OP=0.6～0.9）卻從來沒有人報道過。這右半部分結構的典型特征就是其組成單元為[TiO5]三角雙錐體（trigonal bipyramid，TB）。在這些結構中發現了一系列的微孔TiO2晶體。這些晶體均由[TiO5]三角雙錐體組成。通過不同的組合方式可以形成六元環和八元環微孔，孔徑5.6～6.7?。傳統上一直認為特殊的[TiO5]配位構型是熱力學不穩定的，但DFT-PBE計算結果表明這些TiO2（TB）晶體竟然比常見的金紅石相還要穩定，而且從從頭算分子動力學模擬中也看出這些晶體在高溫下是很穩定的。它們穩定的最關鍵原因是由于Ti-O 晶格中形成的強離子鍵作用，補償了[TiO5]中弱的共價鍵相互作用。通過對鋰離子嵌入能量和結構參數進行評估，預測這些微孔二氧化鈦晶體是良好的鋰離子負極候選材料。

2.2 無定形TiOxHy勢能面搜索及結構預測

二氧化鈦（TiO2）是一種很有前途的光催化劑。然而，受限于寬的帶隙（＞3eV），使得其吸光效率大大降低，只能吸收紫外光。因此，眾多的研究人員試圖通過各種辦法來減小二氧化鈦的帶隙提高催化活性。2011 年，Chen 等[46]取得了重大突破，他們獲得了一種黑色TiO2材料。“黑色”就意味著這個材料在整個可見光區都有很強的吸收能力，并且這個材料表現出很高的催化活性。據報道，黑色TiO2的析氫反應（HER）活性要比普通半導體光催化劑（如商業用P25）的活性高出好幾個數量級[47]。更重要的是，合成黑色TiO2的方法也非常簡單，用含氫的還原劑（如H2和NaBH4）處理原始TiO2材料即可[48-49]。因此，基于Chen 等的結果，后續有大量的研究改變合成條件合成各種各樣的黑色TiO2或者理解為什么黑色TiO2材料可以如此明顯地提高HER 活性。然而，令人遺憾的是，經過這么多年的探索，對機理的理解知之甚少。其中的障礙在于結構的復雜性。大量研究表明，黑色TiO2在加氫過程中涉及復雜的結構演化，伴隨著一系列從TiO2到TiOxHy的相變，導致表面無定形化。在化學和材料科學中，探索無定形表面的結構本身就是一項極具挑戰性的任務，更別提確定催化活性位點。為了解決HER 在無定形表面的活性位點，不僅需要精確的TiOxHy勢能面（PES），而且需要一個強有力的采樣工具能夠遍歷各個可能的結構。因此利用SSW-NN 方法可以實現探索二氧化鈦加氫后無定形殼層的結構，理解結構無定形化機理，從而確定HER 的活性位點。利用SSW-NN，探索TiO2Hx和TiOx的相空間（含有11～16 個原子），氫化的TiO2（112）表面相空間（Ti56O112Hx）。每個配比搜索得到了最少1萬個局域最小值結構，其中包括從晶體結構到非晶結構，定量確定了不同溫度和H2壓力下的TiOxHy結構與組成的熱力學相圖。

圖5 48原子的TiO2全局勢能面等值線圖及TiO2晶體結構

在各種銳鈦礦TiO2表面上，只有在（112）表面上加氫會逐漸導致結構無定形化。如圖6(a)所示，第一層中近乎一半的Ti 原子改變了它們的位置。特別地，25%的Ti5c原子向上隆起，變成了Ti4c原子，另外25%的Ti5c原子向下沉陷到第二層，變成Ti6c原子。在最終重構完的表面上，Ti—O 鍵的長度分布明顯寬化，從1.80?到2.2?，而在未重構的（112）表面為1.9～2.1?。（112）表面完全失去原來的銳鈦礦的鍵合模式，重構成了無定形結構。進一步分析表面H 濃度發現，在H 覆蓋度較低[≤0.19ML（單分子層）]時，（112）表面仍舊可以維持規整的表面結構，所有添加的H原子都位于表面O2c上。H 濃度高于0.19ML 時，表面開始重構，整個重構過程是熱力學有利的。最大放熱發生在表面覆蓋0.69ML 的H 原子，這與未重構表面形成了鮮明對比。未重構TiO2-0.69H 表面的能量要比重構完的TiO2-0.69H 表面能量高3.64eV/(4×2)表面。這種高氫覆蓋的表面不僅使無定形TiO2呈現黑色，而且為HER 反應提供了前所未有的低能壘反應通道：暴露的Ti 原子上可以形成瞬時Ti-H 氫化物。在未重構表面，兩個OH耦合形成H2。由于兩個相鄰的O2cH 之間的距離比較長（初始狀態下的H-H 距離為3.6?），導致反應具有非常高的勢壘2.8eV。而在無定形TiO2-0.69H 表面，存在一條全新的低能壘的反應通道，通過一種全新的TiH/OH耦合機制產H2。與傳統的OH/OH 耦合通道相比（能壘＞1.6eV），TiH/OH耦合反應具有更低的勢壘，即0.6eV[圖6(b)]。電子結構分析表明TiH 氫化物的形成使得電子從高能的Ti 3d 軌道轉移到H 原子上形成H-離子，而H-離子可以很容易地與吸附在O上的H+離子結合形成H2。H-NMR 譜證明在氫化TiO2表面TiH 基團的形成[50]。研究結果不僅對無定形材料特有的表面形態和反應提供了深入的了解，而且證明了利用NN勢函數的全局采樣方法對于解決實際反應下的復雜結構具有廣闊的應用前景。

2.3 ZnCrO 催化劑上的合成氣轉化制甲醇活性位點探索

圖6 無定形TiO2-0.69H表面結構及（112）和無定形表面的H耦合產H2能量曲線

鋅-鉻氧化物（ZnCrO）可被用來催化合成氣轉化制甲醇或其他化學物質[51-52]，并可作為合成氣轉化制烯烴的氧化物-沸石復合催化劑的關鍵成分[53]。作為第一代合成氣制甲醇的工業催化劑[54]，自20 世紀30 年代以來，人們便對ZnCrO 催化劑進行了廣泛的研究。目前普遍認為高溫煅燒后形成的最穩定晶相為尖晶石晶型的ZnCr2O4[55]。許多研究小組已經表明，Zn∶Cr比對合成氣制甲醇的催化活性和選擇性有顯著影響[51,56-59]。當Zn∶Cr比為1∶1時，催化劑通常能達到最佳的活性和選擇性，例如，甲醇的收率約為90g/(kgcat·h)，選擇性為80%[59]。而純ZnCr2O4尖晶石催化劑的活性和選擇性相對較差，甲醇產率小于5g/(kgcat·h)且甲醇選擇性為14%（烷烴的選擇性約為45%）。然而，Zn∶Cr＞1∶2 時ZnCrO結構不確定，目前還沒有關于ZnCrO精確結構的數據。對活性中心的了解不足，阻礙了合成氣在ZnCrO催化劑及相關氧化物分子篩催化體系上催化性能的進一步優化。為了將ZnCrO的原子結構與其催化活性聯系起來，必須探索三元體系的結構空間，并確定與反應條件有關的結構。因此，可以利用SSW-NN 方法來探索ZnxCryOz的結構，從而確定其體相和表面結構。基于SSW-NN方法，每個Zn∶Cr∶O 配比搜索得到最少1 萬個局域最小值結構，其中包括從晶體結構到非晶結構[60]。

圖7 ZnCrO勢能面結構的熱力學結果及其表面的合成氣轉化路線

首先，對體相ZnCrO 結構的熱力學相空間進行掃描，其中Zn∶Cr∶O 比從CrOx延伸到ZnO，見圖7(a)的Zn-Cr-O 三元相圖。尖晶石型晶體結構為ZnCrO 的主要結構框架，范圍從Zn∶Cr=0∶1到Zn∶Cr=1∶1。實驗上已知的ZnCr2O4晶體屬于該區域。這些晶體具有由O2-陰離子形成的面心立方（fcc）子晶格，在間隙四面體（Td）和八面體（Oh）位點具有不同的Zn 和Cr 占據。進一步計算了不同Zn∶Cr比的ZnCrO化合物的形成能并繪制得到熱力學凸圖，見圖7(b)。只有少量的具有尖晶石型骨架的ZnCrO 成分，即Zn3-xCr3+xO8（0≤x≤1）和ZnxCr4O8（1.5≤x＜2），具有負的形成能，表明它們在實驗上有可能被合成出來。體相熱力學結果指出這一范圍內的兩個關鍵組分，即Zn∶Cr=1∶2（原子數比）和1∶1。其中，Zn3Cr3O8晶相中[ZnO6]0h的濃度最高，是Zn∶Cr＞1∶2 化合物的最佳代表。ZnCr2O4中的[CrO6]Oh濃度最高且只有[ZnO4]Td，不含[ZnO6]0h。

進一步的表面結構分析表明，Zn3Cr3O8和ZnCr2O4的最穩定晶面分別是（0001）和（111）晶面。雖然這兩個表面的標記不一樣，但它們顯示出相同的第一層表面結構，即由Zn-O-Cr 相互連接形成的蜂窩狀六元環。其中暴露了三配位的Zn3c、三配位O3c和六配位Cr6c原子[圖7(c)]。而這兩個表面最主要的區別在于第二層的Zn配位。在Zn3Cr3O8中Zn 離子占據了Td和Oh位置，但在ZnCr2O4中Zn離子僅占據Td位置。由于不同的次表層結構導致這兩個表面在反應氣氛下的氧空位濃度不同，Zn3Cr3O8表面不僅在表面可以產生0.25～0.5ML（單分子層）濃度的Ov，而且還可以產生0.25ML 的次表層Ov。而ZnCr2O4的表面Ov濃度在O0v.25ML～O0v.5ML之間。特殊的次表層氧空位導致表面暴露的活性位點完全不同，Zn3Cr3O8表面會暴露兩個采用平面構型的四配位Cr4c原子，而ZnCr2O4表面會暴露出兩個五配位Cr5c原子。

基于以上確定好的表面活性位點，進一步評估ZnCr2O4和Zn3Cr3O8兩種催化劑上的合成氣轉化活性[圖7(d)]。合成氣轉化路徑為：CO—＞CHO—＞CH2O—＞CH3O—＞CH4/CH3OH，反應的決速步為CH3O 加氫。在Zn3Cr3O8表面，產生CH3OH 在動力學上更容易一些，能壘僅為1.33eV。而在Zn3Cr3O8表面，CH3O 加氫更傾向于形成甲烷（反應能壘1.75eV），而非甲醇。產生這種活性差別的本質原因是由于不同的CH3O 吸附：在Zn3Cr3O8表面，弱的CH3O 吸附導致CH3OH 的生成，而ZnCr2O4表面，強的CH3O 吸附則產生CH4。基于以上對催化活性中心的分析，可以很好地解釋為什么Zn:Cr 比變化會極大地影響催化活性和選擇性。

3 結語

本文概述了神經網絡全局勢函數方法及其在多相催化中的應用。從確定反應活性位點到理解反應機理，神經網絡在多相催化領域能夠大放異彩，完全有賴于合理的、多樣和完備的DFT 數據集。未來拓展神經網絡勢函數計算的工作重點之一就是獲取更多的有效數據集，建立數據庫。此外，神經網絡目前主要集中在固體材料的結構搜索，下一步將逐漸構建化學反應勢能面。LASP 軟件中目前提供的反應勢函數覆蓋了Ⅷ過渡金屬和簡單的小分子反應，比如PtCHO（見www.lasphub.com)。考慮到表面反應的復雜性，在此提出幾個未來可能的研究方向。

（1）神經網絡擬合化學反應 該領域面臨的問題是如何獲得足夠多的化學反應過渡態區域的數據集。通常的采樣方法主要集中在勢能面底部，而對于過渡態區域的采樣很少。因此需要有特殊的方法來增強過渡態區域的采樣。

（2）多元素體系的神經網絡擬合 目前HDNN的架構是每種元素有著各自的神經網絡，隨著元素種類的增多，神經網絡的參數會變得很多，訓練及使用過程會變得緩慢，數據集構造也會變得更為復雜，因此需要開發新型的神經網絡架構來滿足多元素體系的使用。

（3）神經網絡擬合其他性質 目前神經網絡主要是獲得結構與能量之間的關系，今后可以擬合其他電子結構數據，如電荷、帶隙等。