非奇異M-矩陣Hadamard積的最小特征值的下界估計

李 華，穆靜靜，李永獻，蘭奇遜

(河南城建學院 數理學院,河南 平頂山 467036)

Cn×n(Rn×n)表示n階復(實)矩陣集, 記Zn為所有非對角元素都為非正數的方陣的集合。設A=(aij)∈Zn如果A=αI-P,其中P>0,α≥ρ(P)則稱矩陣A為M-矩陣.如果α>ρ(P)稱矩陣A為非奇異M-矩陣. 非奇異M-矩陣的集合記為Mn·稱τ(A)=min{|λ|:λ∈σ(A)}為矩陣 的最小特征值, 其中σ(A)為矩陣A的譜集合.

設A∈Mn且不可約, 則存在正向量v使得vA=τ(A)v,稱向量v為A的左Perron特征向量.

先引入以下記號：設A=(aij)∈Rn×n,aii≠0,?i,j,k∈N,j≠i,t=1,2,…,

設A=(aij),B=(bji)∈Cn×n，稱矩陣C=A。B=(cij)=aijbij為矩陣A與B的Hadamard積.

由文獻[1]知, 如果A和B都是M-矩陣, 則B。A-1也是M-矩陣. 若A∈Mn則存在一個正對角矩陣D,使得D-1AD是行嚴格對角占優的M-矩陣.

設A=(aij),B=(bij)∈Mn,A-1=(aij),對于τ(B。A-1)的估計，有如下結果：

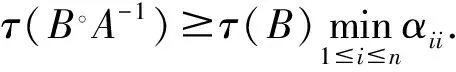
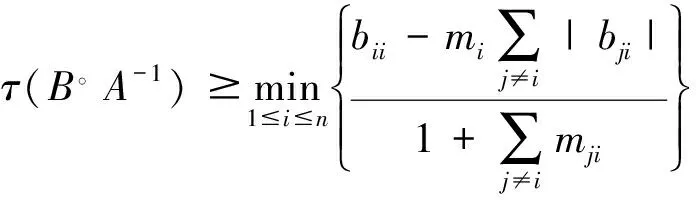
2017年趙建興等[5]得到：

本文繼續對非奇異M-矩陣B和非奇異M-矩陣A的逆矩陣A-1的Hadamard積的最小特征值進行估計，得到τ(B。A-1)的單調遞增收斂的下界序列，且新的估計式改進了文獻[3-5]的相應結果.

1 非奇異M-矩陣研究的主要結果

引理1[1]設A,B∈Rn×n,D,E為兩個正對角矩陣, 則有

D(A。B)E=(DAE)。B=(DA)。(BE)=(AE)。(DB)=A。(DBE)

引理2[6]設A=(aij)∈Cn×n,xi>0,i=1,…n,則矩陣A的所有特征值位于下列區域的并集中:

引理 3[2]設A=(aij)∈Cn×n,xi>0,i=1,…n,則矩陣A的所有特征值位于下列區域的并集中:

引理 4[5]設A=(aij)是行嚴格對角占優的矩陣, 則?i,j∈N,j≠i,t=1,2,…,有

定理1 設矩陣A=(aij),B=(bij)∈Mn,A-1=(αij),則對任意的t=1,2,…,有

證明：當n=1時, 顯然成立，假設n≥2.

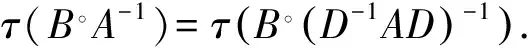
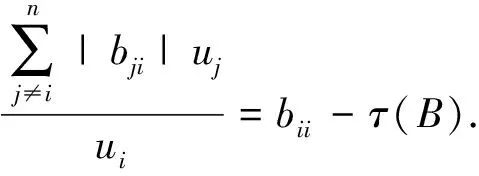
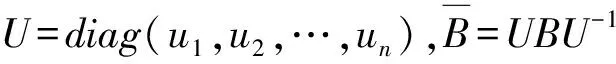
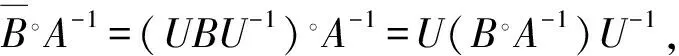
則有：

若A和B中至少有一個是可約矩陣,設D=(dij)為置換矩陣, 其中d12=d23=…dn-1,n=dn1=1,其余的dij=0,則對任何正實數t,A-tD,B-tD的所有順序主子式是正的,從而A-tD,B-tD為非奇異不可約M-矩陣,用A-tD,B-tD分別代替A,B, 讓t→0由于連續性, 則可得到上述同樣的結果.

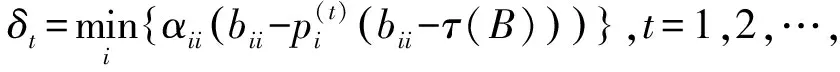
定理2 序列{δt}是單調遞增且有上界的序列，因此是收斂的.

定理3 設矩陣A=(aij),B=(bij)∈Mn,A-1=(αij),則對任意的t=1,2,…,有

證明：當n=1時, 顯然成立.假設n≥2.

由于A∈Mn,則存在正對角矩陣D,使得D-1AD為行嚴格對角占優的 矩陣.由于D-1(B。A-1)……