基于有限元的軸孔過盈配合接觸應力影響因素研究

王勝曼

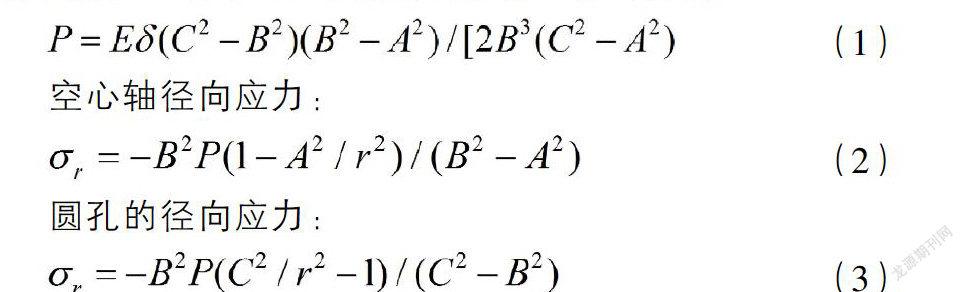
摘要：軸孔過盈配合是機械工程中一種重要的定位和連接方式。本文針對軸孔過盈配合結合面上應力分布問題，利用UGNX有限元仿真軟件，基于彈性力學孔口應力集中理論，從軸孔結合長度、軸孔過盈量、軸孔徑向尺寸以及軸孔材料特性等四個維度對接合面上的接觸應力分布進行了有限元分析。結果表明結合應力大小與過盈量、徑向尺寸以及材料特性有關，而與軸孔配合長度無關，仿真結果與研究理論相符。同時還發現應力集中沿軸向分布區域不隨軸孔結合長度、過盈量大小、徑向尺寸以及材料特性的變化而變化。此研究結論為軸孔過盈配合過盈量的合理選擇，軸孔結構尺寸的設計和疲勞強度計算等提供了理論參考。

關鍵詞：軸孔過盈配合;接觸應力;應力集中;有限元;影響因素

0? 引言

軸孔過盈配合是機械零部件聯接的主要方式之一。采用軸孔過盈配合進行聯結，可以使軸孔兩個零件配合精度高，對心精度好，而且加工制作簡單，成本較低。因此軸孔過盈配合這種連接方式在機械裝配部件中得到了廣泛的應用，如軸轂聯接、軸承內圈與軸的配合、軸承外圈與箱體座孔的配合、銷軸與耳環的配合、活塞與活塞銷的配合等等。由于過盈量的存在，使得軸孔結合面上出現情況較為復雜的接觸應力，在軸孔的接觸邊緣出現應力集中現象。接觸應力直接影響軸孔聯接的可靠性以及疲勞壽命。因此研究軸孔過盈配合接觸應力的影響因素是本課題研究的重點內容。

在工程實際問題中，軸孔結合面上接觸應力又受到軸孔幾何尺寸、過盈量大小、表面粗糙度、軸孔材料等多種因素的影響。一些學者關于軸孔過盈配合結合面上出現的應力做了一些研究，理論都基于彈性力學中有關孔應力的計算與分析，得出了應力在徑向分布的解析解，并結合有限元分析方法做了一些簡單數值解驗證[1-6]。但是還沒有對于接觸應力問題從多個影響因素進行系統地有限元分析。對于軸孔配合面上應力沿軸線分布狀態與哪些因素相關也還沒有進行深入研究與計算。本課題利用有限元分析方法，采有UGNX研究工具，在一定的假設條件下，建立軸孔過盈配合模型，分別從軸孔結合長度、軸孔之間的過盈量、軸孔徑向幾何尺寸、軸孔材料特性等四方面因素對接觸應力分布及軸向應力集中分布區域進行研究。通過比較分析得出了孔口徑向應力集中與過盈量、徑向幾何尺寸以及材料特性有關。過盈量越大，應力集中現象越明顯;徑向尺寸越小，應力集中越不明顯;彈性模量越大，應力集中越大。軸向應力集中分布區域與軸孔結合長度、過盈量和徑向尺寸沒有直接關系。此結論為機械工程中采用軸孔過盈連接的機械零部件設計的強度校核和疲勞壽命計算提供了依據，同時也為軸孔過盈配合減輕應力集中現象提供了理論依據。

1? 研究理論[7]

根據彈性力學理論，對于空心軸軸孔過盈配合，按圓筒受壓的軸對稱問題，根據過盈量和軸孔配合變形協調方程，可以求出空心軸和圓孔所受的徑向壓力為：

通過以上三個公式可以看出，徑向接觸應力與材料的彈性模量、過盈量以及軸孔的徑向尺寸有關。

2? 軸孔過盈配合材料特性與結構尺寸

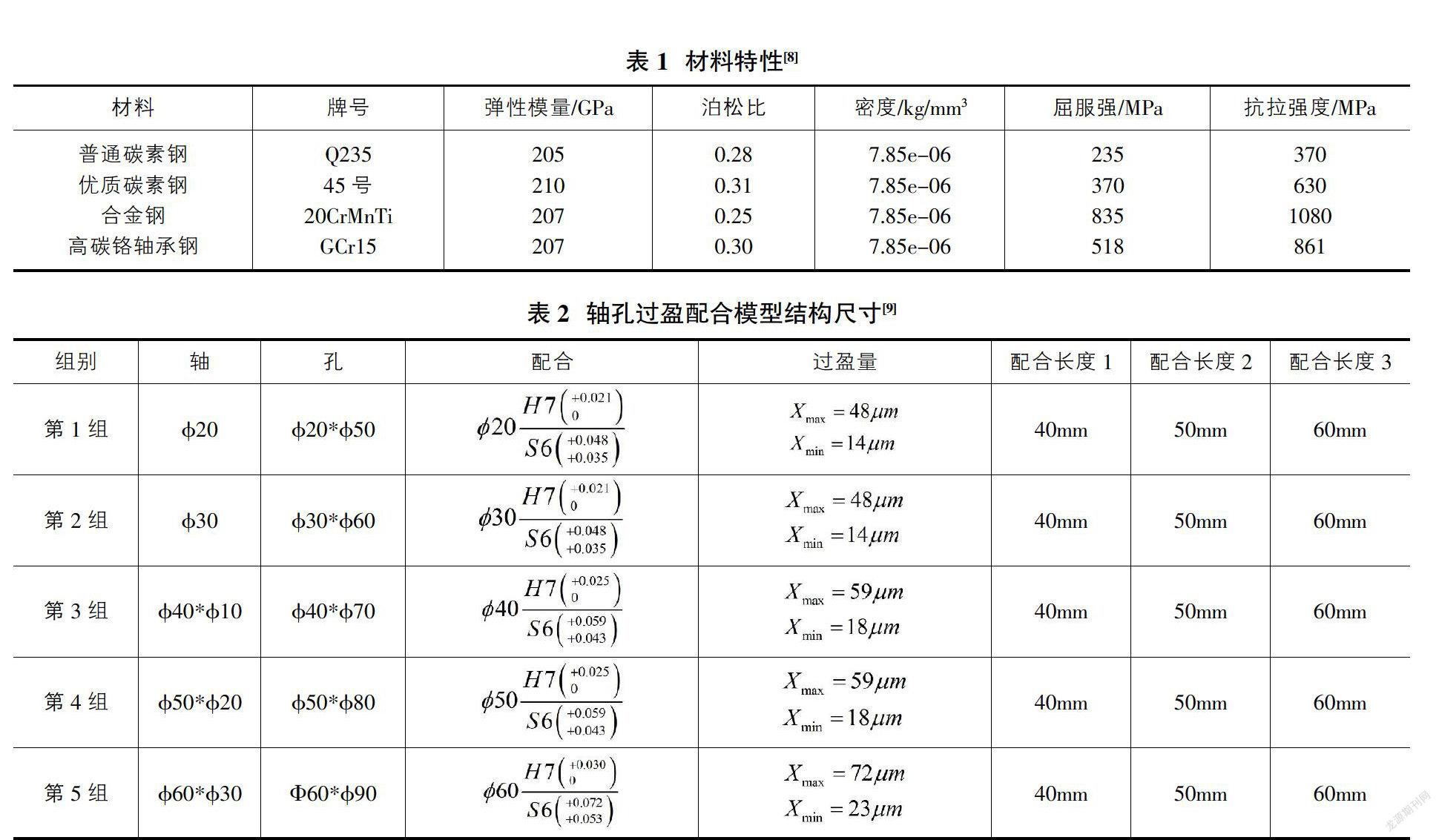
為了使研究更加接近于實際工程中的軸孔過盈配合問題，本研究根據實際工程中軸孔常用材料和一般軸孔配合尺寸進行模型簡化。常用材料特性如表1所示，軸孔簡化模型尺寸如表2所示。

軸孔過盈配合模型有限元分析是在不考慮表面粗糙度、形位誤差的影響下，應力處于軸對稱平面應力狀態，應變均在彈性范圍內，進行的線性有限元分析。

3? 軸孔過盈配合有限元仿真模型的建立[10]

根據表1中提供的軸孔材料特性和表2中提供的軸孔幾何尺寸，在UGNX中分別對其進行三維建模，利用接觸和對齊命令進行軸孔裝配，裝配完成后導入高級仿真環境，進行有限元模型的建立。分別進行材料屬性的設置，物理屬性的創建以及網格的劃分，每組網格化分等級相同。完成有限元模型后再創建仿真模型，約束采用固定約束，空心軸約束內孔表面，孔約束左右兩側面。仿真對象類型采用面對面接觸，接觸算法采用罰函數法。求解器采用NX NASTRAN，分析類型采用線性靜力學分析。求解前的仿真模型如圖1所示。

4? 軸孔過盈配合仿真結果分析

4.1 軸孔結合長度對接觸應力的影響[11]

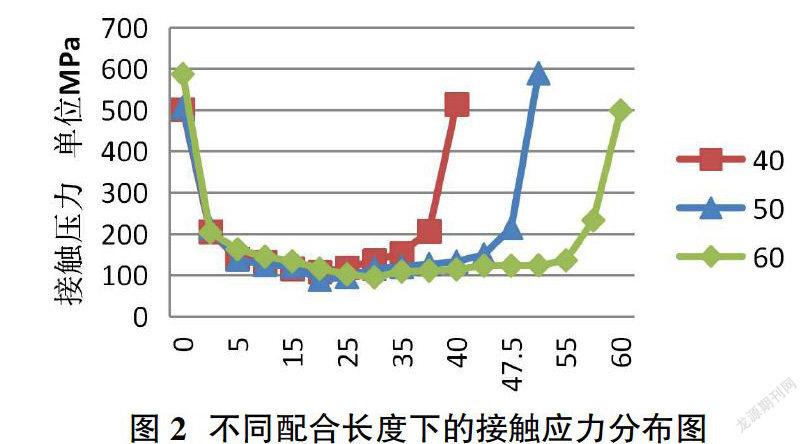
為了研究軸向尺寸對接觸應力的影響，主要選取了表2 中的第1組數據，三種長度的軸孔配合，分別是40mm、50mm、60mm，三組分別按最大過盈量0.048mm進行仿真實驗，得到三組接觸應力云圖。在此基礎上并沿軸線方向創建接觸路徑，生成了接觸應力沿軸向方向分布圖。這說明在材料特性、徑向結構尺寸以及過盈量等相同的情況下，只改變軸向結合長度。仿真分析結果從圖2中可以看出：①三組長度的配合，在結合邊緣都出現了應力集中現象，并且應力集中沿軸向方向的發生區域大致相同，約是2.5mm。這說明結合長度并不影響應力集中在軸向方向的發生區域。②結合面上的應力分布狀態三組的趨勢基本相同，都是從距左右兩端2.5mm向內開始，應力數值逐漸向中心區域變小。在軸孔結合的中間部位，結合面上的應力最小。而且三組示例結合面上的應力均值非常接近，沒有較大的差異性。這說明結合長度的改變，不會改變結合面上應力分布的趨勢和應力數值。

4.2 過盈量對接觸應力的影響[12]

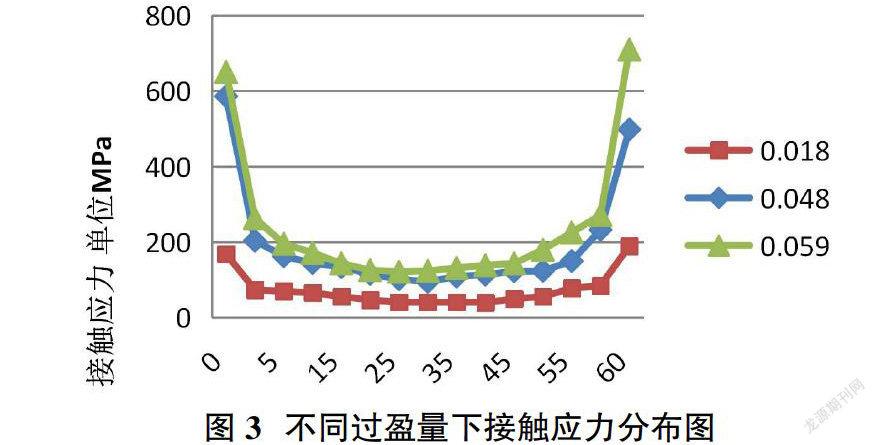
利用有限元分別對三組不同過盈量的軸孔過盈配合進行仿真實驗。為了研究過盈量對結合面應力的影響，以表2中的第3組軸孔結構尺寸為例，過盈量分別選取了最小過盈量0.018mm、最大過盈量0.059mm和中間過盈量0.048mm，三種情況進行應力分析和邊緣應力集中現象分析，得到接觸應力云圖。在此基礎上并沿軸線方向創建接觸路徑，生成了應力沿軸向方向分布圖3所示。從圖3中我們可以發現：

①過盈量越大結合面上的接觸應力就越大，接觸應力與過盈量呈正比關系。

②三種過盈量下的軸孔兩端的應力集中區域非常接近，兩端均約2.5mm。這說明過盈的大小不能改變應力集中沿軸線方向的區域。

③徑向應力集中與過盈量有關，過盈量越大，徑向應力集中數值越大。仿真結果是：過盈量為0.059mm的應力集中最大數值>過盈量為0.048mm的應力集中最大數值>過盈量為0.018mm的應力集中最大數值。

4.3 徑向尺寸對應力的影響

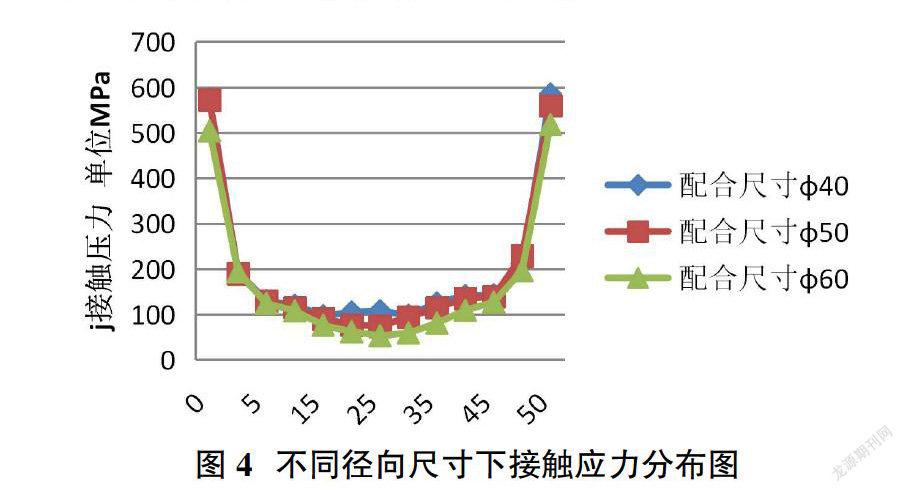
在過盈量、材料特性、軸向結構尺寸相同的情況下，改變軸孔過盈配合的徑向尺寸大小。分別選取表2中的第3組、第4組和第5組數據分別進行仿真。從仿真分析結果來看如圖4所示：①軸孔配合尺寸為？準40mm時，接合面上的應力最大，軸孔配合尺寸為？準60mm時，接合面上的應力最小，軸孔配合尺寸為？準50mm時，接合面上的應力居于中間值。這說明軸孔徑向尺寸越小，接合面上的應力越大，軸孔徑向尺寸越大，接合面上應力值越小。徑向尺寸是影響接合面徑向應力大小的重要參數。②在不同的配合尺寸下，應力集中沿軸線發生的區域基本相同，這說明徑向尺寸大小不改變應力集中發生的區域。

4.4 材料特性對接觸應力的影響

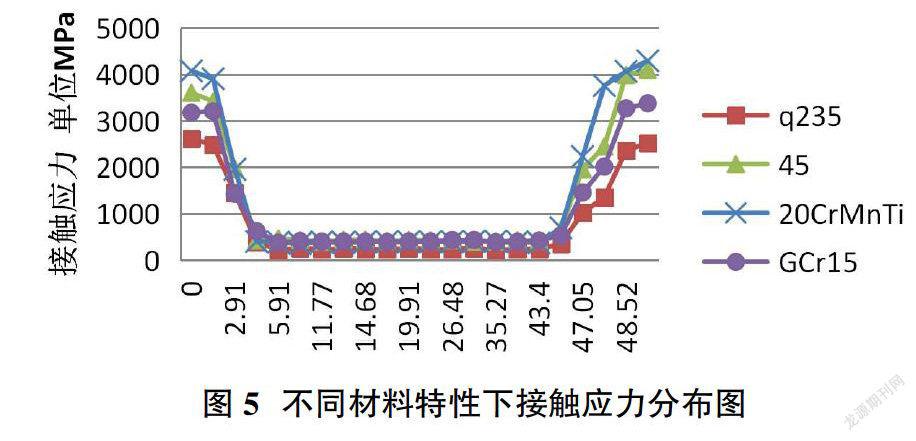
軸孔過盈配合中軸和孔常用的材料有優質碳素鋼45號鋼、合金鋼20CrMnTi、滾動軸承用鋼GCr15和普通碳素鋼Q235等，材料特性特性如表1所示。為了研究材料特性對軸孔過盈配合結合面上應力的影響，軸孔結構尺寸選取表2種的第2組數據，結合長度為50mm。軸孔采用相同的材料，四組分別選取表1中的四種材料進行仿真實驗。

在軸孔結構尺寸相同的情況下，從圖5中比較四組仿真結果可以發現：①四種材料的軸孔裝配后，應力集中發生的區域沿軸向方向非常接近，兩端應力集中的區域距孔口或軸段向內分別是約2.95mm。四種材料的應力集中沿軸線方向的區域沒有顯著差異，這說明應力集中沿軸線分布區域對材料的特性不敏感。②從圖5中可以看到，四種材料的單元-徑向應力集中的數值大小呈現一定的差異，其中20CrMnTi材料的單元-徑向應力集中數值較大，Q235材料的單元-徑向應力集中數值相對較小。這說明徑向應力集中與材料特性有一定的關聯，因四種材料都是機械工程中常用金屬材料，而且材料的彈性模量和泊松比比較接近，因此徑向應力的差異性比較小。③在過盈量相同的情況下，四種材料的軸孔結合面上的應力沿軸線方向（除去兩端應力集中部位）非常接近，但仍有一些小的差異。這說明材料特性對于接合面上的應力有一定的影響。根據前面理論公式1可知，結合面上的應力與彈性模量和過盈量成正比，因四組軸孔配合的過盈量相同，材料彈性模量E比較接近，因此仿真結果與理論分析基本相同。

5? 結論

本文利用有限元分析方法對軸孔過盈配合接觸應力問題，從結合長度、過盈量、徑向幾何尺寸以及材料特性等四個維度進行了有限元仿真，對分析結果進行總結得出如下結論：

①軸孔材料、過盈量和徑向尺寸相同的情況下，改變軸孔結合長度，左右邊緣出現的應力集中在軸向分布區域約為距離左右端面向內2.5mm，三組數據非常接近。因此軸孔過盈配合結合長度對左右邊緣應力集中的軸向分布沒有顯著影響。

②軸孔材料、結合長度、徑向尺寸相同的情況下，改變過盈量，導致左右邊緣徑向應力集中數值增大，但不影響應力集中在軸線方向的分布區域，分布區域約為距離左右端面向內2.5mm。因此過盈量大小，只改變了徑向應力值而未改變軸向方向應力集中的分布區域。

③軸孔材料、過盈量、軸向結合尺寸相同的情況下，改變軸孔結合的徑向尺寸，會導致應力集中數值發生變化。軸孔結合面徑向尺寸越大，應力集中數值越小;反之數值越大。但是徑向尺寸的改變，并不影響應力集中沿軸線方向分布的區域，分布區域約為距離左右端面向內2.5mm。因此徑向尺寸改變影響了徑向應力集中數值，但不影響軸向方向應力集中的分布區域。

④軸孔結合長度、徑向尺寸、過盈量等因素相同的情況下，改變軸孔材料特性，接觸應力會發生變化，彈性模量E越大，接觸應力越大，反之數值越小。材料特性的變化不改變軸向應力集中發生的區域變化。

⑤利用有限元分析可以更加真實的反應結合面上的應力分布狀態，沿軸線方向是中間區域應力較大，應力值逐漸向兩端變小。而理論公式求解的是接合面上的平均值，即在整個結合長度上，結合面上的應力值是同一值。如果進行精確研究，選擇利用有限元數值解的計算方法相對較好。

參考文獻：

[1]李兵.回轉窯拖輪與軸受強壓時過盈配合的ANSYS分析[J].水泥工程，2004，2：44-52.

[2]李毅.基于ABAQUS的過盈配合有限元數值仿真[J].制造業自動化，2012，4：148-150.

[3]王國榮.空氣錘釬頭齒孔過盈配合數值模擬研究[J].石油機械，2010，4：30-34.

[4]郭愛貴.基于有限元法的過盈配合接觸特性分析[J].成組技術與生產現代化，2009，26（4）.

[5]楊新平.表面形狀誤差對過盈配合性能的影響及其計算研究[D].西北農林科技大學，2003.

[6]陳家兌.過盈聯接的有限元模擬[J].兵工自動化，2007，26（5）：51，59.

[7]徐芝綸.彈性力學[M].北京：高等教育出版社，2016，03.

[8]成大先.機械設計手冊[M].六版.化學工業出版社，2016，04.

[9]武文革.互換性與測量技術基礎[M].二版.電子工業出版社，16-34.

[10]沈春根.UGNX有限元分析入門與實例精講[M].二版.機械工業出版社，2016，05.

[11]郭鵬程.配合長度對配合性質的影響[J].機械工程師2013，1：66-67.

[12]魏延剛.軸轂過盈聯接的應力分析和接觸邊緣效應[J].機械設計，2014，1：36-39.