關于“阿氏圓”模型的探究與思考

施德儀

[摘? 要] “挖掘教材價值，總結模型”是當下數學教學所倡導的一種模式. 在教學中需要有意識地引入一些常用的數學模型，利用模型探究來深化知識理解，發展數學思維. 文章主要探究初中數學重要的幾何模型——“阿氏圓”模型.

[關鍵詞] “阿氏圓”;模型;解讀;應用;拋物線;思考

模型背景

“PA+k·PB”型是初中數學常見的最值類型之一，當k=1時，即可轉化為常見的“飲馬問題”模型來求解;而當k為不等于1的正數時，則需要變化思路來加以研究，一般有兩種情形：一是點P在直線上運動，則為經典的“胡不歸”問題;二是點P在圓周上運動，則為“阿氏圓”問題，即已知平面上有A，B兩點，則所有滿足PA+k·PB （k≠1）的點P的軌跡為一個圓. 由于其最早是由阿波羅尼斯發現的，故又稱為“阿波羅尼斯圓”. 利用“阿氏圓”模型的結論及策略，有助于問題思路的構建，適度拓展模型，有利于解析綜合性問題.

構建解讀

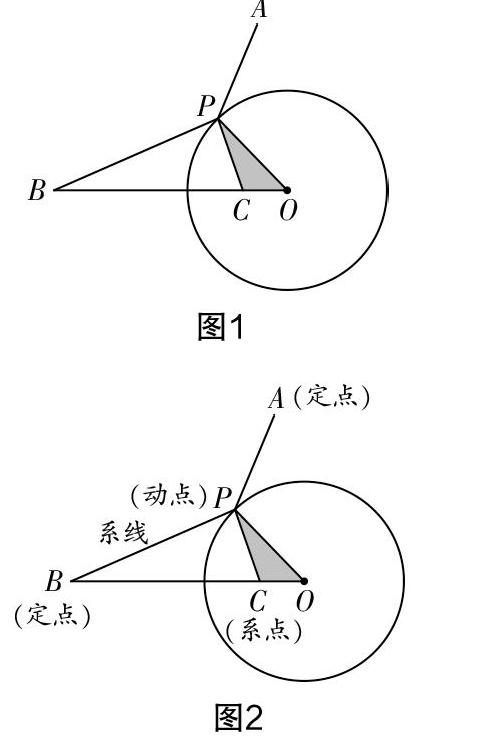
如圖1，⊙O的半徑為r，點A和點B都在圓外，點P為⊙O上一個動點，已知r=k·OB，連接PA和PB，試分析“PA+k·PB”取得最小值時，點P的位置.

上題突破的關鍵是處理“k·PB”的大小. 若在線段OB上截取OC，使得OC=k·r，則可以確定△BPO與△PCO相似，從而有k·PB=PC. 后續則可轉化為研究“PA+PC”的最小值，其中點A和點C為定點，點P為動點，顯然可以直接利用共線原理來求最值.

深入探究其圖像，由逆向思維可將“阿氏圓”模型視為“母子型相似+兩點間線段最短”. 點P在⊙O上運動時，A，B為定點，PA和PB不斷變化，解決該問題時首先需要合理構造母子型相似三角形，利用其性質來轉化問題，即在OB上找到一點C，使得■=■=k，此時便有△BPO∽△PCO.

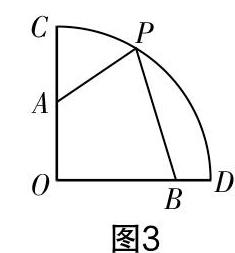
而在實際解析時需要明晰問題模型，因此把握模型的結構尤為重要. 以圖2“阿氏圓”模型圖像為例，其中點A和點B為定點，點P為動點，變直線BP為系線，突破的關鍵是確定系點C，從而確保其中的“母子”三角形相似，即△BPO∽△PCO.

解題策略

從突破過程來看，共分為兩個階段：一是確定系點，構建相似三角形;二是利用“兩點之間，線段最短”原理，分析三點共線情形，完成動點位置確定. 具體解題時可以按照如下策略及步驟進行：

第一步，連接動點與圓心、定點與圓心，如上述所構建的模型，連接OB和OP;

第二步，計算■，確定線段比為k的情形，如上述模型中的■=k;

第三步，在線段OB上確定系點C，構造相似三角形，由相似性質提取線段比例關系，如上述模型中的■=■.

典例講評

上述對“阿氏圓”模型進行了詳細解讀及解析策略探究，但針對不同的問題情形需要具體分析，要學會準確識別模型，添加輔助線. 下面結合例題探究解析過程.

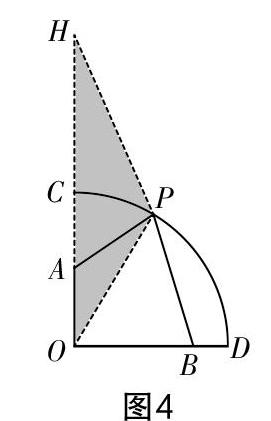
例題 如圖3，在扇形COD中，∠COD=90°，OC=6，點A在OC上，OA=3，點B在OD上，OB=5，點P是■上的一個動點，試求2PA+PB的最小值.

分析 要求2PA+PB的最小值，其中k≠1，且點P為圓弧上的一個動點，顯然屬于“阿氏圓”問題模型. 因此解析的關鍵是尋找線段比與k相關的情形，確定系點的位置.

解答？搖 連接OP，其中k=2，因為OC=6，OA=3，OB=5，所以■=■，■=■. 可將■=■視為■=■，因此可在OA延長線上取一點H，使得OH=2OP=12（如圖4）. 此時就有■=■=■，又∠AOP=∠POH，所以無論點P如何移動，始終有△PAO∽△HPO. 由相似性質可得PH=2PA，所以2PA+PB=PH+PB，其中點H和點B為定點，顯然當H，P，B三點共線時，PH+PB取得最小值，且最小值為BH=■=13，即2PA+PB的最小值為13.

評析？搖 上述解析過程把握圖像結構及k值大小，從而確定了“阿氏圓”模型，在此基礎上分析線段比值，確定系點位置. 對于“阿氏圓”模型，剖析的關鍵是深刻理解探究系點實則是通過構建相似三角形將其轉化為常規的線段和問題，而在實際轉化時需要把握圖像特點，合理利用圓的性質條件.

拓展探究

“阿氏圓”模型可視為常規的平面幾何問題，而函數與幾何的融合是近幾年中考的命題趨勢，對于“阿氏圓”模型同樣也不例外. 近幾年中考及模擬考試題中出現了一些以拋物線為背景融“阿氏圓”模型的考題. 對于該類試題，除了需要合理按照模型突破的方法和步驟解析外，還需要充分利用平面直角坐標系中點的坐標與線段長的關聯，以及拋物線的性質，才能順利解題. 下面以一道考題為例，詳細探究解題細節.

考題 如圖5，已知拋物線的解析式為y=-x2+bx+c，拋物線與直線AB交于點A（-4，-4）和B（0，4），直線AC的解析式為y=-■x-6，直線AC與y軸交于點C. 點E是直線AB上的一個動點，過點E作x軸的垂線，延長垂線與AC交于點F，與拋物線交于點G.

（1）求拋物線的解析式.

（2）連接GB，EO，若四邊形GEOB為平行四邊形，試求點G的坐標.

（3）①y軸上有一點H，連接EH和HF，試分析點E運動到何位置時，四邊形AEFH為矩形，并求出點E和點H的坐標;

②在①成立的前提下，以點E為圓心、EH的長為半徑作圓，點M為圓上的一個動點，試求■AM+CM的最小值.

解析 容易求得拋物線的解析式為y=-x2-2x+4. 在此主要分析（3）問的第②小問，由（3）①問可知以下點的坐標：E（-2，0），H（0，-1）. 又A（-4，-4），所以EH=■，AE=2■. 如圖6，設AE與⊙E交于點N，取EN的中點P，則點N的坐標為（-3，-2），點P的坐標為-■，-1，PE=■. 連接PC與⊙E的交點即為■AM+CM取得最小值時點M的位置，點P為“阿氏圓”模型的系點，具體原因如下.

因為EM=EH=■，顯然■=■，■=■，所以△PEM∽△MEA. 根據相似性質可得PM=■AM，從而有■AM+CM=PM+CM. 因為點P和點C為定點，點M為動點，由“兩點之間，線段最短”可知，當P，M，C三點共線時，PM+CM取得最小值，此時PM+CM=PC. 由上述信息可求得PC=■，所以■AM+CM的最小值為■.

評析？搖 上述第（3）②問的問題模型實則就是初中常見的“阿氏圓”模型，顯然突破的關鍵就是確定模型中的“系點”. 可利用相似比將其轉化為常規的線段和問題，即“■AM+CM→PM+CM”，然后利用三點共線確定線段和的最小值. 與純幾何模型問題相比，融合拋物線的“阿氏圓”模型更注重對點坐標橋梁作用的利用，即可用點的坐標推導線段長、推理線段比，這些內容是后續挖掘三角形相似的關鍵.

教學思考

“阿氏圓”模型的解析思路可為求解含參線段和最值問題提供參考，有利于學生認識圖形結構，打開解題突破口. 下面提出幾點教學建議.

1. 深度挖掘模型，理解突破本質

“阿氏圓”模型是隱含在數學教材中的經典模型，深入探究模型結構、總結破解方法有助于整合教材資源，強化學生對教材定理、模型的理解. “阿氏圓”模型是基于圓的性質、母子型相似模型和兩點之間線段最短定理所構建的一種特殊的動點最值模型，教學時需要引導學生關注模型特點，挖掘模型結構，把握模型條件，歸納模型結論，同時引導學生體驗模型解析的構建過程，把握模型相似變換的數學本質，形成對模型的深刻認識.

2. 適度延伸拓展，強化數學思維

數學的思維方式是數學教學的重點，在“阿氏圓”模型的探究及應用過程中，學生對相似變換和共線定理有了更為深刻的領悟，能夠準確地辨析模型，理解模型，用模型的特征規律來探究問題. 實際上，“阿氏圓”模型并不是一個單純的幾何模型，而是眾多數學定理、定義、規律、方法的融合，對其適度拓展可形成新的問題模型. 例如，上述基于平面直角坐標系將其與拋物線相關聯，形成了函數與幾何背景下的“阿氏圓”模型，這也是中考命題的新趨勢. 因此，探究模型時，需要基于知識關聯拓展延伸，引導學生聯系拋物線的性質特征來挖掘“阿氏圓”，形成新問題的解析策略，拓展學生的思維方式.

3. 滲透思想方法，提升核心素養

“阿氏圓”模型的突破，實則是相似轉化的過程. 在該過程中，通過截取線段、構建相似模型，能將含參線段和問題轉化為一般的線段和問題，其中運用了數學的轉化思想和模型思想. 開展“阿氏圓”模型探究，不僅應關注模型的解析思路，還應立足模型的突破思想，從思想層面理解模型的本質及意義，這也是初中數學模型探究教學的重要任務. 因此，在模型探究時，應合理滲透數學的轉化思想和模型思想，引導學生理解數學思想的內涵，深刻體會思想方法解析問題的過程，領悟思想與知識之間密不可分的關系，逐步提升學生的核心素養.