面向樓梯應急通信系統的隨機多簇信道模型

梁金鵬，李正權

江南大學 江蘇省模式識別與計算智能工程實驗室，江蘇 無錫 214122

1 引言

樓梯在緊急情況（如火災和地震）發生時具有重要作用[1]。在樓梯應急通信系統的設計中，其物理層算法的選擇主要取決于對室內樓梯信道傳播特性的全面了解[2-4]。

室內樓梯無線信號傳播特性的研究最早可追溯到20 世紀90 年代[5]。隨后幾十年中，室內樓梯信道模型一直受到持續關注。一般而言，這些信道模型可以分為三種不同類型。第一種是確定性模型[6-8]。在這些模型中，信道參數如路徑損耗可以通過射線追蹤技術來估計。第二種是統計性模型[9]。一些常見分布例如Rayleigh、Rice、Nakagami 等，被用于描述樓梯環境下的信道統計特性。第三種是半確定半統計模型。這種模型將幾何光學與統計學相結合來對無線信道傳播特性建模。

總而言之，這些模型都擁有同一種特性，即它們都關注于對樓梯環境下的路徑損耗特性建模。但以上研究都未考慮信道沖擊響應（Channel Impulse Response，CIR）。CIR 為通信系統的設計提供了重要的參數信息[10]。然而信號在密集反射和散射環境下會以簇的形式到達接收端，導致CIR 建模難度加大。此外，多簇特性對信道容量也具有重要影響[11]。最早描述信號多簇特性的是S-V模型[12]，該模型將簇和簇內多徑分量的到達時間描述為雙泊松到達過程，但S-V模型并未考慮樓梯環境。樓梯是一種特殊的周期性結構[6]，其傳播特性與其他室內環境不同，因而無法通過S-V模型確定簇的到達時間。

為有效且準確描述樓梯信道多簇特性，本文提出了一種新的隨機多簇信道沖擊響應模型。在視距（Line of Sight，LOS）和非視距（Non LOS，NLOS）兩種不同的傳播環境下，理論分析了每個簇的形成以及簇到達時間與收發天線距離的關系，并給出理論與實測數據的仿真結果。此外，還提出用距離相關的線性函數來描述每個簇的功率衰減常量。最后通過信道測量實驗、平均功率時延譜（Average Power Delay Profile，APDP）和均方根（Root Mean Square，RMS）時延擴展來檢驗所提出模型的準確度。并與經典的S-V模型進行客觀比較，表明所提出模型更適合描述室內樓梯無線傳播特性。

2 信道測量

2.1 樓梯環境

本文在幾個樓梯環境下展開信道測量實驗，它們皆位于同一棟典型辦公大樓。樓梯環境的示意圖如圖1所示[13]。其中，樓梯臺階和周遭墻壁均為混泥土構成，樓梯扶手為鋼筋材料。每個臺階長1.20 m，寬0.28 m，高0.15 m。值得注意的是，在上行樓梯的第二個臺階上方2 m高處有一根混凝土橫梁。

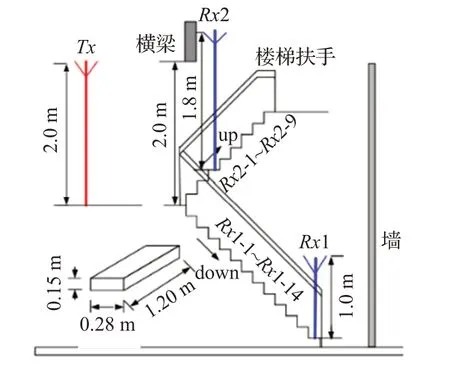
圖1 室內樓梯測量環境

2.2 測量系統

關于測量系統的詳細描述可參考文獻[13]。該測量系統以矢量網絡分析儀（Vector Network Analyzer，VNA）為核心，生成2.50～2.69 GHz 的掃頻信號，共記201 個掃頻點。將復數頻率響應進行逆傅里葉變換后得到CIR。其中，CIR 的分辨率為5.26 ns。在實驗分析中，將CIR 的觀察時延窗口截取為100 ns，最終得到20個時延bin[14]。

2.3 測量計劃

在整個信道測量實驗中，發射天線（Tx）固定不動，接收天線（Rx1）沿臺階移動。其中，Tx和Rx1 的高度分別為2.0 m和1.0 m。如圖1所示，Tx和臺階1（Rx1-1）之間的距離為2.0 m。測量實驗包含LOS 和NLOS 兩種情形。LOS 實驗在下行樓梯的14 個臺階（Rx1-1～Rx1-14）上進行，而NLOS則從上行樓梯的第4個臺階（Rx2-4）開始，到第9個臺階（Rx2-9）結束。在所有實驗中，由于周圍沒有人員移動，測量的信道可以被認為是時不變的。

3 提出的隨機多簇信道模型

在室內無線傳播中，由于反射路徑上障礙物尺寸較大，多徑分量往往以成簇形式到達接收端[15]。在本文中，CIR建模的關鍵是首先確定簇到達時間。

3.1 簇到達時間

根據文獻[16]，室內樓梯環境下的CIR 可以用頻域自回歸模型來描述。其中，在觀察時延窗口內，存在三個明顯的自回歸傳遞函數極點，而每個極點可以看成時域中重要的到達簇[17]。因此，結合樓梯結構和電磁波理論，假設時域上存在三個到達簇。第一簇的形成和收發天線周圍的直射和反射信號有關，其到達時延(T1)可用式（1）中距離相關的線性函數表示。

第二簇由從樓梯左側墻壁反射而來的多徑分量組成。第三簇為高階反射簇，其至少經歷了兩次反射，因此傳播時延相對前兩簇較高。在式（2）和式（3）中，采用不同的線性函數描述第二和第三簇的到達時延（T2和T3）與收發天線距離之間的關系。此外，這兩個反射簇各自的陰影效應分別用零均值的正態分布變量Dω、Dσ表示[18]。

綜上所述，給出了T1、T2和T3與收發天線距離d之間的線性關系，其各自表達式分別如下：

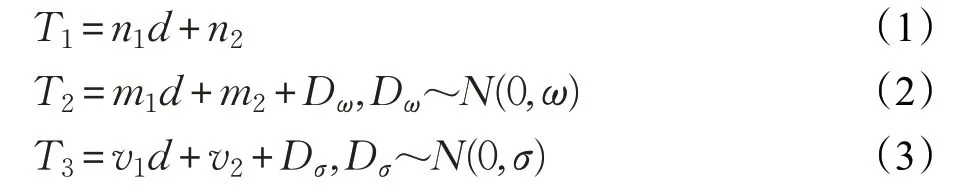
其中，n1,n2,m1,m2,v1,v2為擬合函數的參數。ω和σ為正態分布變量的標準差。

隨后將時域時延軸用bin表示，每個簇時延bin的數量計算如下，其中R(?)表示將到達時間四舍五入到最近的整數，Δτ為時域分辨率：

3.2 功率歸一化和衰減常量

在CIR建模之前，需要用路徑損耗(PL)將CIR每個時延bin上的功率歸一化。路徑損耗通常被建模為一個對數正態分布的隨機變量，其均值為距離相關的函數[19]。

在多簇信號中，簇內多徑分量功率一般隨時延指數衰減[12]。根據文獻[20]，每個簇的衰減常量不同并可表示為時延相關的線性函數。從測得的樓梯功率時延譜（Power Delay Profile，PDP）中，得到與文獻[20]類似的觀察結果。不同的是，將衰減常量與環境信息聯系起來，將每個簇的衰減常量(B)與收發天線距離建立了線性關系。隨后，以相同的方法來對每個簇第一個時延bin上的歸一化功率增益(A)建模。A和B的表達式給出如下：

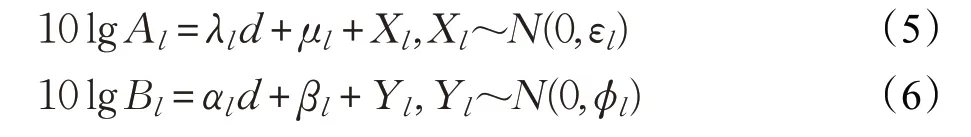
其中，A和B的下標表示第l簇(l=1,2,3)。測量數據和線性擬合函數之間的偏差用零均值的正態分布隨機變量Xl和Yl表示。

3.3 提出模型和仿真流程

考慮到室內樓梯信號的多簇到達特性，本文提出了一種新的隨機多簇信道沖擊響應模型來描述樓梯環境下的無線傳播特性。在LOS 環境下，所提出模型如式（7）所示：

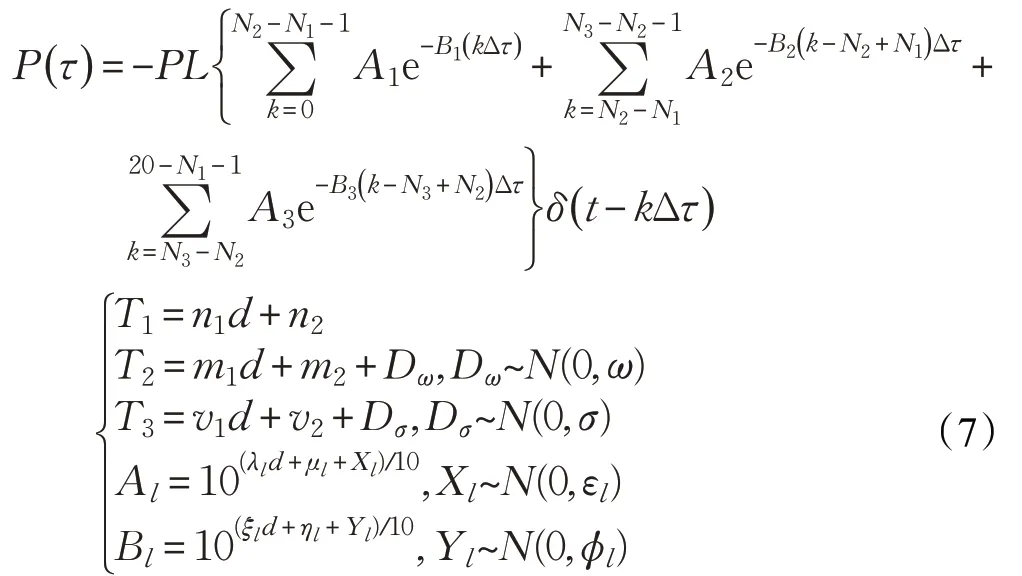
其中，δ(?)是狄拉克函數。

該模型所需參數從大樓東側樓梯提取，具體數值列于表1。此外，圖2 還給出了生成LOS 樓梯CIR 的仿真流程圖。仿真過程將被重復進行500次，然后取平均來獲得某個臺階上的APDP[10]。

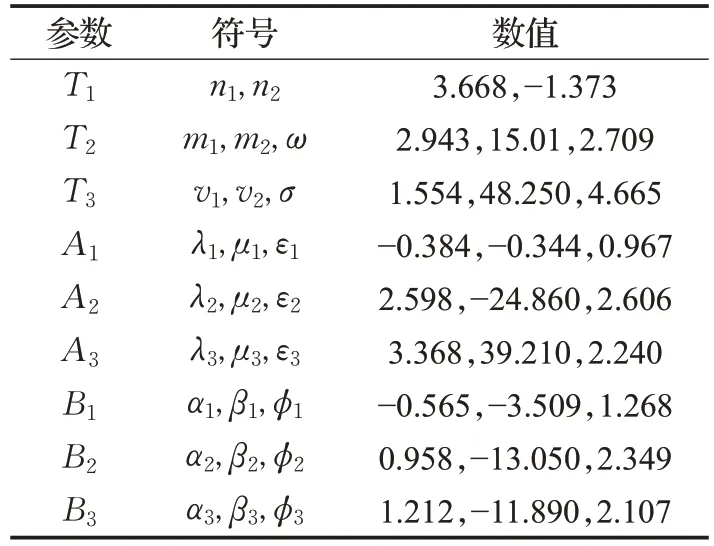
表1 所提出模型參數

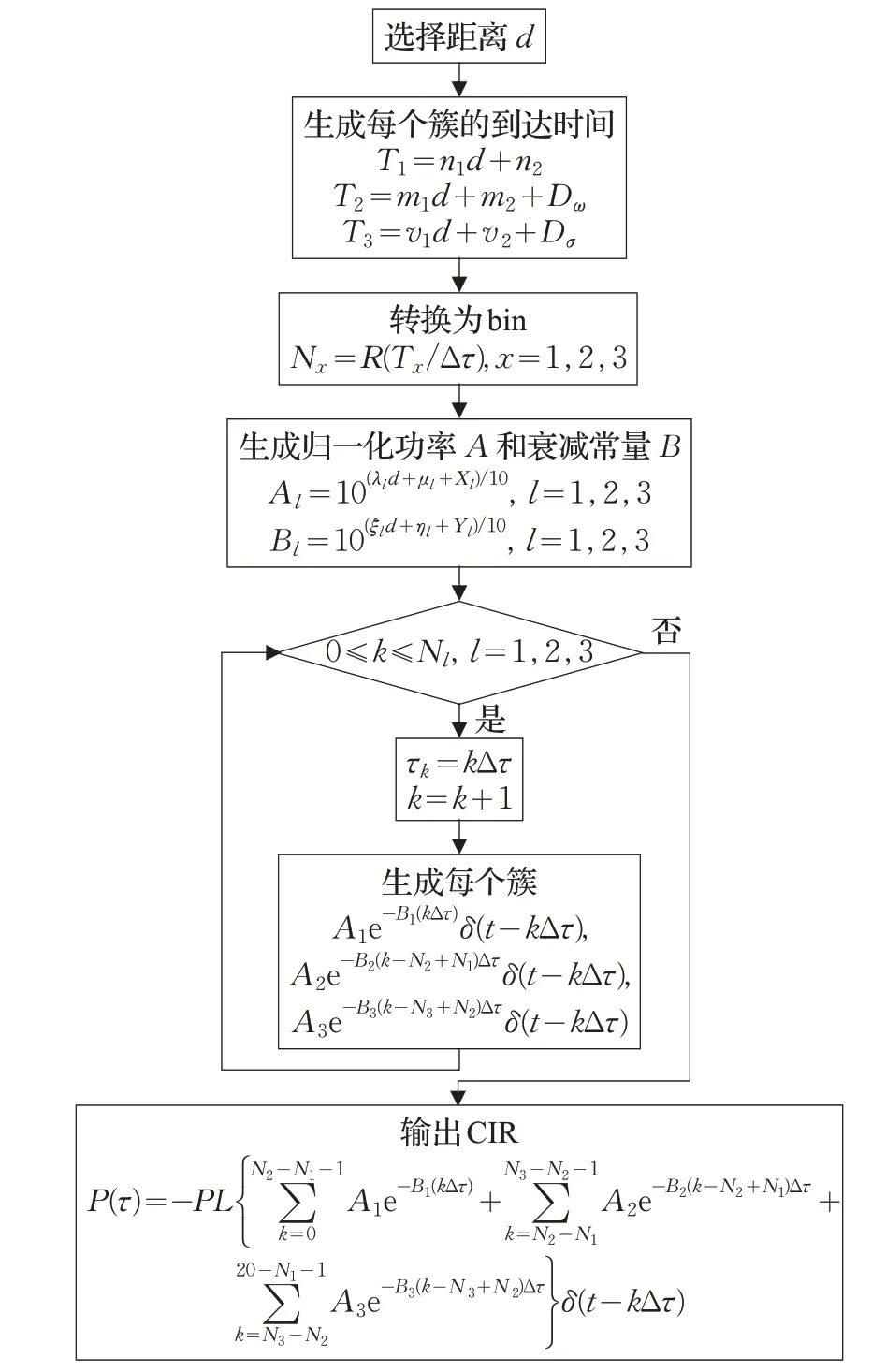
圖2 樓梯環境下生成CIR的仿真流程圖

4 模型驗證

4.1 LOS和NLOS簇到達時間

圖3（a）、（b）、（c）分別給出了LOS 環境下三個簇的到達時間與收發天線距離的線性關系。可以看出，線性函數很好地描述了第一簇到達時間隨距離變化的特性。而反射簇由于傳播路徑的隨機性，線性函數只能描述其變動趨勢。其中，σ值為4.665，較大于ω，這是因為第三簇反射次數更高，傳播路徑的隨機性更大，且傳播路徑更長，受到噪聲干擾的可能性更大。

對于NLOS 樓梯環境，由于橫梁的阻隔，電磁波無法直接到達接收端。此外，信號穿過混凝土材料會發生顯著的衰減[21]。因此對于NLOS功率譜，不考慮直射徑的存在。在NLOS測量實驗中，收發天線之間只存在兩條主要傳播路徑。一條從發射天線所在地板反射而來，另一條來自接收天線周圍墻面。NLOS 下的信號傳播特性與LOS環境較為不同，因而需要重新考慮每個簇的到達時間與距離的相關性。如圖3（d）所示，兩個簇的到達時間弱依賴于收發天線距離。特別的，第一簇總是落在第四個時延bin 內，而第二簇基本上處在第八個時延bin 內。一方面這是由于NLOS 樓梯數據不足，另一方面說明NLOS 下最后六個臺階傳播特性較為相似。在式（7）中的信道建模中，除了需要調整簇的數量以及到達時間，即T1=4Δτ,T2=8Δτ外，其他與LOS環境相同。

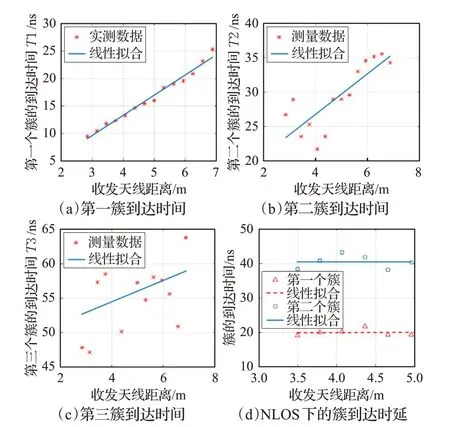
圖3 LOS和NLOS下簇到達時延及相應的線性擬合

4.2 歸一化功率和衰減常量仿真

如圖4和圖5所示，第一簇第一時延bin上的歸一化功率與衰減常量隨著距離的增加而減小，而另外兩個簇呈現相反趨勢。在實際分析中，需要將A1、A2、A3用路徑損耗反歸一化，來研究每個簇第一時延bin 實際的功率增益。事實上，第一簇由直射多徑分量組成，其主要依賴于收發天線距離的變化，因此第一簇第一時延bin上的功率增益(-PL×A1)隨距離增加而減小。此外，B1的趨勢表明，隨著接收天線遠離，隨后到達徑的功率衰減速度將越來越慢。另外兩個反射簇各自第一徑的功率增益(-PL×A2，-PL×A3)幾乎不受距離的影響。這是由于室內樓梯環境下電磁波的波導效應[14，22]。但隨著傳播路徑的不斷增加，反射簇隨后的多徑分量愈難以到達接收端，導致功率衰減速度越來越快。

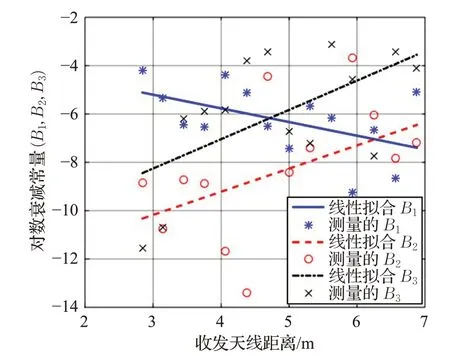
圖4 每個簇的對數衰減常量及相應的線性擬合

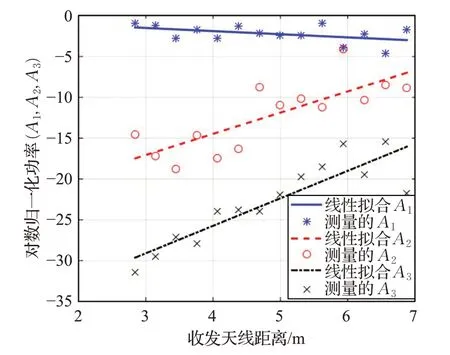
圖5 每個簇的對數歸一化功率及相應的線性擬合

4.3 仿真驗證

在本文中，大樓東側的樓梯用于參數提取，而西側樓梯則用于模型驗證。此外，在模型仿真對比中加入了S-V模型。S-V模型是用于描述信號多簇特性的經典信道模型，此后研究者根據不同帶寬、天線和場景下的實驗結果對S-V 模型進行擴展[23-24]。嚴格來說，這些模型包括S-V 模型在內，其性能并無優劣之分，只有不同的適用場合。

在文獻[12]中，簇和簇內多徑分量的到達時間被描述為不同到達率的雙泊松過程，其衰減常量是通過將一個房間內測得的所有功率譜平均以獲得估計值。這意味著對于一個房間內所有的功率譜，每個簇多徑分量的衰減速度都相同。但是這樣忽略了信號的空間特性，因為即使在同一場景下，不同位置上的信號，其傳播特性也會有所不同，特別是樓梯這樣的周期性結構。

圖6和圖7列舉了接收天線位于Rx1-1和Rx2-6時，所提出模型與測量數據的比較。S-V 模型也包括在圖中，其中LOS 簇和NLOS 簇的到達率分別設為3/100 和2/100。可以清楚看出，所提出模型更適合描述室內樓梯環境下特定接收點的PDP。

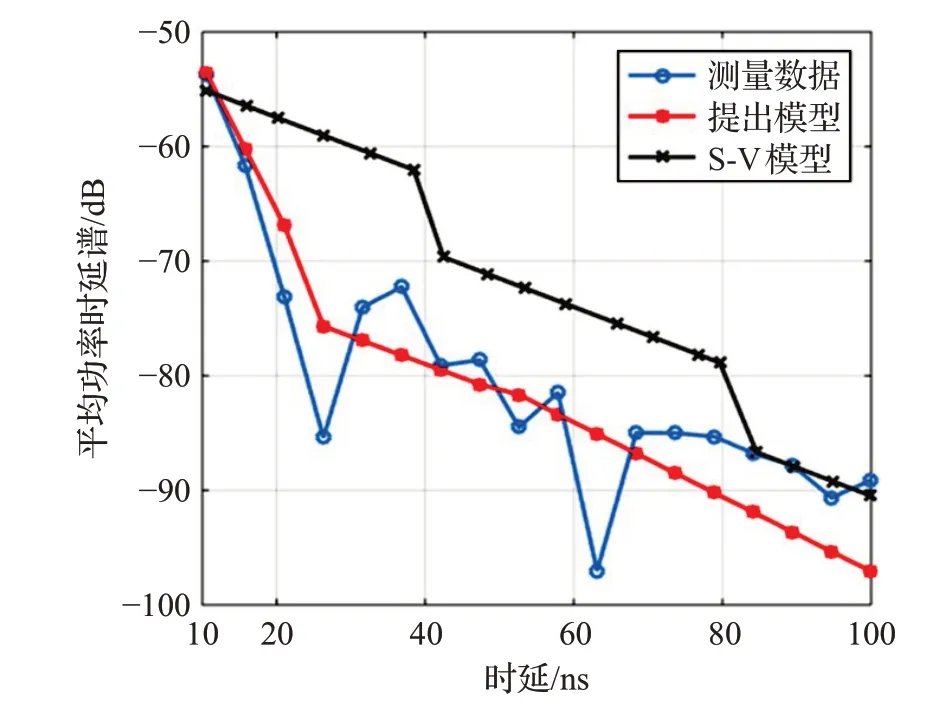
圖6 接收天線Rx1-1處的平均功率時延譜

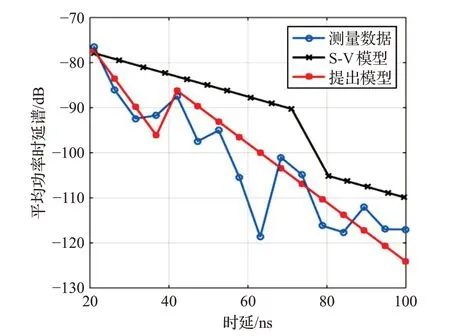
圖7 接收天線Rx2-6處的平均功率時延譜

此外，由式（8）給出的RMS時延擴展[14]將用于進一步模型驗證。RMS 時延擴展通過PDP 計算得來，可以反映出碼間干擾可能性[14]，其中Ak和τk分別為信號的幅度和時延。

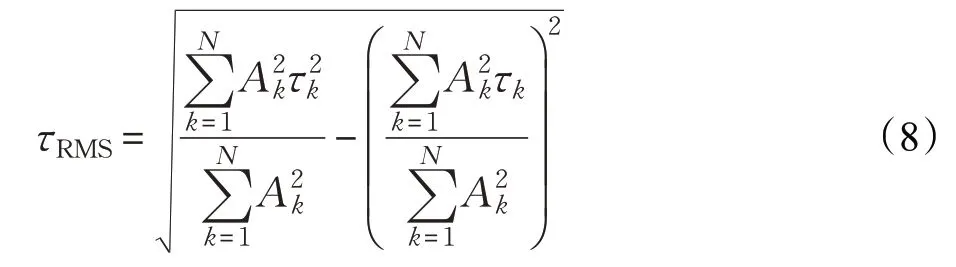
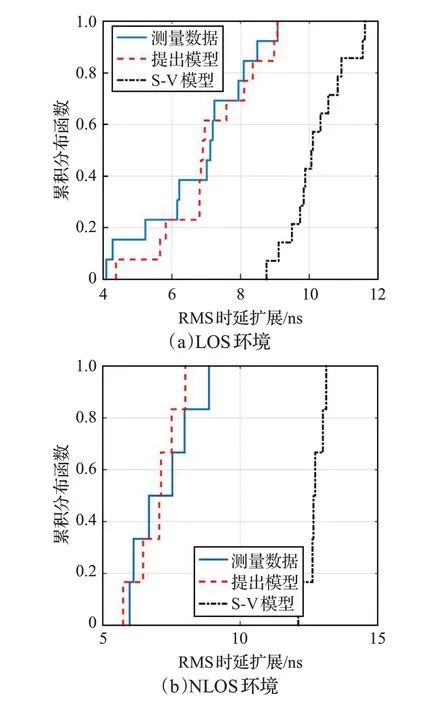
圖8 LOS和NLOS下RMS時延擴展的累積分布函數

圖8 給出了 LOS 和 NLOS 場景下 RMS 時延擴展的累積分布函數（Cumulative Distribution Functions，CDFs）。此外，秩和檢驗被用來確定兩個獨立樣本之間是否存在顯著差異[25]。秩和檢驗的結果總結在表2，其中零假設說明兩個樣本來自同一分布，p表示檢驗統計概率，h是假設檢驗結果的邏輯值。從表2中可以看出，所提出模型均通過了秩和檢驗。而對于S-V模型，h=0，表示零假設被拒絕。

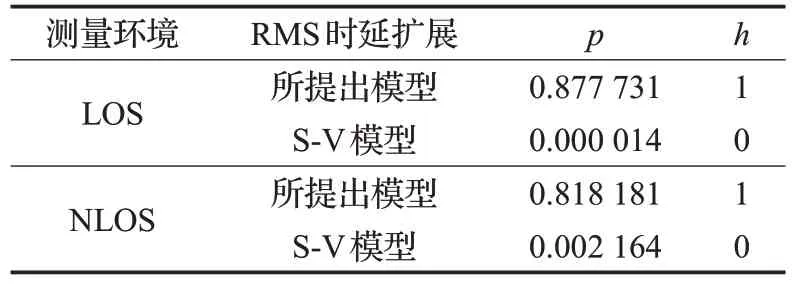
表2 LOS和NLOS環境下秩和檢驗的結果

5 結束語

在LOS樓梯環境下，每個簇的到達時間被建模為距離相關的函數。其中，反射簇的陰影效應用零均值的正態分布隨機變量表示。而在NLOS場景下，簇的到達時間幾乎不受收發天線距離影響。此外，每個簇的多徑分量功率隨時延指數衰減，其衰減常量隨距離變化。

所提出模型的準確性通過廣泛的測量實驗來驗證，并通過APDPs 和RMS 時延擴展進一步評估模型的性能。此外，本文還與經典的S-V模型作客觀比較。秩和檢驗結果表明，所提出的模型通過了零假設，而S-V 模型則拒絕了零假設。相比于S-V模型，所提出的模型更適合描述室內樓梯信號的多簇到達特性。本文所提出的模型可用于應急通信系統的設計，對物理層算法的選擇具有重要意義。