基于FPGA的手寫數字BP神經網絡研究與設計
李增剛,王正彥,孫敬成
青島大學 電子信息學院,山東 青島 266071
1 引言
人工神經網絡在信息處理、人工智能、圖像識別等領域廣泛應用,它是由大量神經元組成的具有復雜運算和監督學習特性的系統。經過70多年專家和學者的努力,神經網絡的結構、算法不斷優化和完善[1]。手寫數字識別是神經網絡重要領域之一,軟件實現神經網絡用數據串行傳送方式,而神經網絡并行傳送數據的特點,正好利用了FPAG數據并行計算和信息實時處理的優點,滿足了工業控制領域對數據實時處理的要求[2]。隨著FPGA技術的發展,集成和內部邏輯單元增多,例如Altera公司生產的FPGA 產品門電路數量有百萬門,集成了PowerPC、Gbits高速乘法單元硬核處理器和MicroBlaze、Picoblaze、Nios 軟核處理器,增強了 FPGA 芯片的處理能力[3]。文獻[3]研究了用平滑插值法在FPGA 上實現BP神經網絡的S型激活函數,并用深度流水線技術實現網絡串并聯。文獻[4]介紹了在FPGA 上對tan-s函數的高精度實現,并用可重構性充分利用FPGA 邏輯資源,對結果進行仿真。文獻[5]介紹了FPGA通過串口與PC機通信,實現圖像卷積處理,利用并行性提升速度,同時減少帶寬和資源的占用。
2 BP神經網絡的原理
BP神經網絡算法由前向運算、誤差反向傳播、權重和偏置更新構成。網絡帶權輸入、激活值、判決輸出是前向運算結果;誤差、梯度、權重和偏置更新在神經網絡反向運算過程[6]。BP算法的流程如圖1所示。
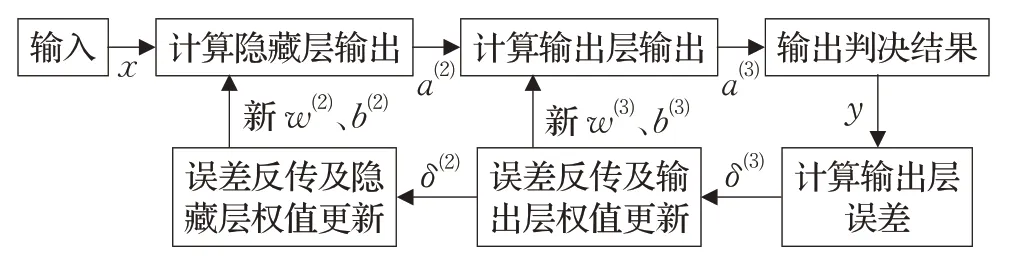
圖1 BP算法的流程示意圖
網絡的前向運算:訓練樣本x根據BP 算法計算網絡隱藏層的a(2)、輸出層的a(3),輸出訓練樣本判決結果y;網絡的反向運算:先計算最后1 層誤差δ(3),計算梯度更新輸出層偏置b(3)、權重w(3),再算前1層誤差δ(2),計算梯度更新隱藏層偏置b(2)、權重w(2),把它們存入存儲器里作為下次訓練樣本的第2、3層網絡權重和偏置。
2.1 BP神經網絡的前向運算
手寫數字BP網絡有輸入層、1個隱藏層和輸出層共3層,輸入層有784個神經元,隱藏層有30個神經元,輸出層有10 個神經元[7],數字像素數據由輸入層傳入,經運算傳給隱藏層,最后由輸出層輸出判決數字0~9。神經網絡第2、3層初始權重和偏置服從均值為0,方差為1的高斯分布。
BP 神經網絡前向運算的第l層的帶權輸入與激活值、權重、偏置的關系式以第2層網絡為例的展開式如下。
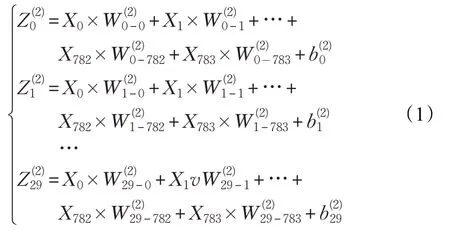
輸入層784 個神經元上的像素數據乘以各自的權重,累乘和傳給隱藏層30個神經元,加上對應的偏置得到第2層神經元的30個帶權輸入,作為S型激活函數自變量算出第2層激活值是第3層網絡輸入數據,計算方法與第2 層網絡相同得到第3 層激活值,網絡最后判決10 個中的最大值,輸出判別數字[8],例如是第3層網絡最大激活值,算法對樣本的識別就是數字6。
2.2 神經網絡的反向運算
神經網絡反向運算是更新權重和偏置,并用MNIST集里測試樣本驗證網絡識別準確率[9]。二次代價函數是找到合適權重和偏置的方法,多次迭代使第3層網絡激活值接近期望值Y,最小化二次代價函數C(w,b)→0 表示BP網絡訓練出合適權重和偏置[10]。為提高網絡訓練速率,隨機選取m個小批量訓練樣本更新網絡權重和偏置,網絡1 次迭代中60 000個訓練樣本使網絡權重和偏置更新60 000/m次。權重和偏置更新公式如下:
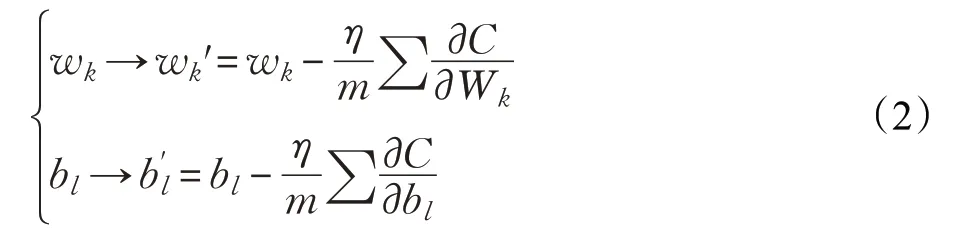
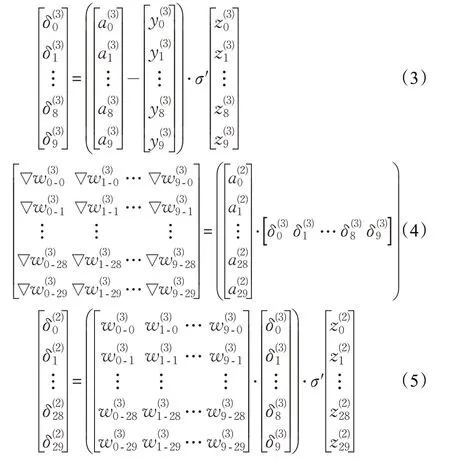
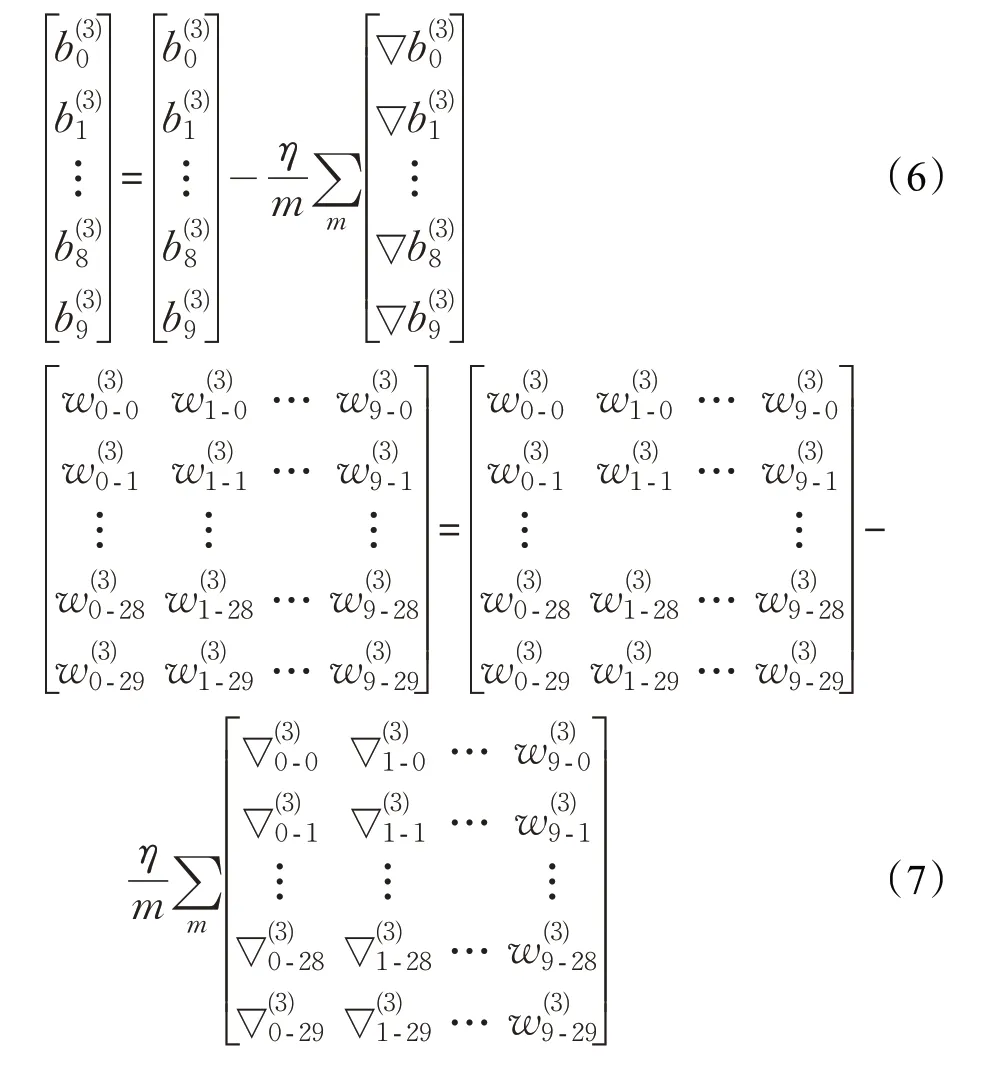
計算網絡誤差是為計算梯度,更新網絡權重和偏置。第3層權重更新公式及展開式(6),第3層偏置更新公式及展開式(7),η網絡學習速率η=3,網絡小批量訓練樣本數m=10 。第2 層權重梯度計算及展開式與第3 層相比只有不同,Xk是訓練樣本784個像素數據。
3 BP神經網絡手寫數字研究
根據python代碼中network庫架構和BP算法原理,用Verilog 語言設計網絡,訓練樣本和網絡權值轉化為S7.12 標準的定點數,其中S 表示符號位,7 表示整數位數,12表示小數位數[11]。另一方面考慮S型激活函數及導數的線性擬合,數據串并行轉化,合理利用邏輯資源[12]。初始權重和偏置放在與.mif關聯的讀寫RAM中。
3.1 神經網絡樣本數據和樣本標簽的寫入
BP網絡MNIST庫60 000個28×28的訓練樣本,圖2是10個手寫數字樣本,像素灰度值范圍0~255[13]。源文件1 個地址數據的高8 位和低8 位各一個樣本像素,每個樣本有自己標簽,用Verilog 語言中的具有讀寫功能的$fopen 函數讀取存放在文本文件中的樣本像素和標簽,在網絡識別與訓練時讀取并寫入樣本存儲器。

圖2 MNIST庫10個手寫數字樣本
3.2 S激活函數σ(z)
BP 神經網絡激活函數是Sigmoid 函數(S 型函數),表達式函數曲線如圖3(a)。Verilog代碼設計采用線性分割擬合S 函數曲線,分段擬合如圖3(b)。表1 是S 型分段函數的浮點數表達式,網絡帶權輸入Z和分段函數系數浮點數轉定點數標準分別是S7.12與S0.12[14]。
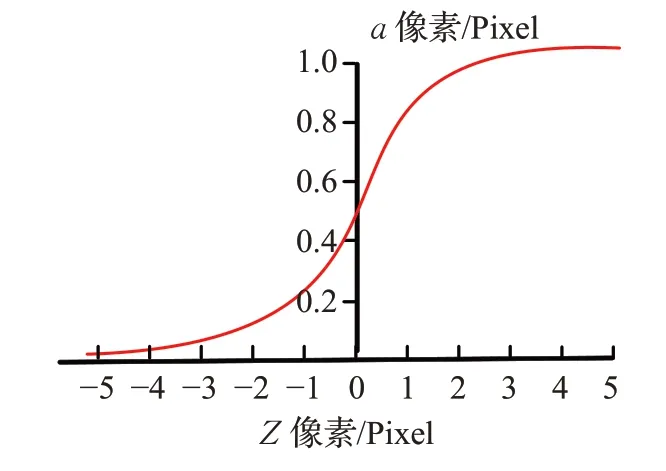
圖3 (a) S型激活函數曲線

圖3 (b) S型激活函數分段曲線

表1 S型分段函數的浮點數表達式
S激活函數線性擬合的定點數Verilog代碼如下:

3.3 S激活函數導數σ'(z)
S函數導數是,函數曲線如圖4(a)。Verilog語言設計σ'(z)函數分段線性擬合曲線如圖4(b)。表2是S函數導數σ'(z)的定點數分段表達式,系數定點數標準是S7.12。
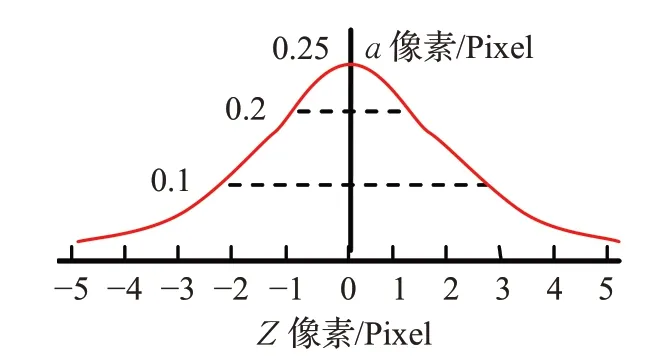
圖4 (a) S型激活函數導數
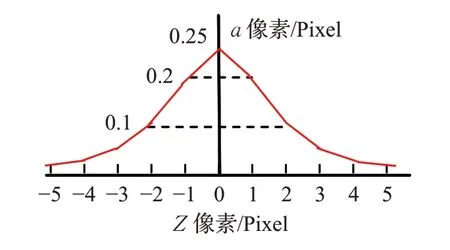
圖4 (b) S型激活函數導數分段曲線
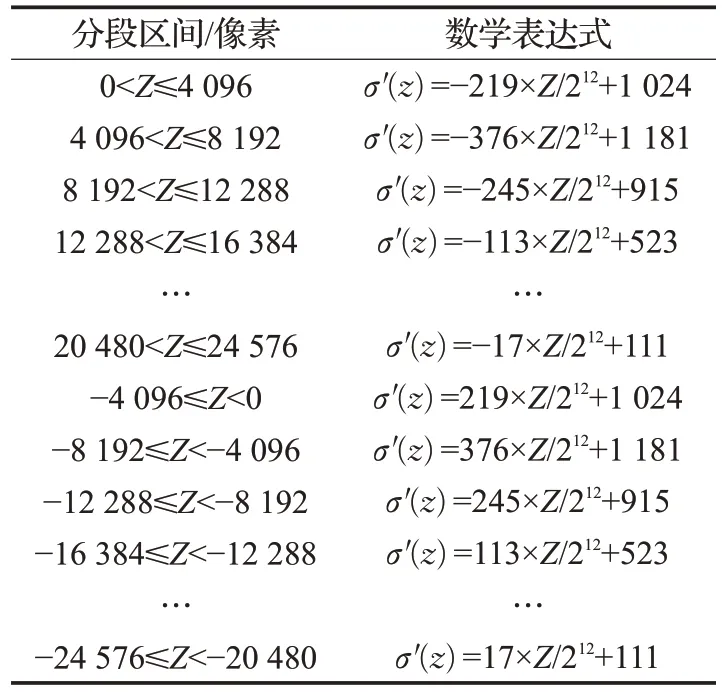
表2 S型導數分段函數的定點數表達式
3.4 BP網絡數據流程
兩個訓練樣本為例的各層網絡信號流程如圖5,包括BP 網絡前向判決輸出和反向計算網絡誤差,1 次權重、偏置的更新[15],設計用的是10個訓練樣本。RAM_x1、RAM_x2是兩個訓練數據存儲器,樣本像素x前向運算傳入第 2 層網絡,z_2_1、z_2_2 是第 2 層網絡 2 樣本的帶權輸入,經過S 型函數算出第2 層網絡2 樣本的激活值a_2_1、a_2_2,根據反向誤差公式第 2 層z_2_1、z_2_2 的導數與第 3 層網絡的誤差e_3_1、e_3_2和權重計算第2層網絡神經元誤差e_2_1、e_2_2,根據式更新偏置并存入偏置存儲器RAM_b2,再根據梯度公式,它與樣本像素x計算第2 層網絡權重梯度g_2_1、g_2_2,根據式更新權重并存入權重存儲器RAM_W2,輸出層的信號流程原理和第2 層網絡相同。z_3_1、z_3_2是第3層網絡帶權輸入,e_3_1、e_3_2是2個樣本第3層網絡誤差,Y1、Y2 是樣本標簽,g_3_1、g_3_2 是2 樣本第3 層網絡權重梯度,RAM_b3 是第3 層網絡的偏置存儲器,RAM_W3是第3層的權重存儲器。根據第2章BP算法公式與BP網絡信號的流程圖設計工程。
3.5 時序設計
在FPGA 平臺上設計手寫數字識別系統,除了BP網絡算法的數學邏輯,還有3 層神經網絡前向、反向運算和網絡神經元權值更新的時序設計。本文采用一個計數器控制3 層網絡的數據存儲器RAM 和神經元誤差、網絡權值梯度狀態[16]。
100 MHz時鐘clk下計數器D計數范圍0~2 455。數值0~786是第2層BP網絡前向運算,787~819是第3層BP網絡前向運算,第2、3層網絡寄存器中帶權輸入導數用于誤差計算,820~851是反向第3層BP網絡計算誤差、梯度和更新權重,884~1 668 是反向運算第2 層BP 網絡誤差、梯度和權重。1 770~2 454是第2組BP網絡訓練的小批量數據,因為RAM關聯的.mif文件是第1組樣本[17]。
4 BP神經網絡手寫數字設計
BP 網絡系統的輸入端口是訓練樣本x1~x10、標簽Y1~Y10 和時鐘clk及復位rst_n,輸出端口是out1~out10樣本判決。圖6是根據第2章BP網絡算法原理,1個樣本判別和權值訓練的電路圖,圖中虛線框是反向運算訓練網絡的權重和偏置。W_RAM2_0~W_RAM2_29為第2層網絡784個地址的權重存儲器,W_RAM3_0~W_RAM3_9為第3層網絡30個地址的權重存儲器,X_RAM為訓練樣本存儲器,b2_RAM為第2 層30 個地址的偏置存儲器,b3_RAM為第3層10個的地址偏置存儲器。
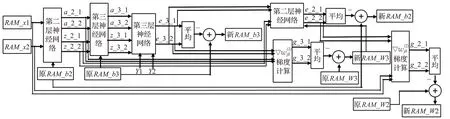
圖5 以2個訓練樣本為例BP神經網絡的前向運算及權重、偏置更新信號流程

圖6 神經網絡前向運算及誤差反饋的電路圖(1個訓練樣本為例)
前向運算的Verilog語言程序(以第2層網絡第1個神經元帶權輸入為例):

存儲器在地址發生器下輸出樣本、權重及偏置,偏置存儲器b_RAM在時鐘clk下串行輸出,進行數據串轉并(每神經元一個偏置)。第2層神經元并行激活值a(l2)轉為串行與第3層神經元權重的累積和計算,最后判決第3 層并行激活值輸出數字[18]。圖7(a)和圖7(b)是神經網絡初始權重和偏置下訓練樣本5前向第2、3層網絡的QuartusII仿真。x[1]是訓練樣本,a3_0~a3_9是第3層神經元的激活值,z_out32是第3個神經元帶權輸入,b32是第3 個神經元的偏置,y_in1 是樣本標簽,out1 是系統判別結果。
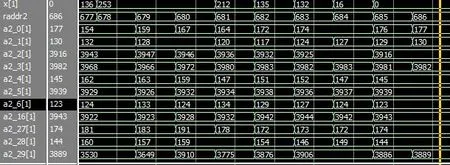
圖7 (a) 激活值a2_0~a2_29的QuartusII仿真
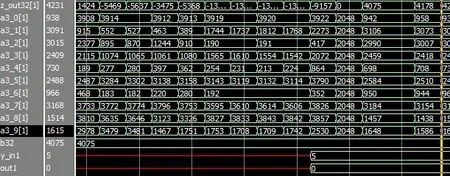
圖7 (b) 識別結果的QuartusII仿真
BP神經網絡的偏置b2串轉并Verilog程序如下(以第2層的30個神經元偏置為例):


BP神經網絡的反向運算式(1)~(3)計算第3層神經元的加權平均誤差(神經元的偏置梯度),更新偏置串行存入b_RAM作為系統下次迭代初始偏置。式(4)和式(7)計算神經元權重的加權平均梯度和更新權重存入W3_RAM。式(5)計算第2 層神經元誤差。最后784 個時鐘clk周期樣本X灰度像素值乘以并行的δ(j2),計算第2層神經元權重的加權平均梯度,更新并存入W2_RAM。至此BP神經網絡完成了1次小批量數據的樣本判別和網絡權重、偏置的訓練[19]。
反向運算Verilog 語言程序(:誤差計算,梯度計算,權值更新):


5 調試結果與分析
本文解決了BP 神經網絡架構架構、MNIST 手寫數字庫、S 型激活函數及導數、各層網絡數據狀態的時序控制、數據串行與并行間轉換、存儲模塊的設計、硬件結構圖。研究手寫數字BP算法,并根據network庫python實現手寫數字的網絡架構[20]。為實現硬件系統,對算法進行相應向量轉換和數據處理,用MNIST 庫60 000 幅手寫數字的像素數據和對應標簽,在FPGA 上實現BP神經網絡的判決和訓練[21],在100 MHz 系統時鐘計算1次迭代耗時150 ms,30次迭代4.5 s,而python2.7軟件在計算機上迭代30次用時329 s,選取第30次迭代的最后1 000 個樣本與標簽,系統記錄判別正確的樣本個數為916 個,即準確率是91.6%,network 庫網絡架構中手寫數字識別率為95.3%。圖8(a)和圖8(b)是網絡中樣本和標簽在QuartusII 13.0 中第1 次迭代的仿真結果。圖中y_in1~y_in10 是神經網絡輸入的小批量數據標簽,out1~out10 是網絡系統的判決,n是系統第n次小批量樣本(60 000個樣本數據,一次讀10個,n最大為6 000),網絡迭代30 次更新權重和偏置。隨機取第1 次迭代n是 4 893 和 5 936 次中的 10 個訓練樣本,n為 4 893 有out3、out6、out8 與out9 和自己對應的標簽不同,n為5 936 有out4、out5 與out10 和自己對應的標簽y_in4、y_in5 與y_in10 不同,驗證網絡識別的準確率增加,第1次迭代識別率為69%(共30次迭代)。
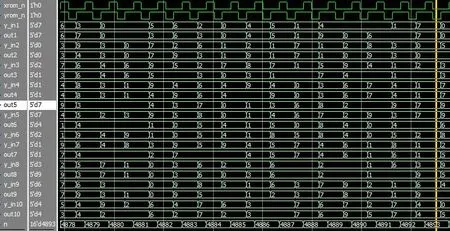
圖8 (a) n=4 893樣本標簽和識別的QuartusII仿真結果
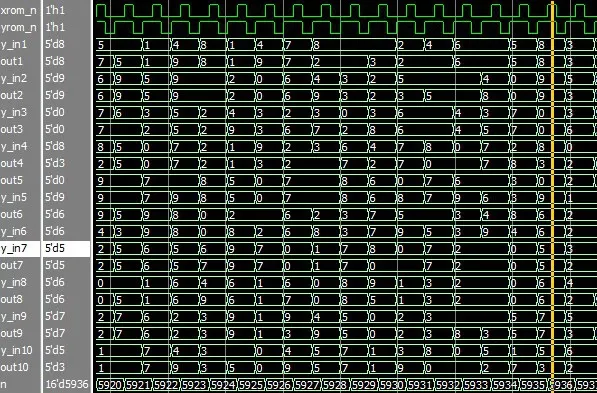
圖8 (b) n=5 936樣本標簽和識別的QuartusII仿真結果
6 結束語
通過仿真與測試分析,網絡系統識別MINST數據庫手寫數字,并能訓練網絡,更新權重和偏置。利用FPGA并行計算實現了硬件速度快的優勢,解決了軟件訓練速度慢、耗時長的問題。該系統可以應用于小型嵌入式數字實時識別,且利用BP 網絡反向訓練及更新權重和偏置,進一步擴展成網絡,為判別其他字符圖片奠定基礎。另一方面FPGA 實現了浮點轉定點和函數線性擬合,降低了數據在BP算法運算中的準確度,可以考慮進一步優化算法和精細劃分S函數及導數擬合區間,提高網絡判決精確度。

