網格法和粒子法模擬齒輪攪油損失中的比較分析
寧 斌,王 斌,呂紅明,王交龍,周雅杰
(1.江蘇大學機械工程學院,江蘇 鎮江 212013)
(2.鹽城工學院機械工程學院,江蘇 鹽城 224051)
(3.鹽城工學院汽車學院,江蘇 鹽城 224051)
網格法是當前處理流體力學問題的常用方法,對于簡單的流動問題能給出準確的結果。網格法指的是在仿真前用若干個子區域來代替原本的計算區域,且每個子區域內的物理量都是由該區域內的節點來決定,通過計算各個節點上的代數方程組來解決流體問題。目前,網格法已經成為研究流體領域問題的主要手段。如彭錢磊等[1]利用網格法對齒輪飛濺潤滑性能進行數值仿真;王斌等[2]利用網格法對漸開線直齒輪在混合潤滑狀態下的效率進行了分析;尹雪梅等[3]在分析油膜軸承壓力分布時采用了動網格技術;Blocken等[4]通過網格法對大氣邊界層進行了CFD模擬。
在處理自由面大變形問題時,網格法很難給出準確的結果。20世紀90年代,MPS法(moving particle semi-implicit method)作為一種無網格法開始受到人們關注[5]。MPS法以Lagrange方程為基礎,用具有密度、速度、動量等物理量的流體粒子代替所要計算的流體域,通過研究流體粒子的情況來觀察整個流域的變化情況。這種方法在解決自由表面發生破碎與翻卷等現象時有很大的優勢。MPS法因為其顯著的優點受到人們的關注,并在許多流體問題中得到應用,如:朱躍等[6]分析了MPS法在多相多組分界面流動的應用;Khayyer等[7]對提高MPS法的穩定性及準確性進行了研究;孫中國等[8]分析了MPS法在流體機械數值模擬中的應用;梁楊楊等[9]采用MPS法對液滴斜向撞擊液面過程進行了數值模擬。
網格法和粒子法都可以用來模擬流體動力學問題,但網格法與MPS法在許多方面存在差異,如前期處理、算法、計算效率等。本文以齒輪攪油模型為例,分別采用網格法和MPS法進行齒輪攪油仿真并對比分析仿真結果與實驗結果,為以后選用分析流體動力學問題的方法提供了參考。
1 數值方法
1.1 控制方程
1.1.1網格法控制方程
網格法中,液體流動問題的控制方程[10]為
(1)
式中:ρ為質量密度;φ為通用物理量;t為空間某時刻;u為質點速度;Γ為速度環量,定義為速度矢量沿封閉曲線的線積分;S為空間內質點或質點域的內能與勢能總和;div為散度函數,反映物理量在各矢量方向上的分散程度;grad為梯度函數。此式為動量守恒方程以及能量守恒方程的通用公式。
1.1.2MPS法控制方程
在MPS法中,基本控制方程主要為Continum方程(質量守恒方程)和Navier-Stokes方程(動量守恒方程),具體方程為:
(2)
(3)
在MPS法中,可以通過對粒子運動情況的分析,獲得整個流體域的運動狀況。在運動過程中,各個粒子都會對相鄰粒子產生作用,對于粒子間相互作用,主要采用權函數[11]進行計算。
(4)
式中:W(r)表示粒子間的相互作用;r為粒子間的距離;re為粒子作用半徑。
從式(4)可知:當r 1.2.1SIMPLE算法 本文選用網格計算方法中最為普遍的SIMPLE[12]算法。它是一種半隱式算法,通過壓力修正理論對方程進行迭代求解,并使用上一次的迭代結果構建下一次的迭代,主要計算流程為: 1)設定壓力值P*(P*為任意值)。 2)將P*與動量方程相結合,求解速度場,u*,v*,w*表示速度分量。 3)由于P*為空間某時刻的任意值,因此一般情況下通過動量方程獲得的速度矢量u*也為任意值,即與周圍空間點存在速度梯度誤差,所以此時獲得的速度場不滿足連續方程,需要構建壓力修正值P′,P′和P*相加后就可得到準確的壓力值P,P=P′+P*。 4)通過P可以獲得更加準確的速度場u,v,w(符合連續方程)。 5)將P設為新預測值P*,重新開始迭代計算。 1.2.2時間積分法 MPS法通過半隱式的時間積分法來解決問題,該算法與SIMPLE算法一樣,主要用來解決不可壓縮流體的問題。時間積分法求解過程包含兩步:顯式修正和隱式修正。具體計算流程如下: (5) (6) 2)通過計算Poisson方程,得到下一時刻的壓力; (7) 3)由所獲得的壓力,獲得該時刻的粒子速度及位置: (8) (9) 1.3.1邊界層理論 網格法中,流體的控制方程為非線性方程,這使得邊界問題很難處理。本文以齒輪攪油為模型,在攪油過程中,油液在箱體壁面以及齒輪表面產生湍流。湍流區可以分為與箱體壁相互作用的近壁區和遠離箱體壁的完全湍流區。由于受到箱體壁的影響,油液在近壁區的流動與在完全湍流區的流動有較大差異。根據與箱體壁的垂直距離,將近壁區劃分為3個子層,依次為黏性底層、過渡層以及對數率層,各子層高度和速度如下: (10) (11) 1.3.2MPS法邊界處理方法 在MPS法中,流體粒子在邊界處易發生粒子缺失以及粒子穿透的現象,這樣將無法保證仿真結果的準確性。本文通過在邊界處以及邊界外布置多層邊界粒子[13]來防止這類現象的發生。由圖1可知,邊界粒子分為2類:第一類為與流體接觸的壁面粒子,這一類粒子主要分布在固壁上的壁面粒子;第二類為分布在邊界外的壁外粒子。在計算過程中,采用權函數(式(4))計算壁面粒子與流體粒子。若計算時不考慮壁外粒子,一方面會使得壁面粒子被認定為流體粒子,另一方面會使計算所得的粒子密度小于實際值,所以需要在邊界外分布多層粒子,壁外粒子的層數由權函數中re的大小決定。 圖1 壁面邊界的粒子分布 在求解過程中,為了防止粒子在與壁面接觸后穿過邊界,需要計算壁面粒子的壓力,這樣能夠確保液體粒子撞到壁面后能夠回彈。 本文分別采用網格法與MPS法進行齒輪攪油仿真,并對仿真結果進行比較分析。首先齒輪攪油模型是一個流體領域的典型案例,其次齒輪攪油損失是測量電動汽車減速箱功耗的重要參考指標,具有實際意義。不僅如此,在齒輪嚙合轉動過程中,油液面會發生較大的變形,尤其是當油液撞擊到箱體壁后,液面會發生翻卷、破碎等自由面流動現象。因此分別用網格法和MPS法對齒輪攪油模型進行數值仿真并比較獲得的仿真結果,具有一定的參考價值與研究意義。 建立NX攪油齒輪箱模型,如圖2所示。一對嚙合齒輪安裝在箱體中間,將油液倒入箱體內,油液寬度L=360 mm,高度H=145 mm,油液面與齒輪中心在同一水平面,箱體容積為360 mm×290 mm×100 mm。表1為齒輪副基本參數,其中主動輪為G1、從動輪為G2。 表1 齒輪副基本參數 圖2 攪油模型幾何尺寸 2.2.1網格法前期處理 在使用網格法進行仿真前要對模型進行網格劃分,由于齒槽間的間隙過小,使得在嚙合區域所劃分的網格質量較差,會對仿真結果產生影響,因此本文將兩個齒輪分別向兩側移動1 mm,增加嚙合區域間隙,從而確保網格的質量。 在求解過程中,模型的網格數越少,則求解速度越快。本文通過局部加密法來劃分網格,對輪齒周圍區域進行加密,并在齒槽區域劃分雙層網格,這樣能夠減少求解時間、提高仿真準確性,局部網格加密圖如圖3所示[14]。 圖3 局部網格加密圖 隨后將劃分好的網格模型導入仿真軟件內,采用壓力基求解,如圖4所示。由于齒輪在轉動時,流體會產生劇烈飛濺,油液面無法確定,因此由流體單元網格與總體積比函數F來確定自由面。 圖4 VOF兩相流設置 2.2.2MPS法前期處理 分別定義箱體、油液和齒輪3個部分的物理屬性,如圖5所示,將油液的物理屬性定義為Fluid(流體),齒輪組與箱體的物理屬性定義為Polygon(多面體)。Fluid為MPS法仿真軟件中最為重要的元素,由粒子充當流體的角色,可以定義流體密度、運動黏度等物理量。而Polygon為盛放液體的容器,以自身輪廓為邊界條件,表達液體和粒子的接觸。 圖5 定義各組件物理屬性 本文分別采用ANSYS[14]和Particleworks兩種軟件對齒輪攪油進行模擬仿真。如圖6所示,初始時,齒輪副未開始轉動,油液處于靜平衡狀態,在t=0時,主動輪G1開始轉動,通過齒輪副的轉動帶動油液的運動。在計算前,將壓力分布設置為靜壓,油液密度ρ0=900 kg/m3,重力加速度g=9.8 m/s2,運動黏度系數υ=1.82×10-4m2/s。 圖6 初始油液位置 圖7與圖8顯示的是齒輪副剛開始轉動和油液開始翻卷的典型時刻的仿真圖像。通過油液的分布狀況可以看出,盡管流場變化比較劇烈,液面發生了翻卷,但網格法與MPS法均能很好地捕捉到這些特征。 圖7 齒輪轉動0.01 s時流域仿真圖 圖8 齒輪轉動0.1 s時流域仿真圖 從細節上看,網格法與MPS法存在著一些差別,如圖7所示,在0.01 s仿真剛開始時,在網格法中自由面變化并不是很劇烈,但在粒子法仿真中能夠清楚地看出一些油液粒子運動較為劇烈,這種現象在齒輪轉動0.1 s后更為明顯(圖8)。這主要是由于MPS采用了式(4)的權函數,當相鄰的粒子在靠近時,粒子數的密度快速增加,使得粒子飛濺。 為了比較網格法與MPS法對于齒輪攪油的準確性,用上述攪油模型進行實驗,并將實驗數據與數值仿真獲得的數據進行比較,圖9、圖10為在不同轉速與轉向情況下,齒輪副攪油損失變化曲線和數據點。由圖可知,網格法與粒子法的計算結果逐漸收斂于相近的結果。由于實驗測量時存在著裝配誤差、傳感器測量誤差以及其他一些不可控因素,而仿真數據是理想狀態下的齒輪攪油功耗,因此兩者之間存在一些偏差,但誤差大小仍在允許范圍內。 圖10 攪油功率損失(主動輪順時針轉動) 圖9 攪油功率損失(主動輪逆時針轉動) 因為網格法和MPS法采用不同的算法,所以在計算效率方面同樣存在一定的差異。在網格法中,大量的時間會花費在網格劃分中,且網格的質量在很大程度上影響計算的效率和精度。在MPS法中粒子的大小也會影響計算的效率和精度。為了能夠準確地比較兩類方法的計算效率,本文通過對網格的大小與粒子的大小進行控制,使網格的體積與粒子的體積接近,由此對比在網格體積與例子體積接近時兩類方法的計算效率。本文中最大網格體體積約為7.78×10-8m3,最小網格體體積約為3.93×10-12m3。因此本文設粒子的直徑為1 mm,則每個粒子體積約為4.19×10-9m3,處于最大網格體積與最小網格體積之間。計算時使用相同的時間步長1×10-4s。 經比較,MPS法的計算時間約為網格法的三分之一。由此可得,MPS法在計算效率上有較大優勢。 在計算精度方面,由于網格法軟件的限制,本文將齒輪嚙合間隙有意擴大了2 mm,加大了齒輪嚙合時的空隙和嚙合齒輪之間的泵油量,使得齒輪間泵油損失增加,在一定程度上降低了計算的準確性。由此可知,MPS法在計算精度上具有一定的優勢。 本文通過網格法與MPS法分別對齒輪攪油進行了數值模擬和比較分析,結論如下: 1)在仿真結果方面,網格法和MPS法均能捕捉到齒輪轉動時的自由液面的變化狀況,說明兩種方法都能準確地解決流體動力學方面的問題。 2)在計算攪油損失結果方面,兩種方法所計算的結果與實驗結果相吻合。 3)在計算效率方面,本文通過控制網格和粒子的體積大小來比較兩者的計算效率,使得MPS法的計算效率明顯高于網格法。 4)在計算精度方面,由于網格法在進行網格劃分前需擴大齒輪間隙,降低了困油區的密閉性,使得攪油時的泵油量高于實際值;而MPS法則完全模擬真實攪油狀態,相對計算精度較高。1.2 算法的選用比較
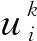
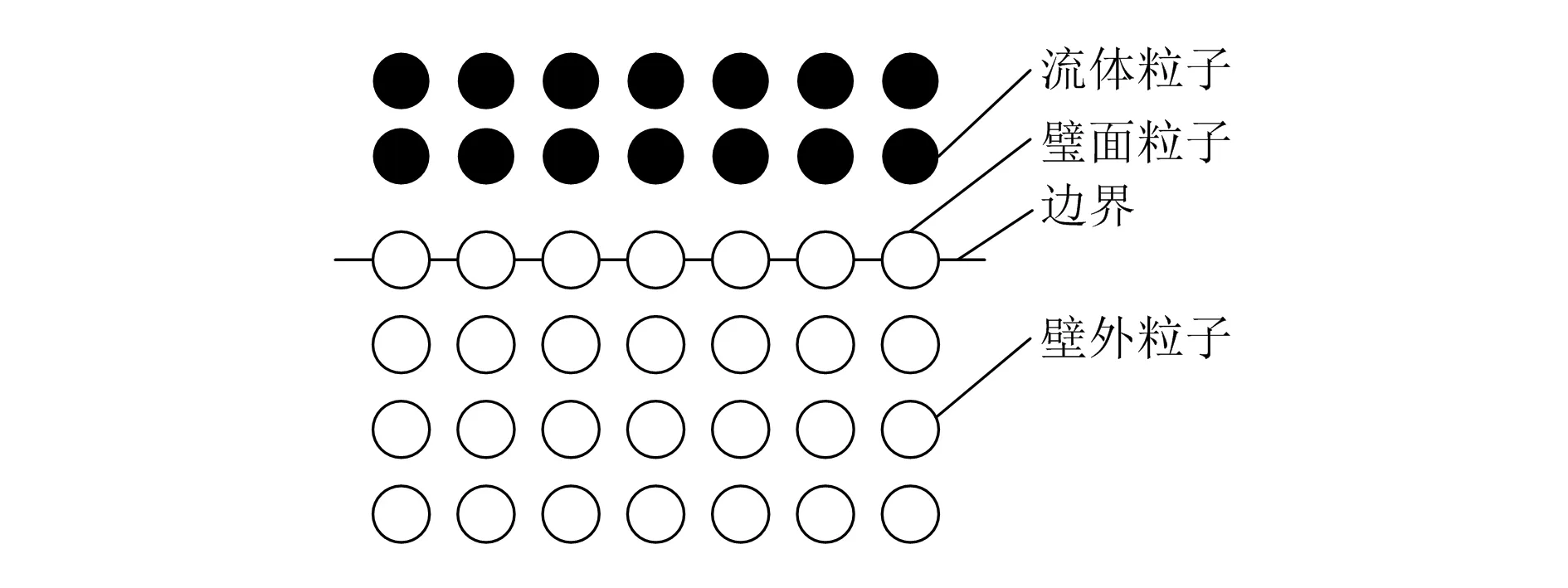
1.3 邊界處理方式比較
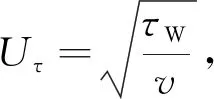
2 仿真過程與結果比較分析
2.1 建立攪油模型

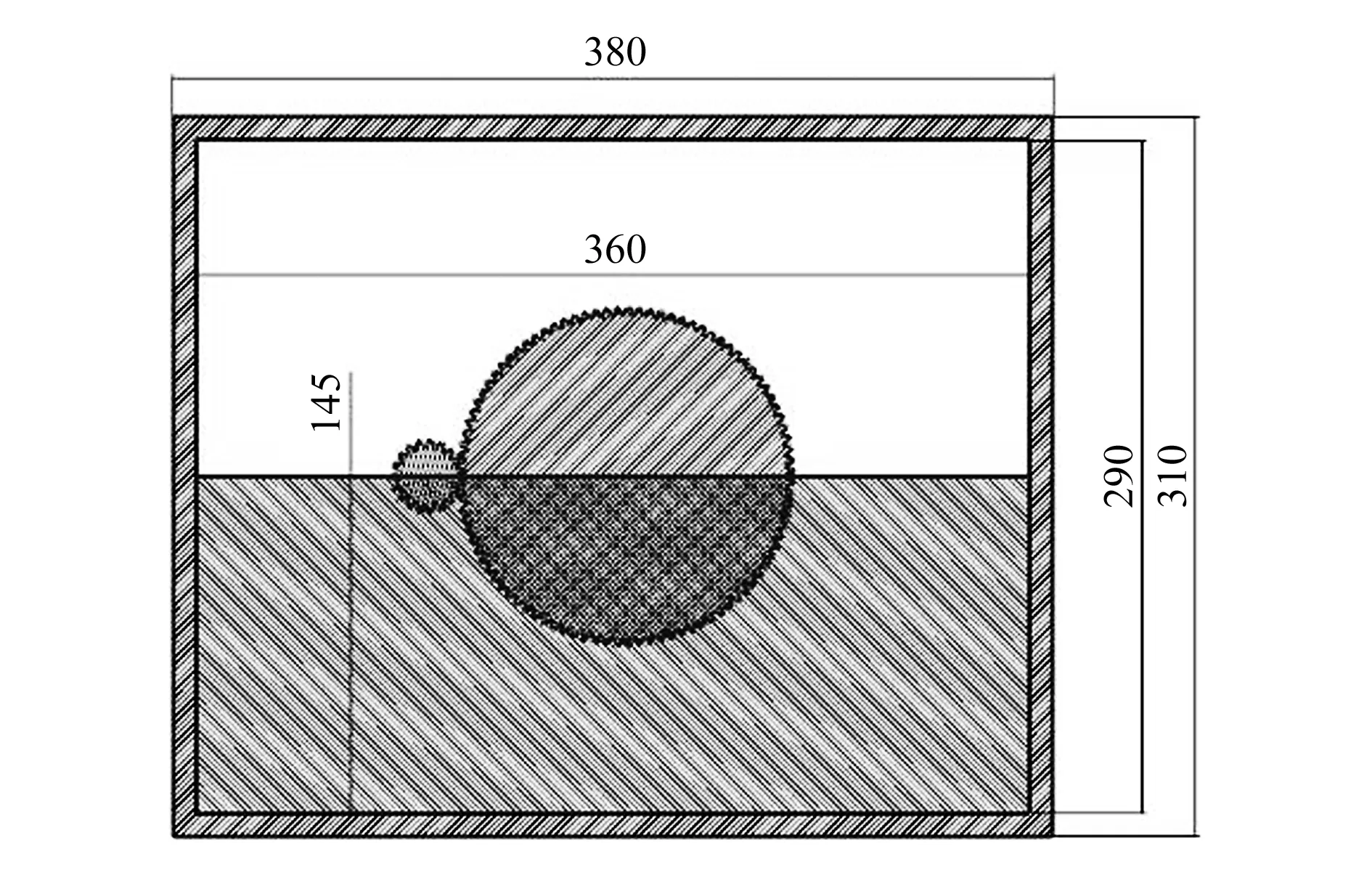
2.2 前期處理比較

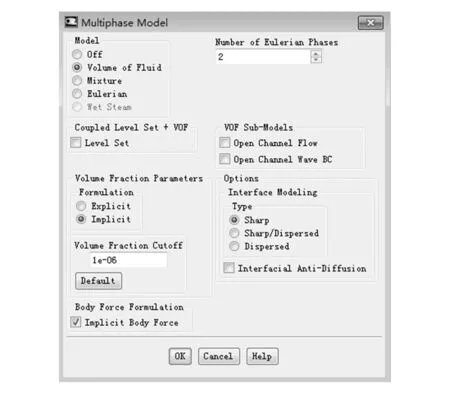
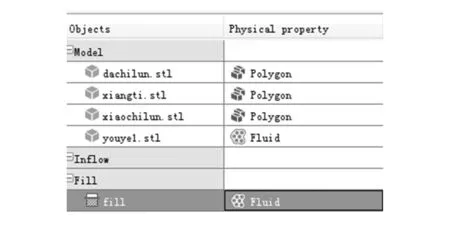
2.3 仿真結果比較
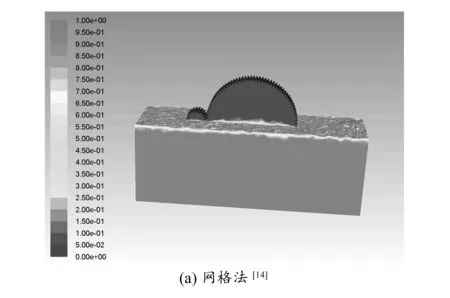
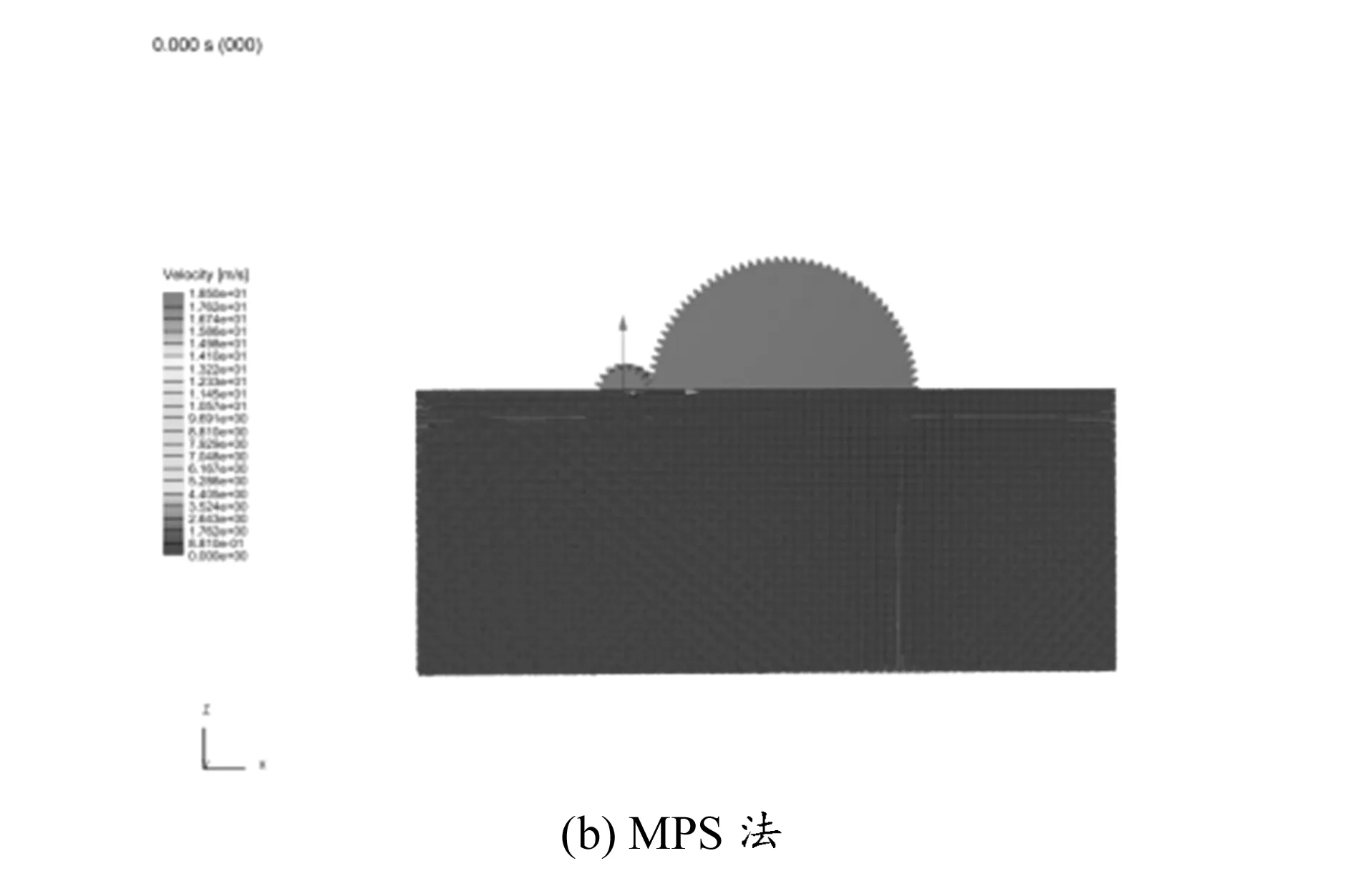


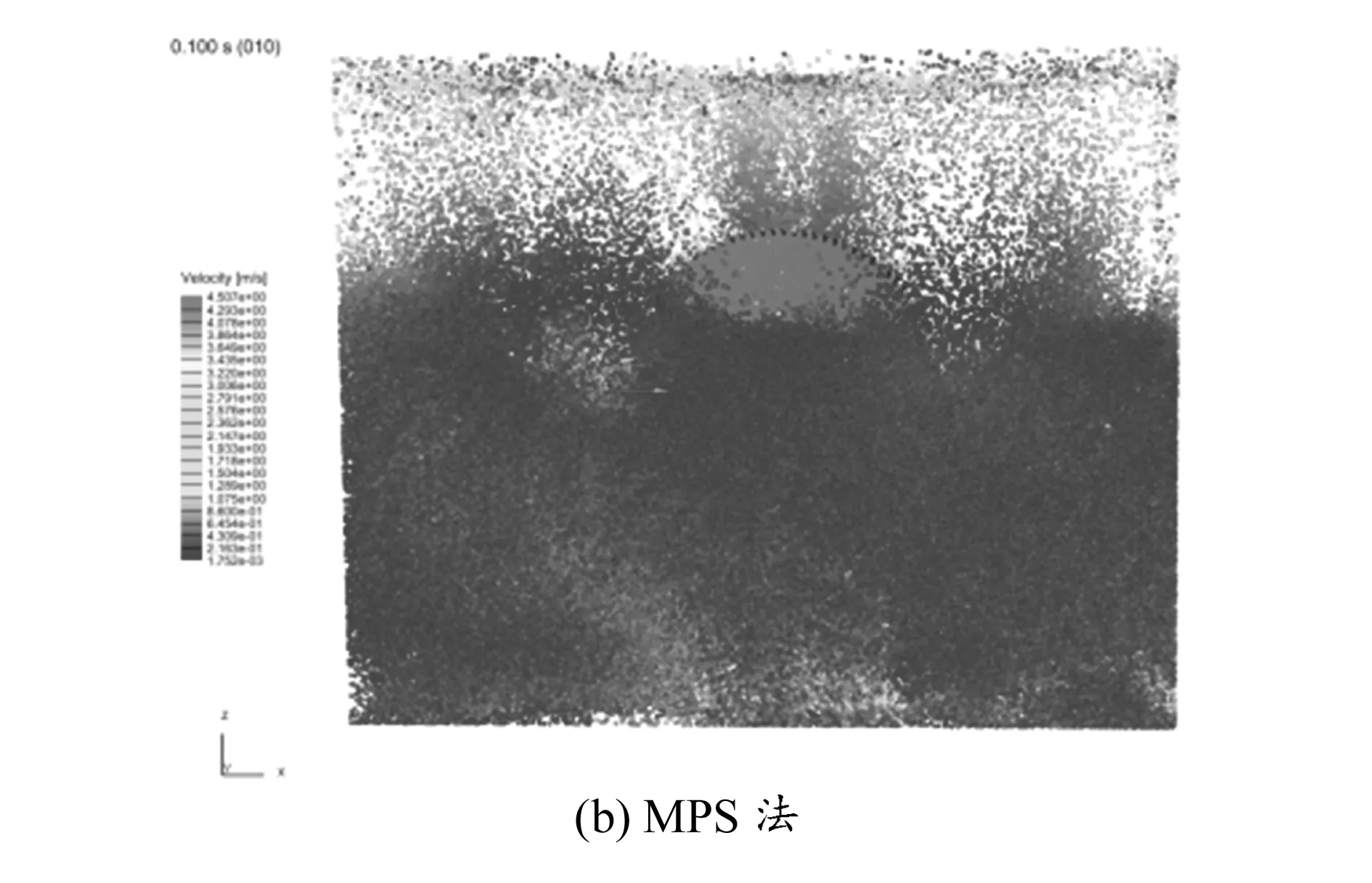
2.4 數值結果比較
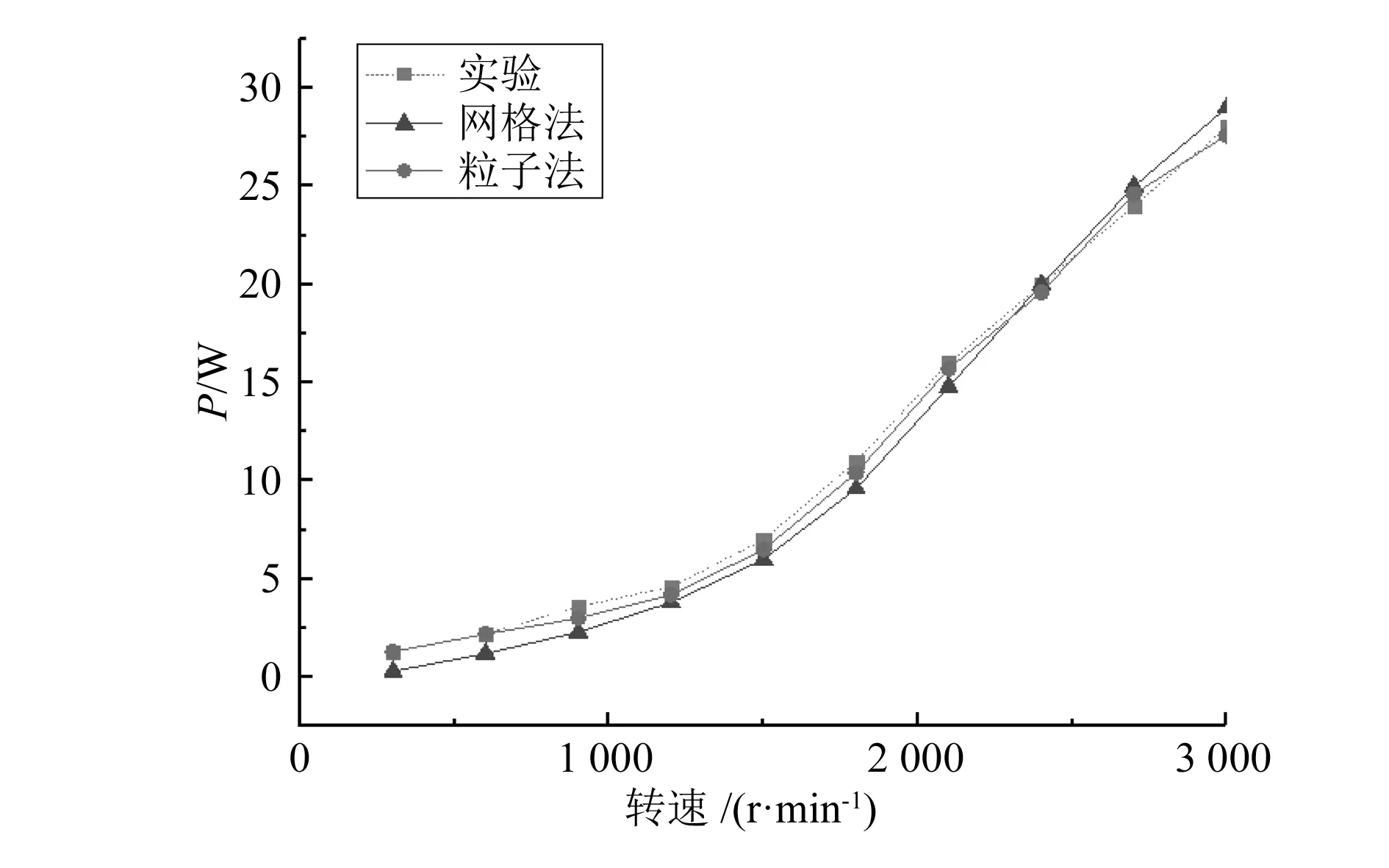

2.5 計算效率及精度的比較
3 結論

